前言
这两天接了个简单的活,关于设计一个Sallen-Key二阶低通滤波器,有一些体会。
1 Sallen-Key二阶低通滤波器结构
这个结构很简单,优势就是在于简易实现二阶低通。这种类电压跟随器的结构,其增益为1。

2 截止频率
在网上可以查到,该结构截止频率为:

然而,在仿真中,当选定Ra=Rb,Ca=Cb时就会发现,-3dB的衰减频率点并非我计算得到的截止频率数值。然而中心频率却是对应计算得到截止频率。
网络上也存在特征频率和截止频率的区别的相关说明,二阶的计算也有,不过是针对于纯RC电路的。
这里给出下计算截止频率为10kHz下的仿真图和交流分析结果:
 

 可以发现,10KHz时,衰减明显大于10KHz,相位的中心频率-90°点在10KHz处。因此设定的电阻电容值对应的截止频率并非10KHz。
可以发现,10KHz时,衰减明显大于10KHz,相位的中心频率-90°点在10KHz处。因此设定的电阻电容值对应的截止频率并非10KHz。
那么问题来了,哪儿出现了问题。
为此我查阅了很多资料,发现当取Ra=Rb,设定Cb如下:

那么Ca的计算就可以等效为:
 值得一提的是,这里的计算截止频率的方式还是前面提到的公式,只是不取Ca=Cb。此时仿真和交流分析结果如下:
值得一提的是,这里的计算截止频率的方式还是前面提到的公式,只是不取Ca=Cb。此时仿真和交流分析结果如下:

 可以发现,中心频率依旧在-90°,当时幅值响应中10KHz的衰减明显接近于-3dB,下图为局部放大: 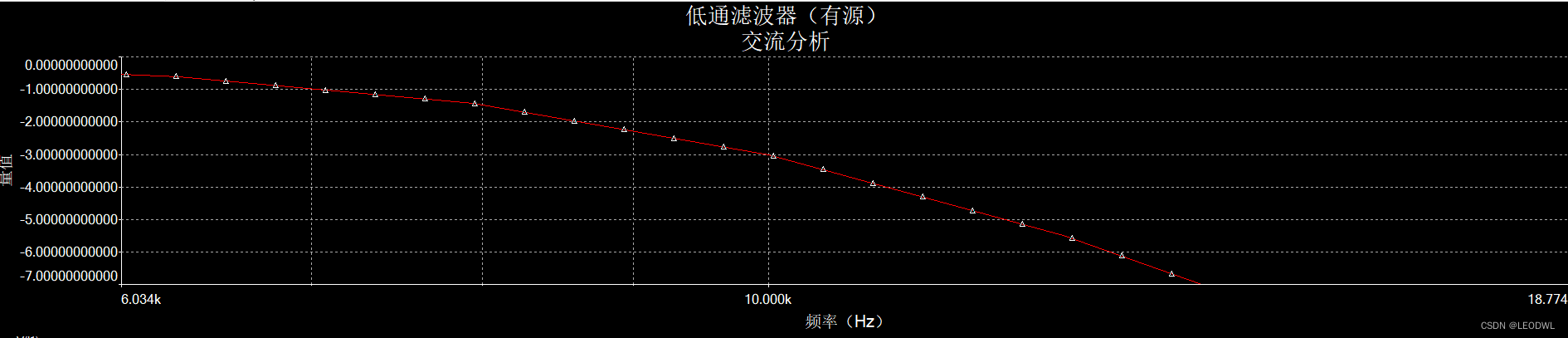 由放大图可以看到,10KHz处的幅值准确的位于-3dB处。
可以发现,中心频率依旧在-90°,当时幅值响应中10KHz的衰减明显接近于-3dB,下图为局部放大:  由放大图可以看到,10KHz处的幅值准确的位于-3dB处。
3 结语
Sallen-Key滤波是一种基于运算放大器阶段简单的有源滤波器,它是理想的过滤音频频率。
这是一种最广泛使用的滤波器拓扑结构。其受欢迎的原因之一是,这种配置对运算放大器的性能的过滤器性能的依赖性最小。这种结构的另一个优势是,最大电阻值最小的电阻值和电容值的最大最小电容值的比例很低。
然而,其一个严重的缺点是不易调谐滤波。因此电容的选取是很有可能影响其调谐频率的,此时的相位中心频率却不会为此而改变。
本博客讲的也多是实践中遇到的问题,由于自身并非从事这个方向,对于细节的东西也没有过多的把握,不过相关的参数设计肯定是存在规律和方式的,只不过过程相比于普通的RC滤波显然会更加复杂,简单的结构往往也会带来复杂的设计过程,所以鱼和熊掌一般不能兼得。
对参数设计有兴趣的可以参考卓晴老师的博客,写的很好:Sallen-Key 低通滤波器设计过程








 文章探讨了Sallen-Key二阶低通滤波器的结构和设计问题,特别是在截止频率计算与实际仿真结果的差异。作者通过调整电阻电容值发现,当Ra=Rb,Ca=Cb时,-3dB衰减频率并不等于理论计算的截止频率。通过调整Ca和Cb的比例,可以更准确地控制滤波器在10kHz处达到-3dB衰减。文章强调了滤波器设计的复杂性和电容选择对调谐频率的影响。
文章探讨了Sallen-Key二阶低通滤波器的结构和设计问题,特别是在截止频率计算与实际仿真结果的差异。作者通过调整电阻电容值发现,当Ra=Rb,Ca=Cb时,-3dB衰减频率并不等于理论计算的截止频率。通过调整Ca和Cb的比例,可以更准确地控制滤波器在10kHz处达到-3dB衰减。文章强调了滤波器设计的复杂性和电容选择对调谐频率的影响。


















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










