四元数
四元数的定义是 [ w ( x y z ) ] = [ c o s ( θ / 2 ) ( s i n ( θ / 2 ) n x s i n ( θ / 2 ) n z s i n ( θ / 2 ) n z ) ] [w\quad(x\quad y\quad z)]=[cos(\theta/2)\quad (sin(\theta/2)n_x\quad sin(\theta/2)n_z\quad sin(\theta/2)n_z)] [w(xyz)]=[cos(θ/2)(sin(θ/2)nxsin(θ/2)nzsin(θ/2)nz)]
四元数满足结合律但是不满足交换律:
(
a
b
)
c
=
a
(
b
c
)
a
b
≠
b
a
(ab)c=a(bc)\\ ab\neq ba
(ab)c=a(bc)ab=ba
两个四元数模的积满足
∥
q
1
q
2
∥
=
∥
q
1
∥
∥
q
2
∥
\left \| q_1q_2\right \|=\left \| q_1\right \|\left \| q_2\right \|
∥q1q2∥=∥q1∥∥q2∥
四元数的逆和矩阵的逆类似
(
a
b
)
−
1
=
b
−
1
a
−
1
=
(
q
1
q
2
.
.
.
q
n
−
1
q
n
)
−
1
=
q
n
−
1
q
n
−
1
−
1
.
,
.
q
2
−
1
q
1
−
1
(ab)^{-1}=b^{-1}a^{-1}= (q_1q_2...q_{n-1}q_n)^{-1}=q_n^{-1}q_{n-1}^{-1}.,.q_2^{-1}q_1^{-1}
(ab)−1=b−1a−1=(q1q2...qn−1qn)−1=qn−1qn−1−1.,.q2−1q1−1
利用这些性质,我们可以对四元数
p
p
p向任意表示旋转方向的单位向量
n
^
\hat{n}
n^旋转表示成四元数之间的乘积
q
′
=
q
p
q
−
1
{q}'=qpq^{-1}
q′=qpq−1
其中
q
=
[
c
o
s
θ
/
2
,
n
^
s
i
n
θ
/
2
]
q=[cos\theta/2,\hat{n}sin\theta/2]
q=[cosθ/2,n^sinθ/2]。特别地,
p
p
p先向四元数
a
a
a映射在三维空间的方向旋转再向四元数
b
b
b映射在三维空间的方向旋转等于向四元数
b
a
ba
ba映射在三维空间的方向上旋转,这个方向就是它们各自
n
^
\hat{n}
n^在三维空间的方向:
p
′
=
b
(
a
p
a
−
1
)
b
−
1
=
(
b
a
)
p
(
a
−
1
b
−
1
)
=
(
b
a
)
p
(
b
a
)
−
1
p^{'}=b(apa^{-1})b^{-1}\\ =(ba)p(a^{-1}b^{-1})\\ =(ba)p(ba)^{-1}
p′=b(apa−1)b−1=(ba)p(a−1b−1)=(ba)p(ba)−1
四元数对log的定义为
l
o
g
q
=
l
o
g
(
[
c
o
s
α
n
^
s
i
n
α
]
)
=
[
0
α
s
i
n
α
]
log^{q}=log([cos\alpha\quad \hat{n}sin\alpha])=[0\quad \alpha sin\alpha]
logq=log([cosαn^sinα])=[0αsinα]
四元数对exp的定义为
e
x
p
(
p
)
=
e
x
p
(
[
0
α
n
^
]
)
=
[
c
o
s
α
n
^
s
i
n
α
]
exp(p)=exp([0\quad \alpha \hat{n}])=[cos\alpha\quad \hat{n}sin\alpha]
exp(p)=exp([0αn^])=[cosαn^sinα]
从而有
e
x
p
(
l
o
g
q
)
=
q
exp(log^{q})=q
exp(logq)=q
以四元数
q
q
q为底的指数
q
t
q^{t}
qt相当于随t从0到1对单位四元数到四元数q旋转的插值而单位四元数定义为
[
1
0
]
[1\quad 0]
[10]或
[
−
1
0
]
[-1\quad 0]
[−10]
代码调式如下:
//Quaternion (input and output)
float w,x,y,z;
//Input exponent
float exponent;
//Check for the case of an Identity quaternion,this will protect against divide by zero
if(fabs(w)<.9999f)
{
float alpha = acos(w);
float newAlpha = alpha * exponent;
w=cos(newAlpha);
float mult=sin(newAlpha)/sin(alpha);
x*=mult;
y*=mult;
z*=mult;
}
如果以四元数 q 0 q_{0} q0到四元数 q 1 q_{1} q1平滑过渡的旋转,则要使用以下代码
float w0,x0,y0,z0;
float w1,x1,y1,z1;
//The interpolation parameter
float t;
float w,x,y,z;
//output quaternion
float cosOmega=w0*w1+x0*x1+y0*y1+z0*z1;
if(cosOmega<0.0f){
w1=-w1;
x1=-x1;
y1=-y1;
z1=-z1;
cosOmega=-cosOmega;
}
float k0,k1;
if(cosOmega>0.9999f)
{
k0=1.0f-t;
k1=t;
}else{
float sinOmega=sqrt(1.0f-cosOmega*cosOmega);
float omega=atan2(sinOmega,cosOmega);
flat oneOverSinOmega=1.0f/sinOmega;
k0=sin((1.0f-t)*omega)*oneOverSinOmega;
k1=sin(t*omega)*sinOverSinOmega;
}
w=w0*k0+w1*k1;
x=x0*k0+x1*k1;
y=y0*k0+wy1*k1;
z=z0*k0+z1*k1;
上述的代码仅仅以单位四元数为基础坐标系描述旋转的插值,根据书本前部分的讨论,从 q 0 q_{0} q0到 q 1 q_{1} q1四元数之差 Δ q = q 1 q 0 − 1 \Delta q=q_{1}q_{0}^{-1} Δq=q1q0−1,取这段差的一小部分t可表示为 ( Δ q ) t (\Delta q)^{t} (Δq)t,以 q 0 q_{0} q0点为坐标系变换到原坐标系则表示为 ( Δ q ) t q 0 (\Delta q)^{t}q_{0} (Δq)tq0,这样可以描述任意四元数到其它四元数旋转插值的过程。
四元数中有一个专门的函数表示这种变换:
s
l
e
r
p
(
q
0
,
q
1
,
t
)
=
(
q
1
q
0
−
1
)
t
q
0
slerp(q_{0},q_{1},t)=(q_{1}q_{0}^{-1})^{t}q_{0}
slerp(q0,q1,t)=(q1q0−1)tq0
这种代数的表示往往需要消耗更多的计算资源.实际上采用的是一种数学上相等的计算形式。我们将采用二维平面扩展到四维超平面的过程来描述这种变换,如图所示
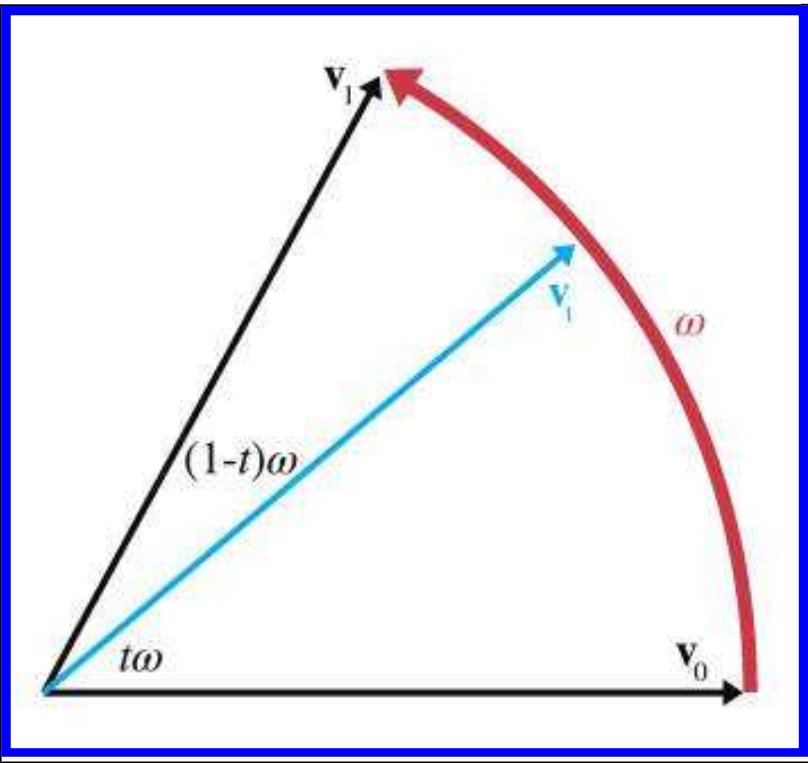
从平面上的点
v
0
v_{0}
v0到
v
1
v_{1}
v1需要旋转
ω
\omega
ω度,我们要找到一种普适的计算来表达
s
l
e
r
p
(
v
0
,
v
1
,
t
)
slerp(v_{0},v_{1},t)
slerp(v0,v1,t),继而扩展到
s
l
e
r
p
(
q
0
,
q
1
,
t
)
slerp(q_{0},q_{1},t)
slerp(q0,q1,t)
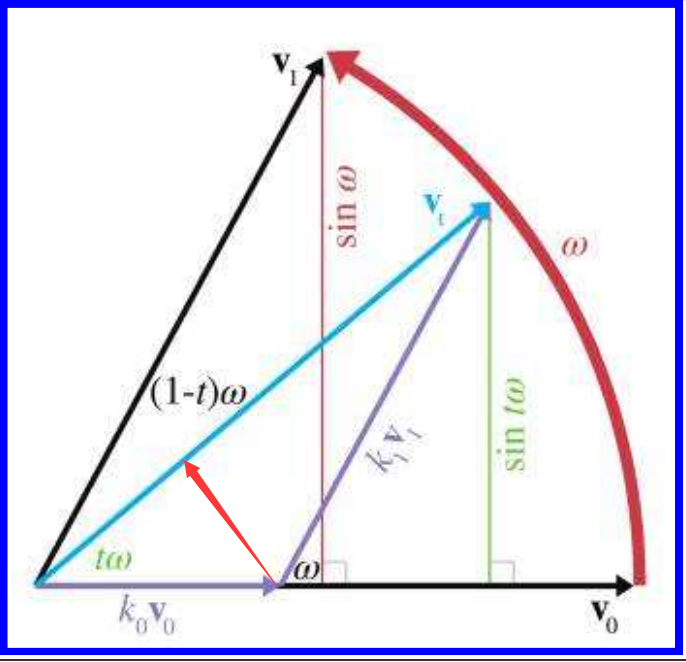
对于以
k
1
v
1
k_{1}v_{1}
k1v1为斜边的三角形可以得出
s
i
n
(
ω
)
=
s
i
n
(
t
ω
)
k
1
k
1
=
s
i
n
(
t
ω
)
s
i
n
ω
sin(\omega)=\frac{sin(t\omega)}{k_{1}}\\ k_{1}=\frac{sin(t\omega)}{sin\omega}
sin(ω)=k1sin(tω)k1=sinωsin(tω)
以红色箭头作为由
k
0
v
0
k_{0}v_{0}
k0v0和
k
1
v
1
k_{1}v_{1}
k1v1组成的三角形的中垂线,由
v
1
v_{1}
v1和
k
1
v
1
k_{1}v_{1}
k1v1平行可知
k
0
∥
v
0
∥
s
i
n
(
t
ω
)
=
k
1
∥
v
1
∥
s
i
n
(
1
−
t
)
ω
k_{0}\left \| v_{0}\right \|sin(t\omega)=k_{1}\left \| v_{1}\right \|sin(1-t)\omega
k0∥v0∥sin(tω)=k1∥v1∥sin(1−t)ω
四元数旋转后模不变可得
∥
v
0
∥
=
∥
v
1
∥
\left \|v_{0}\right \|=\left \| v_{1}\right \|
∥v0∥=∥v1∥,那么:
k
0
s
i
n
(
t
ω
)
=
k
1
s
i
n
(
1
−
t
)
ω
k
0
=
k
1
s
i
n
(
1
−
w
)
s
i
n
(
w
)
k_{0}sin(t\omega)=k_{1}sin(1-t)\omega\\ k_{0}=\frac{k_{1}sin(1-w)}{sin(w)}
k0sin(tω)=k1sin(1−t)ωk0=sin(w)k1sin(1−w)
由于
k
1
=
s
i
n
(
t
ω
)
s
i
n
ω
k_{1}=\frac{sin(t\omega)}{sin\omega}
k1=sinωsin(tω),化简可得
k
0
=
s
i
n
(
1
−
w
)
s
i
n
(
w
)
k_{0}=\frac{sin(1-w)}{sin(w)}
k0=sin(w)sin(1−w)
既然如此,
v
t
v_{t}
vt可以被表示为
v
t
=
k
0
v
0
+
k
1
v
1
=
s
i
n
(
1
−
t
)
w
s
i
n
w
v
0
+
s
i
n
(
t
w
)
s
i
n
(
w
)
v
1
v_{t}=k_{0}v_{0}+k_{1}v_{1}=\frac{sin(1-t)w}{sinw}v_{0}+\frac{sin(tw)}{sin(w)}v_{1}
vt=k0v0+k1v1=sinwsin(1−t)wv0+sin(w)sin(tw)v1
相同的基本思想可以扩展到四元数空间,我们可以将slerp改写为
s
l
e
r
p
(
q
0
,
q
1
,
t
)
=
s
i
n
(
1
−
t
)
w
s
i
n
w
q
0
+
s
i
n
(
t
w
)
s
i
n
(
w
)
q
1
slerp(q_{0},q_{1},t)=\frac{sin(1-t)w}{sinw}q_{0}+\frac{sin(tw)}{sin(w)}q_{1}
slerp(q0,q1,t)=sinwsin(1−t)wq0+sin(w)sin(tw)q1
C++代码如下
float w0,x0,y0,z0;
float w1,x1,y1,z1;
float t;
float w,x,y,z;
float cosOmega=w0*w1+x0*x1+y0*y1+z0*z1;
if(cosOmega<0.0f){
w1=-w1;
x1=-x1;
y1=-y1;
z1=-z1;
}
float k0,k1;
if(cosOmega>0.9999f)
{
k0=1.0f-t;
k1=t;
}else{
float sinOmega=sqrt(1.0f-cosOmega*cosOmega);
float omega=atan2(sinOmega,cosOmega);
float oneOverSinOmega=1.0f/sinOmega;
k0=sin((1.0f-t)*omega)*oneOverSinOmega;
k1=sin(t*omega)*oneOverSinOmega;
}
//interpolation
w=w0*k0+w1*k1;
x=x0*k0+w1*k1;
y=y0*k0+y1*k1;
z=z0*k0+z1*k1;
Reference:<<3D Math Primer for Graphics and Game Development>> P246~P263






















 1541
1541











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








