相容/不相容非齐次线性方程组的最小二乘解与最佳最小二乘解

首先说明相容/不相容非齐次线性方程组的概念：

（1）线性方程组Ax=b有解的充要条件是rank(A,b)=rank(A)，此时称Ax=b是相容非齐次线性方程组；

（2）对Ax=b，若rank(A,b)≠rank(A)，即b∉R(A)时，方程组Ax=b无解，此时称Ax=b是不相容非齐次线性方程组。

下面正式开始。

---

问题：假设x₁,x₂,…,x_n和y满足线性关系，其中x₁,x₂,…,x_n是n个自变量，y是因变量，有y=a₁x₁+…+a_nx_n，现在总共有s组观测值如下：

求a₁,a₂,…,a_n？

求解过程如下：

首先，可构建方程组如下：

上图是一个线性方程组，如果能求出解自然万事OK，但是极有可能是无解的。

在无解的情况下只能求近似解，要求近似解的误差最小，可以构建函数：

求图中函数的最小值即可。

常规做法是这样的：分别求偏导数并令其为0，即∂f/∂a_i=0，其中i=1,2,…,n。最后便可以得到α₁,α₂,…,α_n。

下面使用内积空间的投影理论解决不相容方程组Ax=b的解。

令s×n阶矩阵A为：

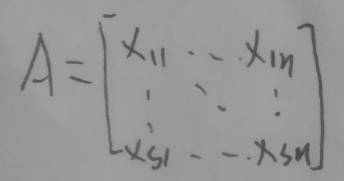
令A=[α₁,α₂,…,α_n]，其中α_i是A的第i个列向量，其中i=1,2,…,n，令向量b=[y₁,y₂,…,y_s]^T，x=[a₁,a₂,…,a_n]^T，则有：Ax=b，即：

令W=span{α₁,α₂,…,α_n}，α_i∈R^s，其中i=1,2,…,n。则W是s维向量空间的一个线性子空间，b∈R^s。若向量b在子空间W内，则方程组有解，否则无解，即为如下情况：

设向量y=Ax，现在问题转换为求x使向量Ax与向量b之间的距离d(b,Ax)最小，易知在子空间W上的所有向量中，b在W上的投影与b之间的距离最小，于是，当y=Ax为b在W上的投影时的那个x，就是Ax=b的近似解。

由于y现在是b在W上的投影，因此有b-y⊥W，即b-y⊥span{α₁,α₂,…,α_n}，于是有b-y⊥α_i，其中i=1,2,…,n。

根据内积运算有：<α_i,b-Ax>=0，于是<α_i,b>=<α_i,Ax>=<α_i,a₁α₁+…+a_nα_n>，因此<α_i,b>=a₁<α_i,α₁>+…+a_n<α_i,α_n>，其中i=1,2,…,n。写成矩阵方程为：

即G(α₁,α₂,…,α_n)·x=G(α₁,α₂,…,α_n;b)，其中G(α₁,α₂,…,α_n)为α₁,α₂,…,α_n的Gram矩阵，G(α₁,α₂,…,α_n;b)为α₁,α₂,…,α_n和b的协Gram矩阵。

需要注意的是G(α₁,α₂,…,α_n)不一定可逆，因为A的列向量组α₁,α₂,…,α_n不一定是线性无关向量组，当是线性无关向量组时，直接令x=G(α₁,α₂,…,α_n)^-1·G(α₁,α₂,…,α_n;b)即可得到解x=[a₁,a₂,…,a_n]^T。但是无论是否为线性无关向量组，都有以下结论。

首先对于方程组G(α₁,α₂,…,α_n)·x=G(α₁,α₂,…,α_n;b)，即A^HAx=A^Hb，这依然是一个非齐次的线性方程组，下面讨论该方程组的系数矩阵即A^HA的秩与增广矩阵[A^HA,A^Hb]的秩之间的关系。

首先有rank(A^HA)≤rank(A^HA,A^Hb)，毕竟增加列数可能使矩阵秩增加，对吧。

而rank(A^HA,A^Hb)=rank[A^H(A,b)]≤rank(A^H)，毕竟两个矩阵乘积的秩小于等于任意其中一个矩阵的秩，对吧。

在实数域上有rank(A)=rank(A^H)=rank(A^T)。

下面的内容全部建立在实数域上，但是使用A^H表示A^T。

将方程组Ax=0的解x代入A^HAx=0一定成立，即Ax=0的解一定是A^HAx=0的解。若x是方程组A^HAx=0的解，对A^HAx=0左右两边同左乘向量x的共轭转置x^H得到x^HA^HAx=0，则<Ax,Ax>=0，则有Ax=0，即A^HAx=0的解一定是Ax=0的解。综上所述A^HAx=0与Ax=0是同解方程组，则二者的系数矩阵的秩相同，即rank(A^HA)=rank(A)。

而rank(A)=rank(A^H)，则rank(A^HA)=rank(A)=rank(A^H)。又因为rank(A^HA,A^Hb)=rank[A^H(A,b)]≤rank(A^H)=rank(A)=rank(A^HA)，即rank(A^HA,A^Hb)≤rank(A^HA)，且有rank(A^HA)≤rank(A^HA,A^Hb)，最后有rank(A^HA)=rank(A^HA,A^Hb)。

即对于方程组A^HAx=A^Hb来说，系数矩阵即A^HA的秩与增广矩阵[A^HA,A^Hb]的秩相等，因此方程组A^HAx=A^Hb总有解，即方程组G(α₁,α₂,…,α_n)·x=G(α₁,α₂,…,α_n;b)总有解，这个方程组的任意一个解α都是方程组Ax=b的近似解，这样便解决了博文开头的问题。

如果能求得比较好的解就更好了，那什么样的解是比较好的呢？

（1）对于相容的方程，称相容方程组Ax=b的所有解x中模(2-范数)最小的解是Ax=b的最小模解，其中x的2-范数是||x||=sqrt(x^Hx)。

（2）对于不相容的方程，也希望有方程的“解”，并要求所得到的“解”是方程组的最小二乘解与最佳最小二乘解。下面对最小二乘解与最佳最小二乘解进行解释。

设A∈C^m×n，b∈C^m，n维列向量x₀满足对于任何一个n维列向量x，都有||Ax₀-b||² ≤||Ax-b||²，则称x₀是方程组Ax=b的一个最小二乘解。若μ是最小二乘解，如果对于任一个最小二乘解x₀，都有不等式||μ||≤||x₀||，则称μ是最佳最小二乘解或者最小范数最小二乘解。

定理：设A∈C^m×n，B∈C^n×m，则下列两个命题是等价的：

(1) 对于任给b∈C^m，则x=Bb一定是Ax=b的最小二乘解；

(2) (AB)^H=AB，ABA=A。

上述定理说明方程组Ax=b的最小二乘解是x=Bb，其中B是A的广义逆矩阵A^-，且B需满足(AB)^H=AB。

最后需要指出，x=A⁺b是方程组Ax=b的最佳最小二乘解，其中A⁺是矩阵A的加号逆。

---

总结：

（1）对于相容非齐次线性方程组Ax=b，最好的解是最小模解。

（2）对不相容非齐次线性方程组Ax=b，最好的解是最佳最小二乘解x=A⁺b。