1 置信区间 confidence interval
population parameter的预测区间
换句话说θ有1-α的概率落在这个置信区间内
1.1 :已知方差的正态分布的均值 的置信区间
举个例子:已知方差的正态分布的均值,的置信区间
随着置信等级的提升,置信区间的范围也在不断增加
1.2 从误差的角度理解置信区间
如果均值
是μ的预测,那么一个人有(1-α)的信心μ和
的误差不会超过
该值被称为误差边界(margin of error)
再换种方式理解:如果均值是μ的预测,那么一个人有(1-α)的信心μ和
的误差不会超过e,当样本的大小≥

1.3 单边置信区间

1.4 未知方差的正态分布的均值 的置信区间


1.5 未知分布,未知均值,未知方差(但是样本数量很多)的均值置信区间

1.6 两个分布均值之差的置信区间
- population distribution为正态分布,已知标准差σ1和σ2
- population distribution非正态分布,已知标准差σ1和σ2,样本数量多(大于30)
- population distribution 非正态分布,未知标准差,样本数量多(大于30)
- population distribution是正态分布,未知方差,样本不多(小于30)
- 两个未知方差相等(是否相等可以通过F-test判断)
推导:
——>
t 分布的定义
于是有
为自由度是n1+n2-2的t分布
- population distribution是正态分布,未知方差,样本不多(小于30)
- 两个未知方差不等
其中自由度为:
1.7 配对样本(paired sample)之间均值的置信区间
(比如不同时刻对应数据之差)

1.7.0 何为配对样本
这就需要和上一小节(1.6)做对比了,上一小节中,两组样本是独立采样的,互不影响,而对于配对样本,每一组样本之间是互相影响的(比如同一位置浅海和深海的气压,那么两个样本之间是一一确定的)
因此paired sample 又被称为dependent sample
1.7.1 两个population distribution 为正态分布,未知方差,样本不大
由于我们比较的只是paired sample的均值查,所以我们使用的是单样本的t分布
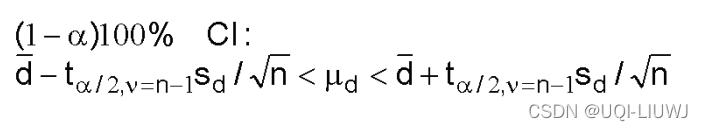
1.8 大量样本的概率 的置信区间
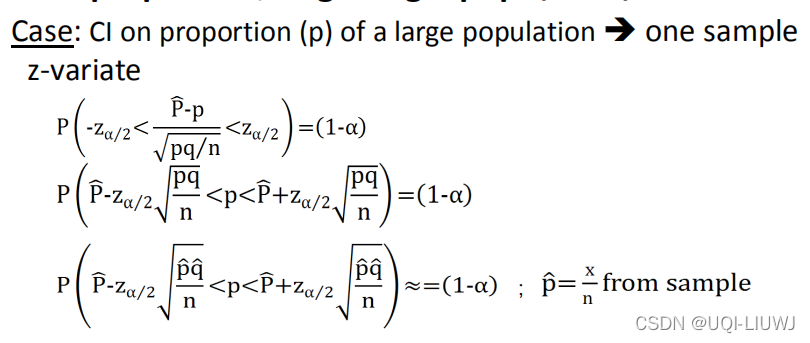
1.8.1 误差边界
如果我们把刚才得到的
作为概率p的点估计,那么我们有(1-α)100%的信心误差不会超过
这个值也被称之为误差边界
如果我们把刚才得到的
作为概率p的点估计,那么我们有(1-α)100%的信心误差不会超过e,只要样本的数量大于
我们不难发现,当
的时候,
是最大的,
只要n大于这个值,那么他就有(1-α)100%的信心误差不超过e,不管p实际值是多少
1.9 两个独立样本概率之差的置信区间
如果两个样本的数量很多的话

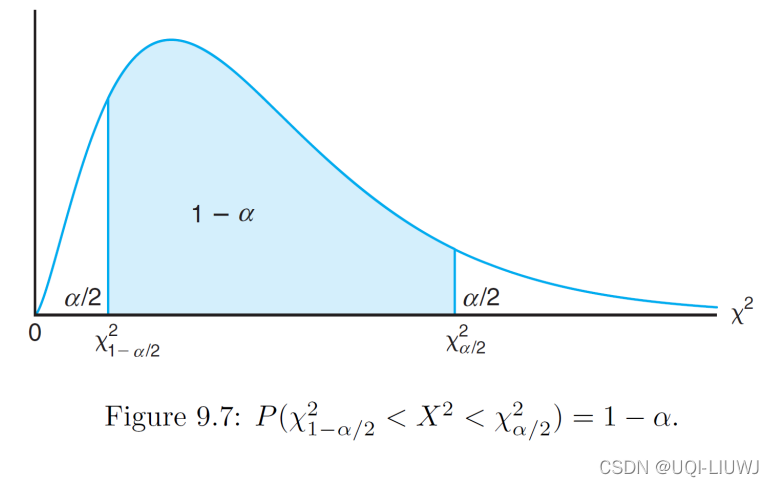
1.10 population distribution为正态分布,方差的置信区间
对样本大小没有限制
注意chi-square 看的是右侧围的面积
1.11 population distribution为正态分布,两个样本方差的比例

倒数第二步使用了f分布的性质
注意F分布也是看右边围的区域的
2 预测区间 prediction interval
预测区间的价值在于它们表达了预测中的不确定性。 如果我们只生成点预测,则无法判断预测的准确程度。 但是,如果我们还生成预测区间,那么很明显每个预测与多少不确定性相关联
2.1 已知方差未知均值的正态分布
根据population,预测一个新样本的估计区间
假设我们有n个样本,他们的population distribution是未知均值μ,已知方差σ^2的正态分布,这一组样本均值的点估计为
假设又来了一个服从相同分布的观测值
,那么
2.2 未知方差的正态分布
由于这时候还是满足正态分布的,所以即使样本数量大也没关系
可以看到,PI比CI会更宽一点
3 容忍区间 tolerance interval
population 中特定比例的观测样本的区间
容忍区间是用样本数据来估算表示指定比例的总体上下限(而不是平均值)的不确定程度的。
以正态分布为例:95%的样本是位于μ±1.96σ中的
3.1 tolerance limit
未知均值,未知方差的正态分布,观测值的比例
——>我们需要确定k,使得我们有(1-γ)*100%的信心,至少(1-α)的数据囊括在区间 中
3.1.1 tolarance limit的的分布表
(巧计法:先有信心,再有数据)

3.1.2 举例

注意这里容忍区间查表的时候,n不用减一








 本文详细介绍了统计学中的置信区间、预测区间和容忍区间的概念及其计算方法。置信区间用于估计总体参数,如均值和方差,随着置信水平提高,区间范围扩大;预测区间关注预测值的不确定性,而容忍区间则关注包含总体特定比例数据的范围。文中通过实例和公式展示了各种情况下的区间计算,包括正态分布和非正态分布的情况,以及大样本和小样本的处理。此外,还讨论了配对样本和大量样本的处理方法,为数据分析提供了深入的理解。
本文详细介绍了统计学中的置信区间、预测区间和容忍区间的概念及其计算方法。置信区间用于估计总体参数,如均值和方差,随着置信水平提高,区间范围扩大;预测区间关注预测值的不确定性,而容忍区间则关注包含总体特定比例数据的范围。文中通过实例和公式展示了各种情况下的区间计算,包括正态分布和非正态分布的情况,以及大样本和小样本的处理。此外,还讨论了配对样本和大量样本的处理方法,为数据分析提供了深入的理解。


















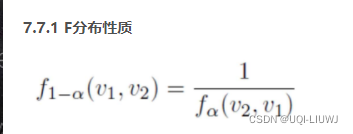






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










