logistic回归概率详解

logistic回归概率详解

上一篇我们介绍了线性代数的基本知识，并以PCA作为案例进行了讲解。在本篇中，我们依然按照相同的思路进行开展：首先复习一下概率的相关知识，最后以对率回归（对数几率回归）为案例进行讲解。

1. 概率论

AI圣经《deep learning》一书把线性代数、概率与信息论和数值计算三部分作为机器学习中基础的数学知识进行单独设置章节来讲解，可见这几部分对机器学习乃至深度学习的重要性。 
所以我们本篇复习一下高中到大学学习过的概率论知识（至于信息论的知识，我们会到基础机器学习的版块和相关案例结合一起讲解），希望和大家一起学习进步。

1.1定义

在这里，我们采取和统计二者的对比来介绍概率论的相关定义。

• 统计推断是根据观测的数据，反向思考其数据生成过程，即黑箱子的内部结构做出分析，并提出各种假设，这些假设都是概率模型
• 概率论是统计推断的基础，许多定理与结论，如大数定理、中心极限定理等保证了统计推断的合理性。
• 预测、分类、聚类、估计等，都是统计推断的特殊形式，强调对于数据生成过程的研究。

简而言之，统计是演绎分析，概率为归纳总结。形象而言，统计是黑箱子 ，我们通过手里的黑白球来推断箱子里的球的分布；概率则是透明箱子 ，我们通过箱子里的球的状况总结分布，从而判断手中球的颜色概率。

1.2随机变量

首先，具有以下三个特征的试验称为随机试验（用E来表示）：

1. 试验可以在相同的条件下重复进行；
2. 试验可能出现的结果是事先预知的；
3. 每次试验有且只有其中一个结果出现，但在每次试验结束之前，不知道哪一个结果会出现。

在随机试验中，实验的结果中每一个可能发生的事件叫做实验的样本点（Sample point，通常用x来表示）；所有的样本点x1，x2，x3···，xn构成的集合叫做样本空间（Sample space，通常用S来表示）： 

S={x1，x2，x3···，xn}

介绍了以上知识点后，我们假设随机试验E的样本空间为S，如果对每一个样本点e∈S，都有唯一的实数值X(e)与之对应，则称x(e)为S上的随机变量 ，简记为X。 
引入随机变量 后，我们就可以用随机变量来描述随机事件，例如在一次投篮试验中，可用“X=1”表示事件“投中”，用“X=0”表示事件“未投中”；又如，用X表示一次共10名运动员投篮试验中投中的次数，则“X>5”表示事件“投中超过5球”。

 

1.3概率分布

随机变量根据能否一一列举（不是有限与无限）分为离散型和非离散型，其中非离散型主要指连续型随机变量。我们将根据这两类来介绍其概率分布：

离散型

1.伯努利分布（Bernoulli分布，0-1分布） 

2.多次试验伯努利，二项分布：X~B(n,p)

 

 

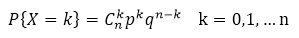
3.由泊松定理：

 

 

 

二项分布的极限分布是泊松分布：X~P(λ) 
当n很大（n≥10），p很小（p＜0.1）时，有

 

 

 

4.Multinoulli分布 
多项分布特例，伯努利分布的高维形式（向量形式）：

 

 

 

 

连续型

1.均匀分布：X~U(a,b) 

 

2.指数分布：X~E(λ)

 

 

 

3.与指数分布相联系的： Laplace 分布

 

 

 

3.正态分布：X~N(μ，σ^2)

 

 

 

正态分布三大特性：

 

• f(x)关于x=μ对称
• f(x)关于x=μ时取最大值
• 曲线y=f(x)在x=μ±σ处有拐点，当x→﹢∞，曲线以x轴为渐近线

关于正态分布，还有多维和混合的形式。

4.狄拉克分布（Dirac分布） 

 

与狄拉克分布相关的经验分布

 

 

 

 

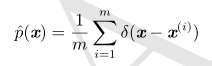
2. logistic回归

2.1由来

正统说来，应该首先说说线性回归，即y=wTx+b的模型。但这部分知识较为简单，读者可以自行查阅西瓜书或者其他资料，在这里我们不再赘述。

如果我们希望输入输出之间由线性到非线性之间的映射转换，我们可以采取很多办法：

例如将 

y=wTx+b 

转化为 

ln y=wTx+b 

就得到了从线性回归到对数（log）线性回归的转换过程。

 

继续深挖，信号专业应该有一个激活函数叫单位阶跃函数，如下图所示： 

 

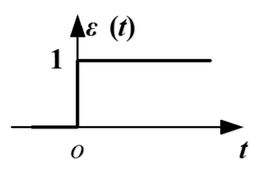
其不够顺滑，用sigmoid函数来代替：

 

 

 

 

 

sigmoid函数拥有良好性质：值域（0,1）；单调可微；x=0附近变化很陡

 

那么，我们如果把线性回归的输出y值（也就是sigmoid的输入量z）映射为相应的概率（0~1之间），从而就与概率论知识（主要是二分类任务，所以针对于伯努利分布）结合起来。

具体而言，我们有以下公式： 

 

继续变换为类似对数线性回归的形式：

 

 

 

所以，logistic regression翻译为“对数几率回归”而非“逻辑回归”源自于上述公式：y/(1-y)称为几率（odds），反映x作为正例的可能性；如果将y/(1-y)看成一个整体，则上式就是对数线性回归。

 

且这里虽名为“回归”，实际是一种“分类”，具体是一种“0-1分类”。（由西瓜书1.2基本术语一节知，预测值为离散值此类任务为“分类”；反之为“回归”）

2.2深入分析

有了上述基本知识作为铺垫，我们继续深入探究对率回归。

首先，我们把y看成正样本（1-y为负样本）的概率（类后验概率）： 

 

在一次试验中，我们发现上述满足伯努利分布，则有：

 

 

 

其中，

 

 

 

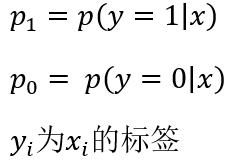
我们采用对数化使其便于求解： 
（1） 

 

 

换一个角度思考，从机器学习的思想出发，我们的策略应该是首先设立一个代价函数，然后对其进行优化。

常见的代价函数有： 
1. 0-1代价函数（0-1 cost function） 

 

2. 平方代价函数（quadratic cost function)

 

 

3. 绝对值代价函数(absolute cost function) 

 

4. 对数代价函数（logarithmic cost function) 或对数似然代价函数(log-likehood cost function)

 

 

 

 

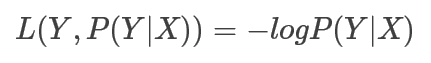
我们采用对数损失函数作为logistic rg的cost function，则有：

 

 

转化一下，变为： 
（2） 

 

当yi=1时，即这个样本为正类。

 

如果此时y ̂=1,则对这个样本而言的cost=0,表示这个样本的预测完全准确。

如果此时预测的概率y ̂=0，那么cost→∞。直观解释的话，由于此时样本为一个正样本，但是预测的结果p(y=1|x)=0, 也就是说预测 y=1的概率为0，那么此时就要对损失函数加一个很大的惩罚项。

一般说来y ̂的值为0~1之间的一个实数，表明的是样本为正或者为负的概率，这个概率值的大小影响着cost的大小。我们也是通过这个影响来调整我们所需的参数权重w和偏置b。

当y=0时，推理过程跟上述完全一致，不再累赘。

对比（1）（2），我们发现两者解释最后得出的结论一致。

当然，（1）（2）仅仅是一次试验（样本）的内容，我们针对全体样本，不管是从概率角度出发，还是总体的代价函数，都为： 

 

 

至于求解包括我们还未提到的贝叶斯公式，我们将在以后学习中讲解。下一篇我们针对数值优化问题并以SVM为例，做个巩固。