线段和四边形的交点计算

线段和四边形的交点计算，可以转化为线段和四边形的四条边各自进行交点计算，而线段和线段交点计算的原理已经在之前的一篇博客中介绍过了，这里不再赘述。
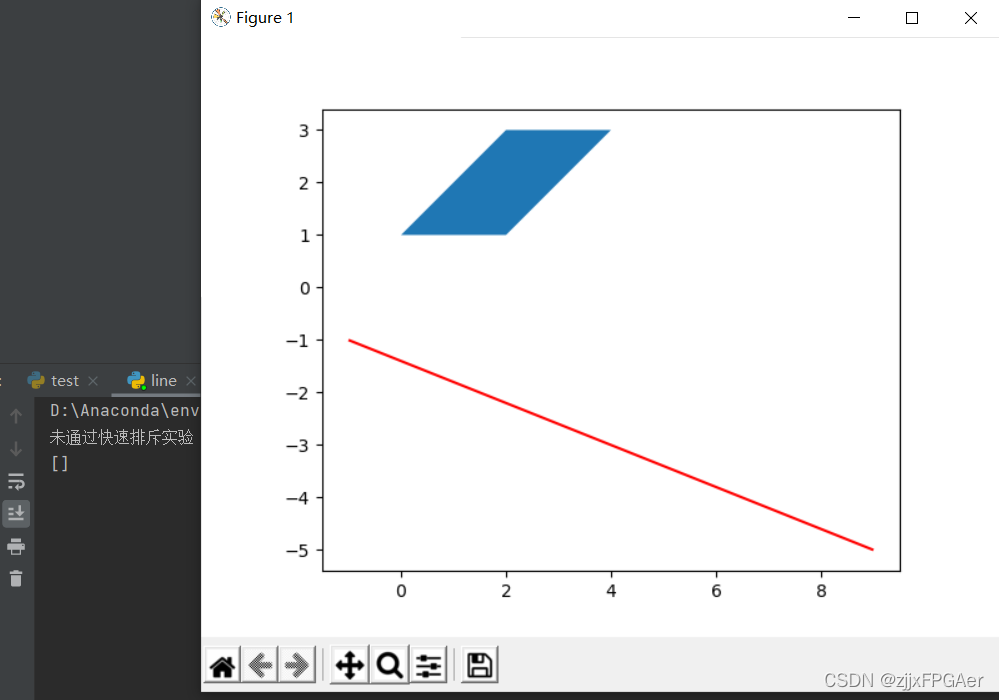
为了加快速度，在计算和四条边的交点之前，我们先进行一个快速排斥实验，即判断线段的最小包围盒是否和四边形的最小包围盒相交，若不相交，则无需再进行交点的计算，可节省下相等一部分的计算量。
以下是python代码实现:

import geopandas
from shapely import geometry
import operator
import matplotlib.pyplot as plt

def findIntersection(x1, y1, x2, y2, x3, y3, x4, y4):        #求直线交点
    t=((x1-x2)*(y3-y4)-(y1-y2)*(x3-x4))
    if t!=0:                 #有交点
        px = ((x1 * y2 - y1 * x2) * (x3 - x4) - (x1 - x2) * (x3 * y4 - y3 * x4)) / t
        py = ((x1 * y2 - y1 * x2) * (y3 - y4) - (y1 - y2) * (x3 * y4 - y3 * x4)) / t
        return [px,py]
    else:
        return None

def findLineIntersection(p1,p2,p3,p4):         #求线段p1p2和线段p3p3的交点
    x1,y1=p1
    x2,y2=p2
    x3,y3=p3
    x4,y4=p4
    #
    t = ((x1 - x2) * (y3 - y4) - (y1 - y2) * (x3 - x4))
    if t != 0:  # 有交点
        px = ((x1 * y2 - y1 * x2) * (x3 - x4) - (x1 - x2) * (x3 * y4 - y3 * x4)) / t
        py = ((x1 * y2 - y1 * x2) * (y3 - y4) - (y1 - y2) * (x3 * y4 - y3 * x4)) / t
        if px>=min(x1,x2) and px<=max(x1,x2) and px>=min(x3,x4) and px<=max(x3,x4):      #交点在线段上
            return [px, py]
        else:
            return None
    else:
        return None

def isIntersect(line,parallelogram):
    l1,l2=line
    p1,p2,p3,p4=parallelogram
    x1,x2=min(l1[0],l2[0]),max(l1[0],l2[0])
    y1,y2=min(l1[1],l2[1]),max(l1[1],l2[1])                           #线段的最小包围盒
    x3,x4=min(p1[0],p2[0],p3[0],p4[0]),max(p1[0],p2[0],p3[0],p4[0])
    y3,y4=min(p1[1],p2[1],p3[1],p4[1]),max(p1[1],p2[1],p3[1],p4[1])   #四边形的最小包围盒
    #
    if x1<=x4 and x3<=x2 and y1<=y4 and y3<=y2:
        return True
    else:
        return False


def findParallelogramIntersection(line,parallelogram):          #求线段和平行四边形的交点
    if not isIntersect(line,parallelogram):
        #未通过快速排斥实验,一定不相交
        print("未通过快速排斥实验")
        return []
    l1,l2=line
    p1,p2,p3,p4=parallelogram
    cp1=findLineIntersection(l1,l2,p1,p2)
    cp2=findLineIntersection(l1,l2,p2,p3)
    cp3=findLineIntersection(l1,l2,p3,p4)
    cp4=findLineIntersection(l1,l2,p4,p1)
    old_cps=[]
    if cp1:
        old_cps.append(cp1)
    if cp2:
        old_cps.append(cp2)
    if cp3:
        old_cps.append(cp3)
    if cp4:
        old_cps.append(cp4)
    #print(old_cps)
    cps=[]
    for cp in old_cps:
        if cp not in cps:
            cps.append(cp)
    #print(cps)
    return cps

if __name__=="__main__":
    line=[(-1,-1),(9,-5)]
    parallelogram=[(0,1),(2,1),(4,3),(2,3)]
    ax=geopandas.GeoSeries(geometry.LineString(line)).plot(color='r')
    geopandas.GeoSeries(geometry.Polygon(parallelogram)).plot(ax=ax)
    points=findParallelogramIntersection(line,parallelogram)
    print(points)
    assert len(points)<=2
    if len(points)==2:
        geopandas.GeoSeries([geometry.Point(points[0]),geometry.Point(points[1])]).plot(ax=ax,color='r')
    plt.show()

结果

1.未通过快速排斥实验的情况

2.通过快速排斥实验但没交点

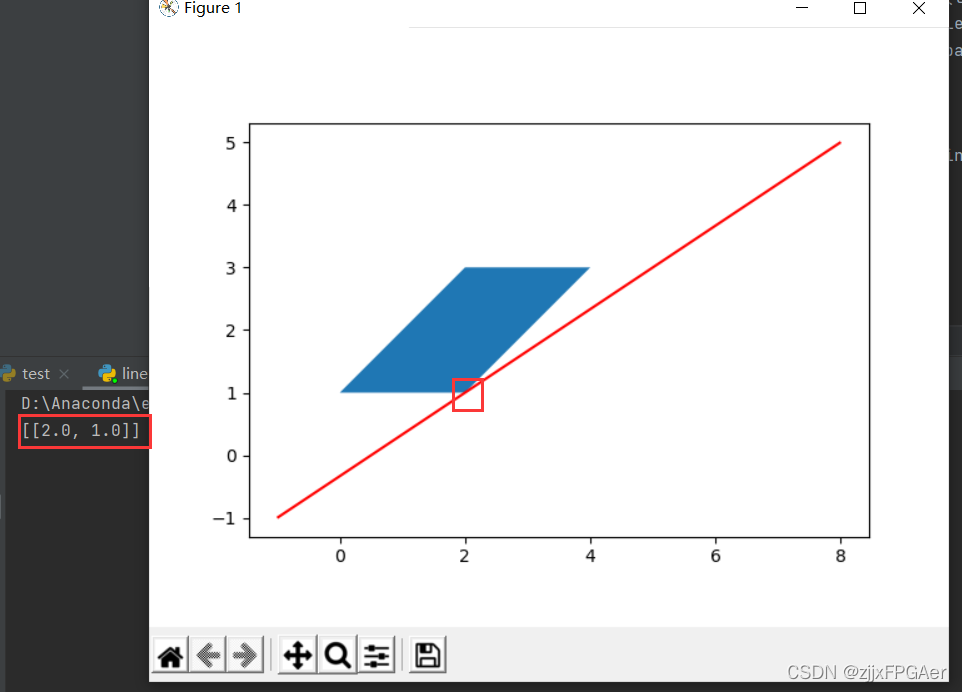
3.有一个交点

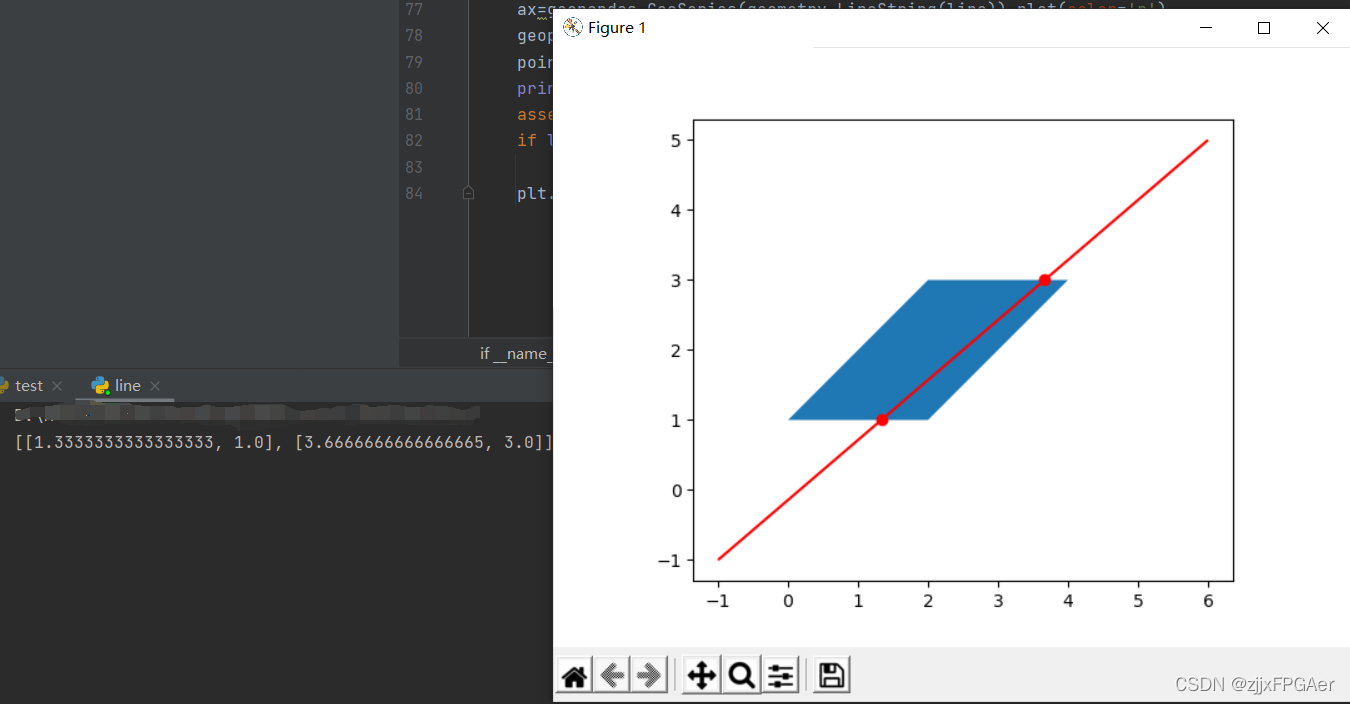
4.两个交点

改进

之前的代码，由于计算机在表示数据时存在误差，因此有时会发生错误(当四边形的某条边垂直或平行于X轴时)，现加入了一个误差容忍因子eps,解决了这个问题。代码如下

import geopandas
from shapely import geometry
import operator
import matplotlib.pyplot as plt

def findIntersection(x1, y1, x2, y2, x3, y3, x4, y4):        #求直线交点
    t=((x1-x2)*(y3-y4)-(y1-y2)*(x3-x4))
    if t!=0:                 #有交点
        px = ((x1 * y2 - y1 * x2) * (x3 - x4) - (x1 - x2) * (x3 * y4 - y3 * x4)) / t
        py = ((x1 * y2 - y1 * x2) * (y3 - y4) - (y1 - y2) * (x3 * y4 - y3 * x4)) / t
        return [px,py]
    else:
        return None

def findLineIntersection(p1,p2,p3,p4):         #求线段p1p2和线段p3p3的交点
    eps=1e-6
    x1,y1=p1
    x2,y2=p2
    x3,y3=p3
    x4,y4=p4
    #
    t = ((x1 - x2) * (y3 - y4) - (y1 - y2) * (x3 - x4))
    if t != 0:  # 有交点
        px = ((x1 * y2 - y1 * x2) * (x3 - x4) - (x1 - x2) * (x3 * y4 - y3 * x4)) / t
        py = ((x1 * y2 - y1 * x2) * (y3 - y4) - (y1 - y2) * (x3 * y4 - y3 * x4)) / t
        if px>=min(x1,x2)-eps and px<=max(x1,x2)+eps and px>=min(x3,x4)-eps and px<=max(x3,x4)+eps and \
           py>=min(y1,y2)-eps and py<=max(y1,y2)+eps and py>=min(y3,y4)-eps and py<=max(y3,y4)+eps:      #交点在线段上
            return [px, py]
        else:
            return None
    else:
        return None

def isIntersect(line,parallelogram):
    l1,l2=line
    p1,p2,p3,p4=parallelogram
    x1,x2=min(l1[0],l2[0]),max(l1[0],l2[0])
    y1,y2=min(l1[1],l2[1]),max(l1[1],l2[1])                           #线段的最小包围盒
    x3,x4=min(p1[0],p2[0],p3[0],p4[0]),max(p1[0],p2[0],p3[0],p4[0])
    y3,y4=min(p1[1],p2[1],p3[1],p4[1]),max(p1[1],p2[1],p3[1],p4[1])   #四边形的最小包围盒
    #
    if x1<=x4 and x3<=x2 and y1<=y4 and y3<=y2:
        return True
    else:
        return False


def findParallelogramIntersection(line,parallelogram):          #求线段和平行四边形的交点
    if not isIntersect(line,parallelogram):
        #未通过快速排斥实验,一定不相交
        #print("未通过快速排斥实验")
        return []
    l1,l2=line
    p1,p2,p3,p4=parallelogram
    cp1=findLineIntersection(l1,l2,p1,p2)
    cp2=findLineIntersection(l1,l2,p2,p3)
    cp3=findLineIntersection(l1,l2,p3,p4)
    cp4=findLineIntersection(l1,l2,p4,p1)
    old_cps=[]
    if cp1:
        old_cps.append(cp1)
    if cp2:
        old_cps.append(cp2)
    if cp3:
        old_cps.append(cp3)
    if cp4:
        old_cps.append(cp4)
    #print(old_cps)
    cps=[]
    for cp in old_cps:
        if cp not in cps:
            cps.append(cp)
    #print(cps)
    return cps

if __name__=="__main__":
    line=[(-1,-1),(6,5)]
    parallelogram=[(0,1),(2,1),(4,3),(2,3)]
    ax=geopandas.GeoSeries(geometry.LineString(line)).plot(color='r')
    geopandas.GeoSeries(geometry.Polygon(parallelogram)).plot(ax=ax)
    points=findParallelogramIntersection(line,parallelogram)
    print(points)
    assert len(points)<=2
    if len(points)==2:
        geopandas.GeoSeries([geometry.Point(points[0]),geometry.Point(points[1])]).plot(ax=ax,color='r')
    plt.show()