机器人运动学学习-齐次变化矩阵的推导-单个关节运动的平移矩阵和旋转矩阵证明

驽马匠人

已于 2024-03-19 13:58:30 修改

阅读量1k

点赞数 6

分类专栏：刚体运动学/动力学文章标签：机器人学习矩阵算法线性代数

于 2024-03-19 13:57:15 首次发布

本文链接：https://blog.csdn.net/qq_40326539/article/details/136833036

版权

刚体运动学/动力学专栏收录该内容

4 篇文章 0 订阅

订阅专栏

机器人学中我们是通过齐次矩阵来描述机器人的关节运动，接下来我们详细的证明下齐次矩阵的推导过程

1.齐次变化矩阵的标准写法

$T=\begin{bmatrix} R & P\\ 0&1 \end{bmatrix}= \begin{bmatrix} n_{x} & o_{x} & a_{x} & p_{x} \\ n_{y} & o_{y} & a_{y} & p_{y} \\ n_{z} & o_{z} & a_{z} & p_{z} \\ 0 & 0 & 0 & 1 \end{bmatrix}$

其中前3x3表示旋转矩阵：

后4x1表示平移矩阵：

$P=\begin{vmatrix} p_{x}\\ p_{y}\\ p_{z}\\ 1 \end{vmatrix}$

合在一起可以简写为：

$T=RP$

齐次矩阵=旋转矩阵*平移矩阵

以上公式就可以完全描述出机器人单个关节在笛卡尔坐标系下的任意距离移动和角度旋转了，接下来我们就开始证明。

2.齐次矩阵的数学推导

2.1.旋转矩阵

第一步：我们来证明单个机器人关节旋转矩阵的坐标映射，由于在平面上坐标的Z轴是垂直于纸面，所以不需要绘制，再接下来的证明，也就默认代表基于Z轴来旋转。

我们画了一个红色的坐标系 $O_{1}$ ，在这个坐标系上面有一个 $P_{1}$ 的矢量，坐标的位置对应 $y_{1}$ 和 $x_{1}$

我们用矩阵的描述方式来表达 $P_{1}$ 的位置： $P_{1} = \begin{bmatrix} x_{1}\\ y_{1}\\ z_{1} \end{bmatrix}$

之后我们在同圆心的位置画一个 $O_{2}$ 坐标系，用蓝色的笔来标注，同时旋转了 $\theta$ 角度

这个时候 $P_{1}$ 在坐标系 $O_{2}$ 上面的坐标描述就等于

$P_{1}=\begin{bmatrix} x_{2}\\ y_{2}\\ z_{2} \end{bmatrix}$

那么问题就来了，当我们已知P1在 $O_{2}$ 坐标系上面的位置矢量和旋转角度的时候，怎么来求得他在 $O_{1}$ 坐标系上面的位置信息？

这个时候我们可以借助三角函数。

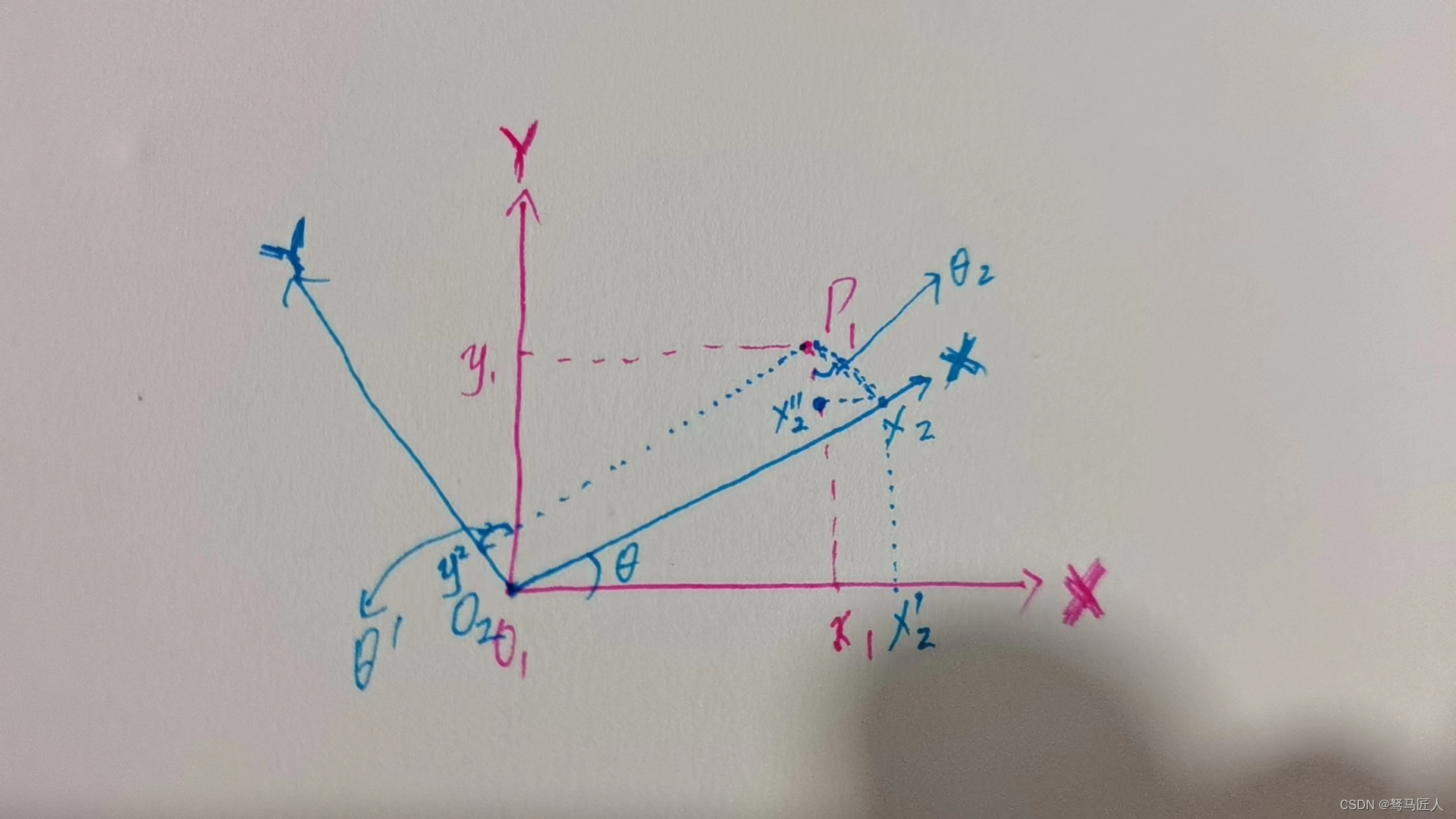
我们再把图片细化，我们要求得 $P_{1}$ 在 $O_{1}$ 中的位置，我们只需要去求 $x_{1} =\vec{O_{1}x_{1}}$ 和 $y_{1}=\vec{O_{1}y_{1}}$ 的长度即可。

画如下图片，我们吧 $x_{2}$ 做一个垂直线，垂点是 $x_{2}^{'}$ ：

如果求 $\vec{O_{1}x_{1}}$ 的长度，公式为：

$x_{1}=\vec{O_{1}x_{1}}=\vec{O_{1}x_{2}^{'}}-\vec{x_{1}x_{2}^{'}}$

其中：

$\vec{O_{1}x_{2}^{'}}=x_{2}\cos\theta$

$\vec{x_{1}x_{2}^{'}}=y_{2}\sin\theta$ (原因如下图，因为 $\theta = \theta^{'}=\theta_{2}$ ；原因是因为图纸标注的两个小三角形三边平行，根据平行线定理得知两个小三角形内角也相等，所以 $\theta ^{'} = \theta_{2}$ ；由于 $\theta = \theta ^{'}$ 是已知的，所以 $\theta = \theta^{'}=\theta_{2}$ ，设斜边= $\vec{P_{1}x_{2}}=y_{2}$ ；那么得到结论 $\vec{x_{1}x_{2}^{'}}=y_{2}\sin\theta$ )

带入公式得到：

$x_{1}=\vec{O_{1}x_{1}}=x_{2}\cos\theta-y_{2}\sin\theta$

根据下图同样的方式推导：

$y_{1}=\vec{P_{1}x_{1}}=\vec{P_{1}x_{2}^{''}}+\vec{x_{2}^{''}x_{1}}$

其中：

$\vec{P_{1}x_{2}^{''}} = y_{2}\cos\theta$

$\vec{x_{2}^{''}x_{1}}=\vec{x_{2}x_{2}^{'}}=x_{2}\sin\theta$

代入公式得最终结果：

$y_{1}=\vec{P_{1}x_{1}}=x_{2}\sin\theta+y_{2}cos\theta$

整理如下公式：

$x_{1}=x_{2}\cos\theta-y_{2}\sin\theta$

$y_{1}=x_{2}\sin\theta+y_{2}\cos\theta$

$z_{1}=z_{2}$ (由于Z轴原点没有变化，那么他们始终相等)

以上我们就推导出了沿着Z轴旋转 $\theta$ 角度，在坐标系 $O_{1}$ 和坐标系 $O_{2}$ 之间的一个计算公式，我们再把以上方程组转化为一个3x3的矩阵，用来描述 $P_{1}$ 位置在两个坐标系之间的关系：

$P_{1}=\begin{bmatrix} x_{1}\\ y_{1}\\ z_{1} \end{bmatrix}= \begin{bmatrix} cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0 & 0& 1 \end{bmatrix}\begin{bmatrix} x_{2}\\ y_{2}\\ z_{2} \end{bmatrix}$

其中R即可表示一个旋转矩阵，也可以称作是一个沿着z轴旋转的算子

$R_{z}(\theta)= \begin{bmatrix} cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0 & 0& 1 \end{bmatrix}$

通过以上同样的方式，我们可以推算出沿着y轴和x轴，过程类似，我就不推算了,可自行推导，直接写结果：

$R_{y}(\theta)= \begin{bmatrix} cos\theta & 0 & sin\theta\\ 0& 1 & 0\\ -sin\theta & 0& cos\theta \end{bmatrix}$

$R_{x}(\theta)= \begin{bmatrix} 1 & 0 & 0\\ 0& cos\theta & -sin\theta\\ 0 & sin\theta & cos\theta \end{bmatrix}$

2.2.平移矩阵

相对于平移矩阵，就比旋转矩阵简单多了，上面我们介绍的都是基于两个坐标系原点一样的情况下进行，我们就忽略了位置信息，接下来我们开始让坐标系 $O_{2}$ 的原点沿着坐标系 $O_{1}$ 原点移动 $x_{0}$ 和 $y_{0}$ 的距离。如下图：

那么我们只需要在以上推导出来的公式上加上 $x_{0}$ 和 $y_{0}$ 即可：

$x_{1}=x_{2}\cos\theta-y_{2}\sin\theta+x_{0}$

$y_{1}=x_{2}\sin\theta+y_{2}\cos\theta+y_{0}$

$z_{1}=z_{2}$ (Z轴距离始终相等)

那么上述公式，就升级4x4矩阵形式：

$P_{1}=\begin{bmatrix} x_{1}\\ y_{1}\\ z_{1}\\ 1\end{bmatrix}= \begin{bmatrix} cos\theta & -sin\theta & 0& x_{0}\\ sin\theta & cos\theta & 0& y_{0}\\ 0 & 0& 1 & z_{0}\\0 & 0& 0& 1\end{bmatrix}\begin{bmatrix} x_{2}\\ y_{2}\\ z_{2} \\ 1\end{bmatrix}$