基于布鲁斯特效应的模拟计算

这个方法是基于格林函数法，不同于前面的超表面方法需要一个傅里叶变换子块，逆傅里叶变换子块，中间的滤波子块，而是直接通过适当设计沿x轴和y轴的多层板实现数学计算。所有层都是横向同质的，但可以纵向不同质。但格林函数方法有两个主要缺点，一是格林函数需要在空间傅里叶变换域具有偶次对称性，二是相对介电常数和每层的厚度是通过快速合成方法计算的，这将会导致不切实际的数值。

 奇格林函数的功能可以通过旋转装置实现，即通过斜入射实现，在这篇文章中通过使用布鲁斯特效应的界面来解决第二个缺点，从而实现基本的差分。正在研究的系统如下图所示，可以看到通过将装置旋转替代一个垂直射入的情况，然后旋转之后，坐标系就有一个转换。

图2 通过旋转多层板来获得偶对称格林函数

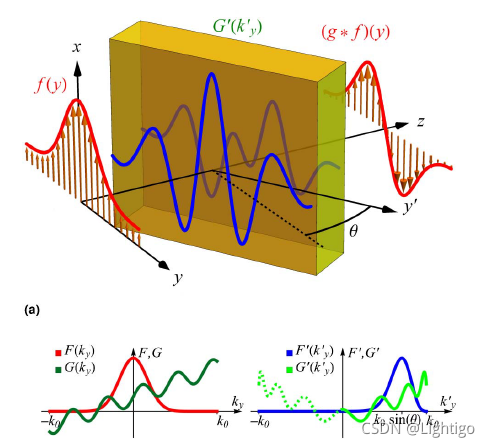
 上式就是讲y方向的波矢在坐标系变换后的转换。相应的格林函数（传递函数）也会有一个转换，转换后的图形如图2所示，可以看到转换后对图像信息的作用和之前是一样的。

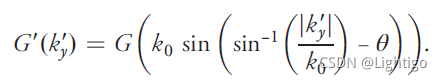
下图是他所研究的结构，只由一个界面组成，一个任意波形的光束斜入射到这个自由空间和折射率为n的材料的交界面上，然后由于一阶导数的傅里叶变换是ik，在Ky=0时，Ky'=K0*sin（theta），传递函数必须是0，在进行坐标转换后也是0，但是不管是TE模还是TM模都没有0传递系数，所以本篇文章利用TM模在布鲁斯特角入射时的反射系数是0，利用这一特点实现一阶导数的传递函数。

 将格林函数展开：

 然后第一项=0，然后令n=2.1，布鲁斯特角为64.6°时，代入得到下图所示的格林函数图，绿色的线代表准确的格林函数，橙色的线代表是通过泰勒级数展开的近似，在ky=0附近，近似值还是比较准确的。

然后下图分析了在误差率为不超过10%的情况下的最大带宽与折射率的关系。

总结：使用旋转结构打破反射对称性实现奇格林函数的功能，基于这些旋转配置利用布鲁斯特效应实现对导数空间的微分，然后可以通过级联一阶的微分来实现高阶的微分。