第四章 组合逻辑电路
考纲:
- 电路分析
- 电路设计
- 竞争与险象的产生、判断和消除
数字系统中的逻辑电路按其是否具有记忆功能分为组合逻辑电路和时序逻辑电路两大类型。本章讨论组合逻辑电路,他通常以以下形式出现
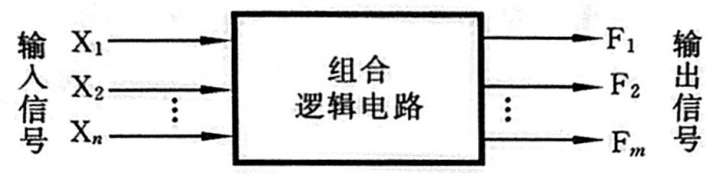
电路分析
所谓电路分析,就是给你一个电路图,然后问你几个问题,比如这个电路实现了什么?能不能画他的波形图之类的,为了能准确分析,我们通常按照下面几个步骤走:
-
根据逻辑电路图写出输出函数表达式
要看懂电路图,首先要明白电路图画了什么:
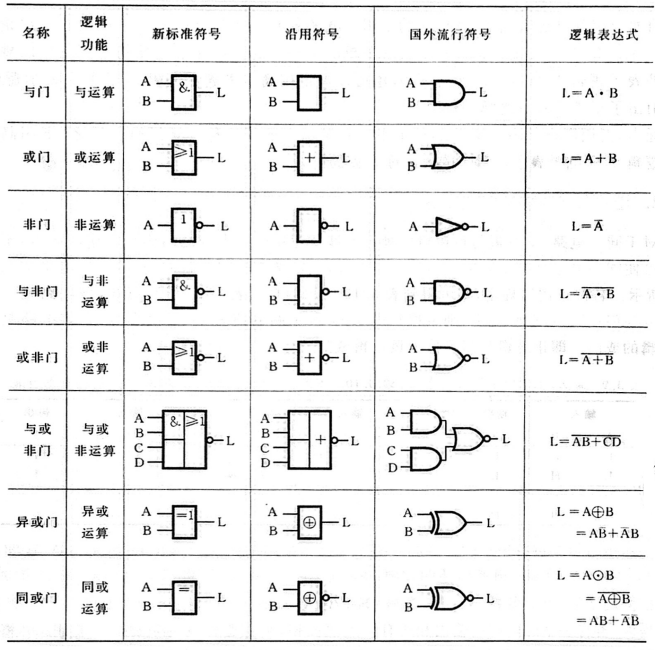
注意分析的时候,不要一下子全部写出来,要一个一个写,然后最后拼起来
-
化简输出函数表达式
如果你觉得可以硬列的话可以不化简(笑)
-
列出输出函数真值表
-
功能评述
【例】写出组合电路的输出函数及其真值表
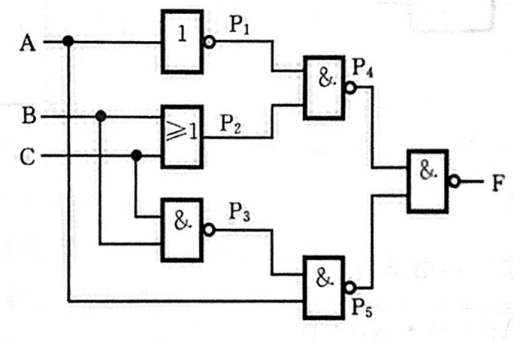
【解】
-
根据逻辑电路图写出输出函数表达式
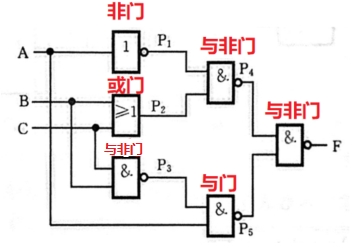
P 1 = A ‾ P 2 = B + C P 3 = B C ‾ P 4 = P 1 ⋅ P 2 ‾ = A ‾ ( B + C ) ‾ P 5 = A ⋅ P 3 ‾ = A B C ‾ ‾ F = P 4 ⋅ P 5 ‾ = A ‾ ( B + C ) ‾ ⋅ A B C ‾ ‾ ‾ \begin{array}{ll} \mathrm{P}_1=\overline{\mathrm{A}} & \mathrm{P}_2=\mathrm{B}+\mathrm{C} \\ \mathrm{P}_3=\overline{\mathrm{BC}} & \mathrm{P}_4=\overline{\mathrm{P}_1 \cdot \mathrm{P}_2}=\overline{\overline{\mathrm{A}}(\mathrm{B}+\mathrm{C})} \\ \mathrm{P}_5=\overline{\mathrm{A} \cdot \mathrm{P}_3}=\overline{\mathrm{A} \overline{\mathrm{BC}}} & \mathrm{F}=\overline{\mathrm{P}_4 \cdot \mathrm{P}_5}=\overline{\overline{\overline{\mathrm{A}}(\mathrm{B}+\mathrm{C})} \cdot \overline{\mathrm{A} \overline{\mathrm{BC}}}} \end{array} P1=AP3=BCP5=A⋅P3=ABCP2=B+CP4=P1⋅P2=A(B+C)F=P4⋅P5=A(B+C)⋅ABC -
化简输出函数表达式
F = A ‾ ( B + C ) ‾ ⋅ A ⋅ B C ‾ ‾ ‾ = A ‾ ( B + C ) + A B C ‾ ( A ⋅ B ‾ = A ˉ + B ˉ ) = A ‾ B + A ‾ C + A B ‾ + A C ‾ ( 分配律 ) = A ⊕ B + A ⊕ C \begin{aligned} \mathrm{F} & =\overline{\overline{\overline{\mathrm{A}}(\mathrm{B}+\mathrm{C})} \cdot \overline{\mathrm{A} \cdot \overline{\mathrm{BC}}}} \\ & =\overline{\mathrm{A}}(\mathrm{B}+\mathrm{C})+\mathrm{A} \overline{\mathrm{BC}}&&(\overline{A \cdot B}=\bar{A}+\bar{B}) \\ & =\overline{\mathrm{A}} \mathrm{B}+\overline{\mathrm{A} }\mathrm{C}+\mathrm{A} \overline{\mathrm{B}}+\mathrm{A} \overline{\mathrm{C}}&&(\text{分配律}) \\ & =\mathrm{A} \oplus \mathrm{B}+\mathrm{A} \oplus \mathrm{C}&& \end{aligned} F=A(B+C)⋅A⋅BC=A(B+C)+ABC=AB+AC+AB+AC=A⊕B+A⊕C(A⋅B=Aˉ+Bˉ)(分配律) -
画真值表
A B C F 0 0 0 0 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 0 \begin{array}{ccc|c} \hline \mathrm{A} & \mathrm{B} & \mathrm{C} & \mathrm{F} \\ \hline 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ 0 & 1 & 0 & 1 \\ 0 & 1 & 1 & 1 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\ \hline \end{array} A00001111B00110011C01010101F01111110
电路设计
电路设计刚好是反过来的,先画真值表,然后按题目要求用卡诺图推出输出函数
- 看懂题意,给出逻辑描述
- 根据卡诺图求出最简表达式
- 根据题意转换逻辑函数
- 画出函数逻辑图
【例】设计一个3变量“多数表决电路”,要求只使用与非门
【解】所谓多数表决,就是少数服从多数,即“两个1以上就输出1”,根据这个思想可以列出真值表
A
B
C
F
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
1
1
1
0
1
1
1
1
1
\begin{array}{ccc|c} \hline \mathrm{A} & \mathrm{B} & \mathrm{C} & \mathrm{F} \\ \hline 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 1 & 1 & 1 \\ 1 & 0 & 0 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 \\ \hline \end{array}
A00001111B00110011C01010101F00010111
由此可以画出卡诺图
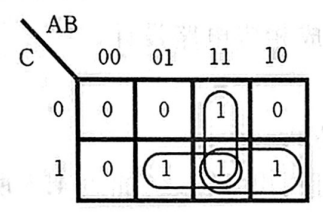
由此可以列出最简表达式
F
=
A
B
+
A
C
+
B
C
\mathrm{F=AB+AC+BC}
F=AB+AC+BC
然后可以对该表达式依据题意转换
F
(
A
,
B
,
C
)
=
A
B
+
A
C
+
A
C
‾
‾
=
A
B
‾
⋅
A
C
‾
⋅
B
C
‾
‾
F(A, B, C)=\overline{\overline{\mathrm{A B+A C+AC}}}=\overline{\overline{\mathrm{AB}} \cdot \overline{\mathrm{AC}} \cdot \overline{\mathrm{BC}}}
F(A,B,C)=AB+AC+AC=AB⋅AC⋅BC
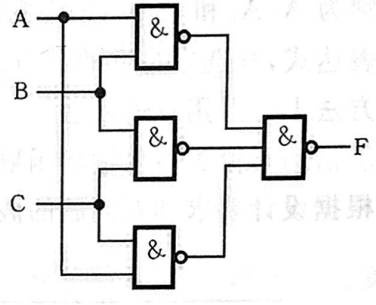
险象
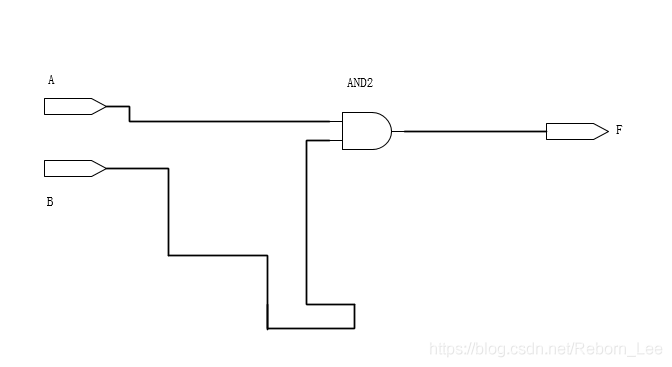
以该图为例,假设此时A是“0”,B是“1”,F应该是0。而某一瞬间A变成了“1”,B变成了“0”,由于A的线比较短,走的比较快,所以很短的时刻内,“A变1”的这个影响很快传到了AND门上,而“B变0”这个影响还没传到AND门上,于是造成了短暂的“F变1”现象,这就是险象。在短暂过后,B的影响传了过来,F变回了0
所谓的险象,可以理解为“本来应该是那样,但却有一瞬间反了过来"
判断方法
在一般情况下,我们不考虑线带来的延时问题,一般考虑每个门造成的时间差,即你可能会在题目里看到这种图:
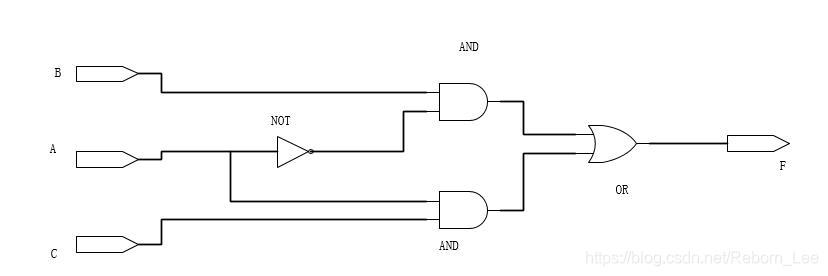
为了判断是否有险象,有两种方法,其中一种方法通常采用以下步骤:
- 确定考察变量“A”,然后列举其他变量的所有组合
- 判断每个组合下,考察变量“A”是否以“ A + A ˉ \mathrm{A+\bar{A}} A+Aˉ ” 或者 " A ⋅ A ˉ \mathrm{A\cdot\bar{A}} A⋅Aˉ" 的形式成双成对出现
- 如果是,则说明该变量有可能产生现象
判断时有个小技巧,如果某个变量 A \mathrm{A} A 在表达式中本就不同时存在 A \mathrm{A} A 和 A ˉ \mathrm{\bar{A}} Aˉ 那肯定不存在险象
【例】某组合电路的表达式为 F = A ˉ C ˉ + A ˉ B + A C \mathrm{F=\bar{A}\bar{C}+\bar{A}B+AC} F=AˉCˉ+AˉB+AC 判断是否产生现象
-
考察变量 A \mathrm{A} A
B C F 0 0 F = A ˉ 0 1 F = A 1 0 F = A ˉ 1 1 F = A + A ˉ \begin{array}{|c c|c|} \hline \mathrm{B} & \mathrm{C} & \mathrm{F} \\ \hline 0 & 0 & \mathrm{F}=\bar{\mathrm{A}} \\ 0 & 1 & \mathrm{F}={\mathrm{A}} \\ 1 & 0 & \mathrm{F}=\bar{\mathrm{A}} \\ 1 & 1 & \mathrm{F}=\mathrm{A}+\bar{\mathrm{A}} \\ \hline \end{array} B0011C0101FF=AˉF=AF=AˉF=A+Aˉ
因此 A \mathrm{A} A 有可能产生险象 -
考察变量 C \mathrm{C} C
A B F 0 0 F = C ˉ 0 1 F = 1 1 0 F = C 1 1 F = C \begin{array}{|c c|c|} \hline \mathrm{A} & \mathrm{B} & \mathrm{F} \\ \hline 0 & 0 & \mathrm{F}=\bar{\mathrm{C}} \\ 0 & 1 & \mathrm{F}=1 \\ 1 & 0 & \mathrm{F}={\mathrm{C}} \\ 1 & 1 & \mathrm{F}={\mathrm{C}} \\ \hline \end{array} A0011B0101FF=CˉF=1F=CF=C
因此 C \mathrm{C} C 不会产生险象
除了逐一判断外,还可以使用卡诺图判断。
卡诺图判断法是看画出来的卡诺圈中是否存在"相切"现象,如果存在,则说明有险象,相切中变的那个变量就是产生险象的变量
【例】判断函数表达式 F = A ˉ D + A ˉ C + A B C ˉ \mathrm{F=\bar{A}D+\bar{A}C+AB\bar{C}} F=AˉD+AˉC+ABCˉ 是否有险象
【解】存在险象
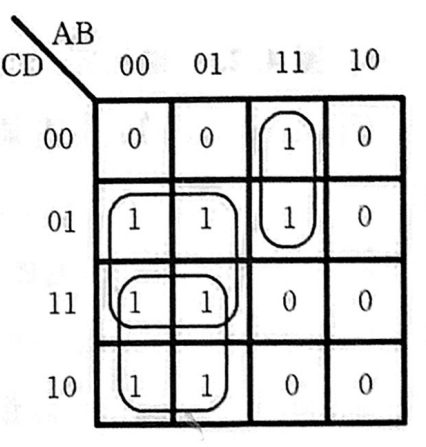
将 B = D = 1 , C = 0 \mathrm{B=D=1,C=0} B=D=1,C=0 代入得: F = A ˉ + A \mathrm{F=\bar{A}+A} F=Aˉ+A ,变量 A \mathrm{A} A 可能产生险象
消除方法
本篇只介绍一个方法:增加冗余项的方法
回到刚才的例子中, 某组合电路的表达式为
F
=
A
ˉ
C
ˉ
+
A
ˉ
B
+
A
C
\mathrm{F=\bar{A}\bar{C}+\bar{A}B+AC}
F=AˉCˉ+AˉB+AC ,
A
\mathrm{A}
A 可能产生现象
B
C
F
0
0
F
=
A
ˉ
0
1
F
=
A
1
0
F
=
A
ˉ
1
1
F
=
A
+
A
ˉ
\begin{array}{|c c|c|} \hline \mathrm{B} & \mathrm{C} & \mathrm{F} \\ \hline 0 & 0 & \mathrm{F}=\bar{\mathrm{A}} \\ 0 & 1 & \mathrm{F}={\mathrm{A}} \\ 1 & 0 & \mathrm{F}=\bar{\mathrm{A}} \\ 1 & 1 & \mathrm{F}=\mathrm{A}+\bar{\mathrm{A}} \\ \hline \end{array}
B0011C0101FF=AˉF=AF=AˉF=A+Aˉ
所谓险象,就是在
B
=
C
=
1
\mathrm{B=C=1}
B=C=1 时本来按表达式
F
=
A
+
A
ˉ
\mathrm{F}=\mathrm{A}+\bar{\mathrm{A}}
F=A+Aˉ 应该是1才对,但却有一瞬间变成了 “0”,因此解决方法就是针对这个情况加一个必然为“1” 的项,于是原式变成了:
F
=
A
ˉ
C
ˉ
+
A
ˉ
B
+
A
C
+
B
C
\mathrm{F=\bar{A}\bar{C}+\bar{A}B+AC}+\mathrm{BC}
F=AˉCˉ+AˉB+AC+BC
对于卡诺图,要想他不出现“相切”的情况,那就再加一个冗余的卡诺圈:
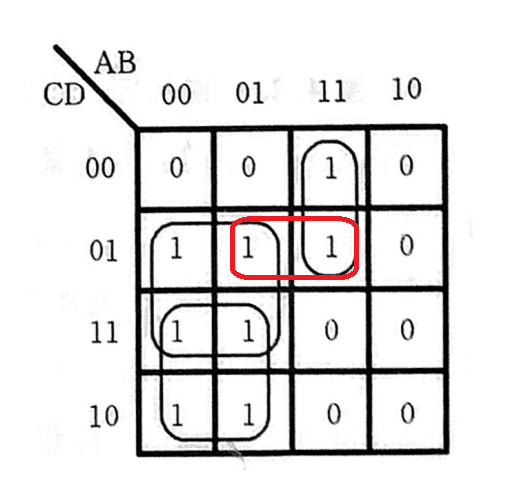
于是原式
F
=
A
ˉ
D
+
A
ˉ
C
+
A
B
C
ˉ
\mathrm{F=\bar{A}D+\bar{A}C+AB\bar{C}}
F=AˉD+AˉC+ABCˉ 变成了:
F
=
A
ˉ
D
+
A
ˉ
C
+
A
B
C
ˉ
+
B
C
ˉ
D
\mathrm{F=\bar{A}D+\bar{A}C+AB\bar{C}+B\bar{C}D}
F=AˉD+AˉC+ABCˉ+BCˉD
导论 时序逻辑电路
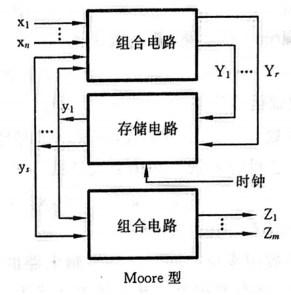
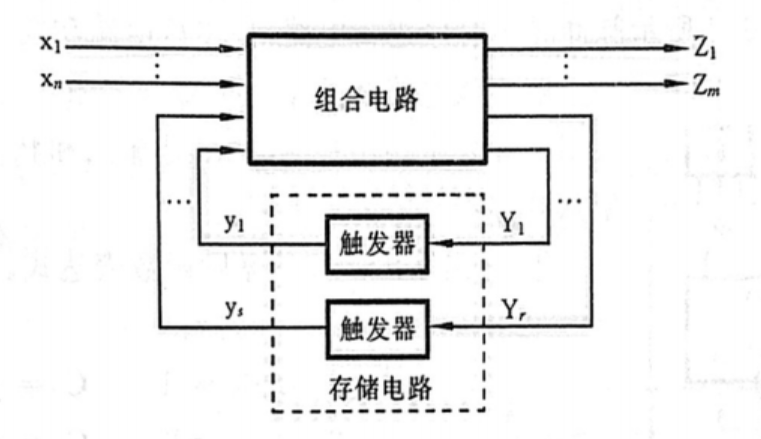
时序逻辑电路的结构通常如下
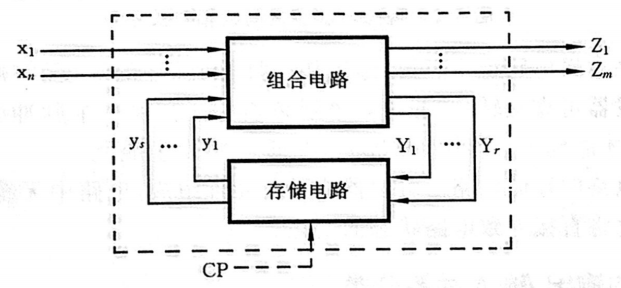
即稳定输出信号不仅与该电路该时刻的输入信号有关,而且与电路过去的输入信号有关,所谓“与电路过去的输入信号有关” 就是将过去的输入信号存储在“存储电路”中,然后作为输入喂给组合电路。
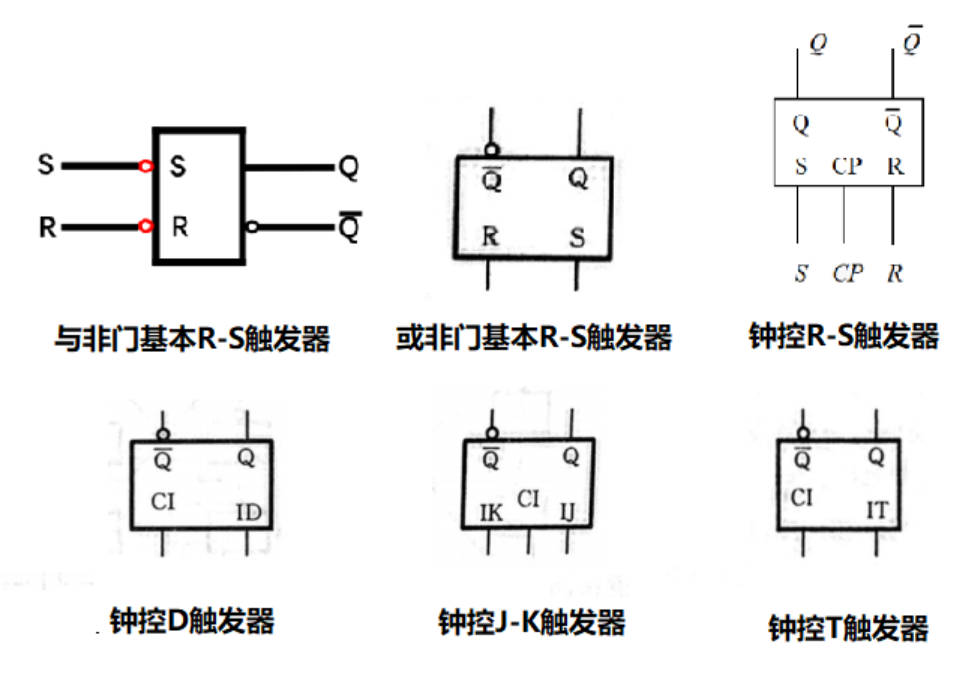
而存储电路,顾名思义就是有记忆的电路,那什么是有记忆的电路呢?没错,就是触发器,下文可能会出现各种各样的触发器,因此我把图再放一次方便大家查阅
电路分类:同步与异步
同步电路是那些由时钟信号驱动的电路。在同步电路中,所有操作都与特定的时钟脉冲同步。这意味着所有的状态变化(例如,存储器中的数据或逻辑门的输出)都是在特定的时钟周期发生的。同步电路的一个主要优点是设计相对简单,因为你只需要考虑特定的时钟周期。然而,同步电路的一个主要缺点是它们通常需要更多的功耗,因为即使电路的一部分没有活动,时钟也会持续工作。
异步电路不依赖于统一的时钟信号来驱动其操作。相反,它们通常使用一种被称为握手的协议,其中一个部分的电路将发送一个信号给另一个部分,告知它何时开始或结束一个操作。这使得异步电路能够在不需要时钟的情况下工作,这可以降低功耗,并允许电路以最大速度运行。然而,异步电路的设计和验证通常比同步电路更复杂,因为你必须考虑所有可能的信号到达和离开的时间。
所以,同步电路和异步电路的主要区别在于它们的操作是否由统一的时钟信号控制。同步电路由时钟驱动,而异步电路则不是。这影响了它们的设计、性能、功耗,以及所需要的设计和验证工作量。
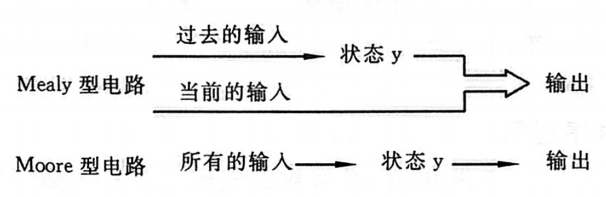
电路种类:Mealy与Moore
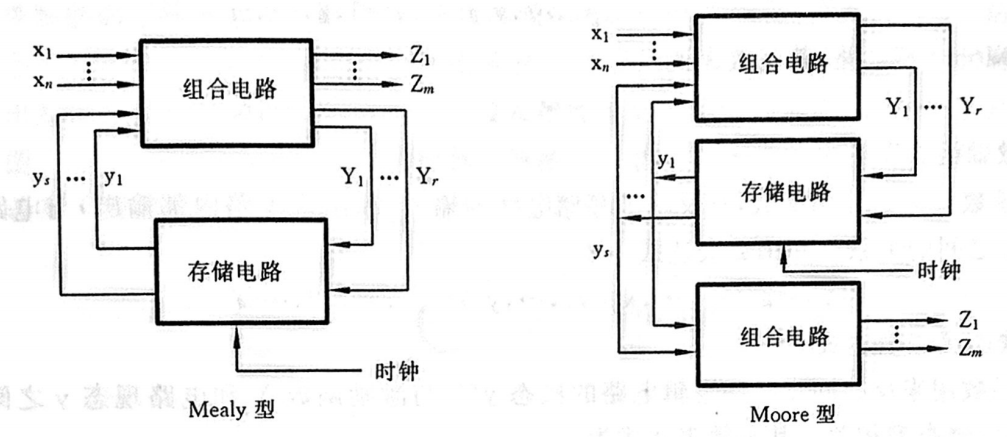
根据电路的输出是否与输人直接相关,可以分为 Mealy(米利)型和 Moore(穆尔)型两种不同模型的时序逻辑电路。若时序逻辑电路的输出是电路输入和电路状态的函数,则称为Mealy型时序逻辑电路;若时序逻辑电路的输出仅仅是电路状态的函数,则称为Moore型时序逻辑电路。
输入信号的种类:电平与脉冲
在时序逻辑电路中,存在两种常见的类型:电平型(Level-Triggered)和脉冲型(Edge-Triggered)。
- 电平型(Level-Triggered):在电平型的触发方式中,设备在时钟信号的整个高电平或低电平阶段都可能会被触发。也就是说,只要时钟信号在一个特定的水平,就可能产生变化。例如,电平型触发器可能在时钟信号的高电平期间响应输入信号的变化。这就意味着在整个高电平期间,只要输入发生变化,触发器就会响应。
- 脉冲型(Edge-Triggered):相比之下,脉冲型触发设备只在时钟信号的上升沿或下降沿响应。在其他所有的时间里,设备的状态都保持不变,不会对输入信号的变化做出反应。例如,一个上升沿触发的触发器只在时钟信号从低电平变到高电平的瞬间响应输入信号的变化。
在数字电子系统中,上升沿和下降沿描述的是一个信号状态从低到高(上升沿)或者从高到低(下降沿)的转变。
- 上升沿:当一个数字信号从逻辑低电平跳变到逻辑高电平时,这个跳变的瞬间被称为"上升沿"。这个名字来源于如果你在示波器上观察这个信号,你会看到电压从低电平"上升"到高电平,这个跳变的瞬间就像是一个"沿"。
- 下降沿:相反地,当一个数字信号从逻辑高电平跳变到逻辑低电平时,这个跳变的瞬间被称为"下降沿"。这也是因为如果你在示波器上观察这个信号,你会看到电压从高电平"下降"到低电平,这个跳变的瞬间看起来就像是一个"沿"。
电路的描述方法
-
输出函数表达式
对于 Mealy 型电路, 其函数表达式为
Z i = f i ( x 1 , ⋯ , x n , y 1 , ⋯ , y s ) i = 1 , 2 , ⋯ , m \mathrm{Z}_i=\mathrm{f}_i\left(\mathrm{x}_1, \cdots, \mathrm{x}_n, \mathrm{y}_1, \cdots, \mathrm{y}_s\right) \quad i=1,2, \cdots, m Zi=fi(x1,⋯,xn,y1,⋯,ys)i=1,2,⋯,m
对于 Moore 型电路, 其函数表达式为
Z i = f i ( y 1 , ⋯ , y s ) i = 1 , 2 , ⋯ , m \mathrm{Z}_i=\mathrm{f}_i\left(\mathrm{y}_1, \cdots, \mathrm{y}_s\right) \quad i=1,2, \cdots, m Zi=fi(y1,⋯,ys)i=1,2,⋯,m -
激励函数与激励图
激励函数又称为控制函数, 它反映了存储电路(触发器)的输入 Y Y Y (组合电路内部输出)与电路输入 x \mathrm{x} x 和状态 y \mathrm{y} y 之间的关系。其函数表达式为
Y j = g j ( x 1 , ⋯ , x n , y 1 , ⋯ , y s ) j = 1 , 2 , ⋯ , r \mathrm{Y}_j=\mathrm{g}_j\left(\mathrm{x}_1, \cdots, \mathrm{x}_n, \mathrm{y}_1, \cdots, \mathrm{y}_s\right) \quad j=1,2, \cdots, r Yj=gj(x1,⋯,xn,y1,⋯,ys)j=1,2,⋯,r
对于激励函数,还可以画他的激励图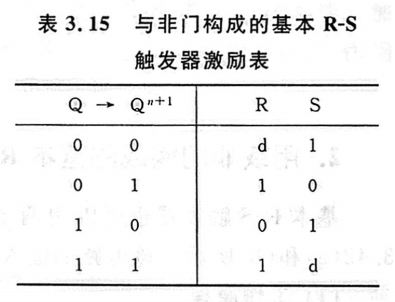
其中“d”表示不确定
-
状态表与状态图
状态表反映了触发器在输人作用下现态 Q n \mathrm{Q^{n}} Qn 与次态 Q n + 1 \mathrm{Q^{n+1}} Qn+1之间的转移关系
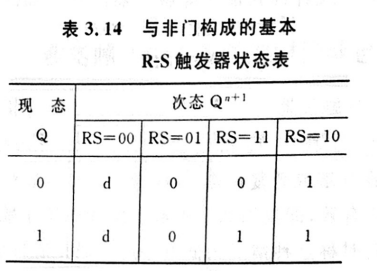
状态图是一种反映触发器两种状态之间转移关系的有向图,又称为状态转移图,两个圆圈分别代表触发器的两个稳定状态,箭头表示在输入信号作用下状态转移的方向,箭头旁边的标注表示状态转移的条件。
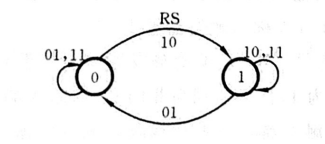
-
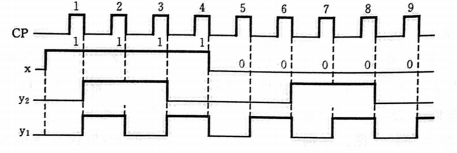
时间图
时间图其实就是在做实验的时候要交的那张拍下来的图。在时间图里面,CP时钟信号是固定的0101循环,x输入由自己指定,然后根据状态表或者状态图画出来,具体过程在后面的例题会讲解。
第五章 同步时序逻辑电路
电路分析
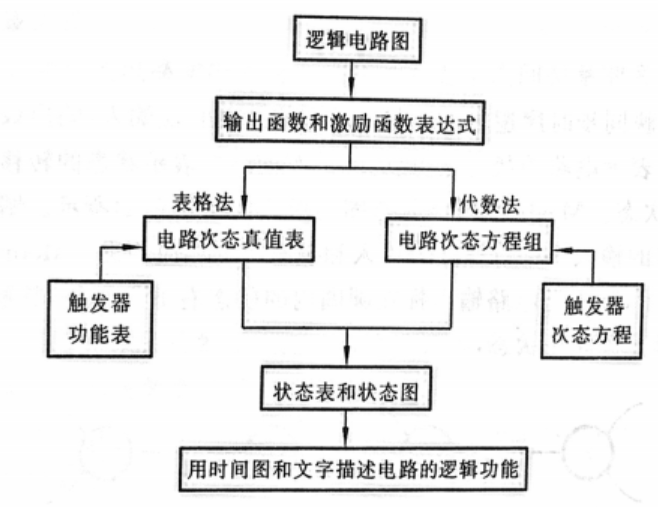
【例】用表格法分析同步时序逻辑电路。
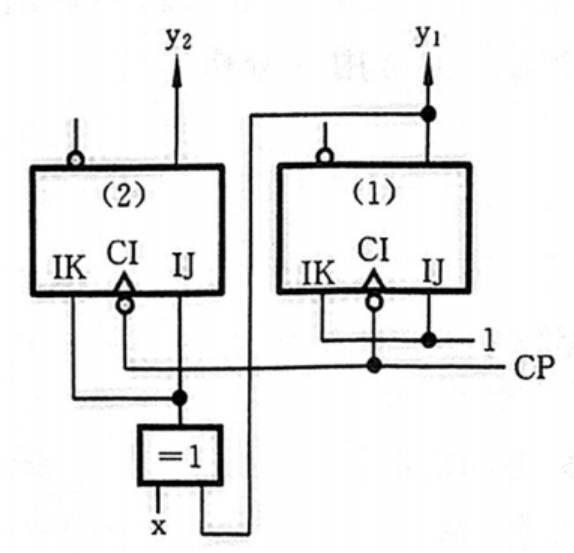
【解】我们先来分析电路:首先要搞清楚存储电路和组合电路分别是哪个,找到输入 x \mathrm{x} x 和 输出 Z \mathrm{Z} Z

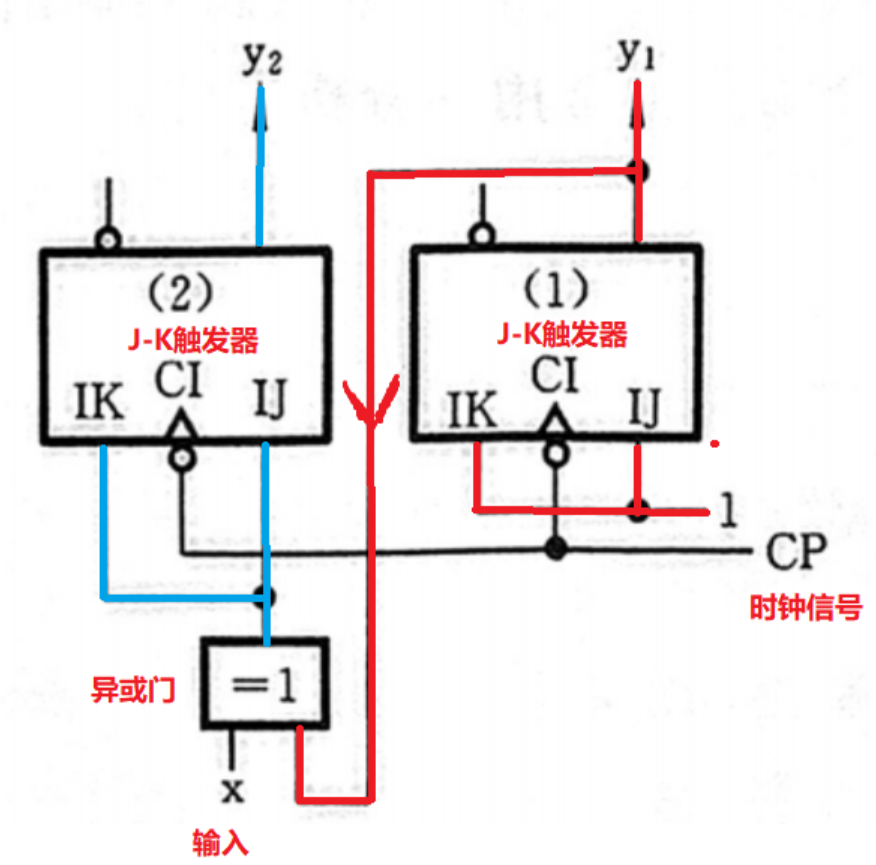
该电路有两个钟控J-K触发器组成存储电路,一个异或门组成组合电路,由于触发器(1)的输出同时作为输入,因此他是一个“输出是电路状态的电路”
,即他是一个Moore型电路
然后我们再来分析激励函数,可以看出,触发器(1)的输入JK都是1
J
1
=
K
1
=
1
\mathrm{J_1=K_1 =1}
J1=K1=1
而触发器(2)的JK由异或门决定,异或门的输入为
x
\mathrm{x}
x 和触发器(1)的输出
y
1
\mathrm{y_1}
y1
J
2
=
K
2
=
x
⊕
y
1
\mathrm{J_2=K_2=x \oplus y_1}
J2=K2=x⊕y1
然后我们可以列次态真值表,会改变的量有“输入
x
\mathrm{x}
x ”和“现态
y
1
,
y
2
\mathrm{y_1 ,y_2}
y1,y2” ,同时需要描述每个触发器的输入
J
,
K
\mathrm{J,K }
J,K ,最后得到次态
y
1
n
+
1
,
y
2
n
+
1
\mathrm{y_1^{n+1} ,y_2^{n+1}}
y1n+1,y2n+1
输入
现
态
激励
函数
次
态
x
y
2
y
1
J
2
K
2
J
1
K
1
y
2
n
+
1
y
1
n
+
1
\begin{array}{c|cc|cccc|ccc} \hline \text { 输入 } & \text { 现 } & \text { 态 } &&{\text { 激励 }}& {\text { 函数 }} & & \text { 次 }&\text { 态 } \\ \mathrm{x} & \mathrm{y}_2 & \mathrm{y}_1 & \mathrm{~J}_2 & \mathrm{~K}_2 & \mathrm{~J}_1 & \mathrm{~K}_1 & \mathrm{y}_2^{n+1} & \mathrm{y}_1^{n+1} \\ \hline \end{array}
输入 x 现 y2 态 y1 J2 激励 K2 函数 J1 K1 次 y2n+1 态 y1n+1
需要明确的是,输入和现态的可能性是有限的,是可以一次性通过“二进制法”列举出来的
输入
现
态
激励
函数
次
态
x
y
2
y
1
J
2
K
2
J
1
K
1
y
2
n
+
1
y
1
n
+
1
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
\begin{array}{c|cc|cccc|ccc} \hline \text { 输入 } & \text { 现 } & \text { 态 } &&{\text { 激励 }}& {\text { 函数 }} & & \text { 次 }&\text { 态 } \\ \mathrm{x} & \mathrm{y}_2 & \mathrm{y}_1 & \mathrm{~J}_2 & \mathrm{~K}_2 & \mathrm{~J}_1 & \mathrm{~K}_1 & \mathrm{y}_2^{n+1} & \mathrm{y}_1^{n+1} \\ \hline 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 0 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\ \hline \end{array}
输入 x00001111 现 y200110011 态 y101010101 J2 激励 K2 函数 J1 K1 次 y2n+1 态 y1n+1
然后我们再来填激励函数,根据上面得到的两个公式
J
1
=
K
1
=
1
J
2
=
K
2
=
x
⊕
y
1
\mathrm{J_1=K_1 =1} \\ \mathrm{J_2=K_2=x \oplus y_1}
J1=K1=1J2=K2=x⊕y1
输入 现 态 激励 函数 次 态 x y 2 y 1 J 2 K 2 J 1 K 1 y 2 n + 1 y 1 n + 1 0 0 0 0 0 1 1 0 0 1 1 1 1 1 0 1 0 0 0 1 1 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0 1 0 0 1 1 1 1 0 1 1 1 1 1 1 1 0 0 1 1 \begin{array}{c|cc|cccc|ccc} \hline \text { 输入 } & \text { 现 } & \text { 态 } &&{\text { 激励 }}& {\text { 函数 }} & & \text { 次 }&\text { 态 } \\ \mathrm{x} & \mathrm{y}_2 & \mathrm{y}_1 & \mathrm{~J}_2 & \mathrm{~K}_2 & \mathrm{~J}_1 & \mathrm{~K}_1 & \mathrm{y}_2^{n+1} & \mathrm{y}_1^{n+1} \\ \hline 0 & 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 1 & 1 & 1 & 1 \\ 0 & 1 & 0 & 0 & 0 & 1 & 1 \\ 0 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 0 & 0 & 1 & 1 & 1 & 1 \\ 1 & 0 & 1 & 0 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 0 & 0 & 1 & 1 \\ \hline \end{array} 输入 x00001111 现 y200110011 态 y101010101 J201011010 激励 K201011010 函数 J111111111 K111111111 次 y2n+1 态 y1n+1
还记得鸡哥公式吗?“全0不变,全1翻转,一正一负看鸡哥”,对着这个公式就能写出次态
输入
现
态
激励
函数
次
态
x
y
2
y
1
J
2
K
2
J
1
K
1
y
2
n
+
1
y
1
n
+
1
0
0
0
0
0
1
1
0
1
0
0
1
1
1
1
1
1
0
0
1
0
0
0
1
1
1
1
0
1
1
1
1
1
1
0
0
1
0
0
1
1
1
1
1
1
1
0
1
0
0
1
1
0
0
1
1
0
1
1
1
1
0
1
1
1
1
0
0
1
1
1
0
\begin{array}{c|cc|cccc|ccc} \hline \text { 输入 } & \text { 现 } & \text { 态 } &&{\text { 激励 }}& {\text { 函数 }} & & \text { 次 }&\text { 态 } \\ \mathrm{x} & \mathrm{y}_2 & \mathrm{y}_1 & \mathrm{~J}_2 & \mathrm{~K}_2 & \mathrm{~J}_1 & \mathrm{~K}_1 & \mathrm{y}_2^{n+1} & \mathrm{y}_1^{n+1} \\ \hline 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 & 1 & 1 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 0 & 1 & 0 & 0 & 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 1 & 1 & 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 & 0 & 1 & 1 & 1 & 0 \\ \hline \end{array}
输入 x00001111 现 y200110011 态 y101010101 J201011010 激励 K201011010 函数 J111111111 K111111111 次 y2n+101101001 态 y1n+110101010
然后我们就能画状态图了,首先画状态表,状态表的画法是:总的来说是“现态→次态”表,要在表中指明是什么发生变化导致的(这里是
x
\mathrm{x}
x)
现
态
y
2
n
+
1
y
1
n
+
1
y
2
n
+
1
y
1
n
+
1
y
2
y
1
x
=
0
x
=
1
0
0
0
1
1
1
0
1
1
0
0
0
1
0
1
1
0
1
1
1
0
0
1
0
\begin{array}{|cc|cc|cc|} \hline 现&态 &y_2^{n+1} &y_1^{n+1}&y_2^{n+1}&y_1^{n+1}\\ y_2& y_1 &x=0 &&x=1 \\ \hline 0 & 0 & 0 & 1 & 1 & 1 \\ \hline 0 & 1 & 1 & 0 & 0 & 0 \\ \hline 1 & 0 & 1 & 1 & 0 & 1 \\ \hline 1 & 1 & 0 & 0 & 1 & 0 \\ \hline \end{array}
现y20011态y10101y2n+1x=00110y1n+11010y2n+1x=11001y1n+11010
再来画状态图
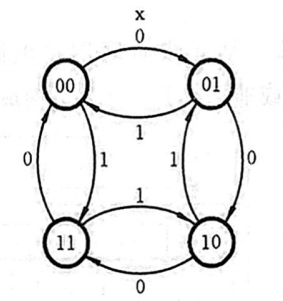
可以看出,当电路输入 x = 0 x=0 x=0 时, 可逆计数器进行加 1 计数, 其计数序列为
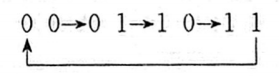
当输入 x = 1 x=1 x=1 时, 可逆计数器进行减 1 计数, 其计数序列为
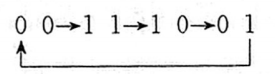
因此该电路实现了一个“二进制可逆计数器”
根据状态图,可以设定输入为 11110000 11110000 11110000 可以画出时间图
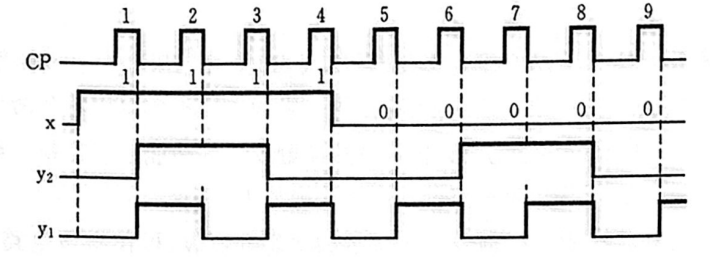
这里有一个细节:CP为0时次态不发生改变(JK触发器的特性),在CP为1后发生改变
【例】分析电路,回答下列问题:
(1) 图⽰电路中采⽤什么触发⽅式; (2) 分析下图所⽰时序逻辑电路,并指出其逻辑功能; (3) 设触发器初态为0,画出在CP脉冲下Q0和Q1的波形。
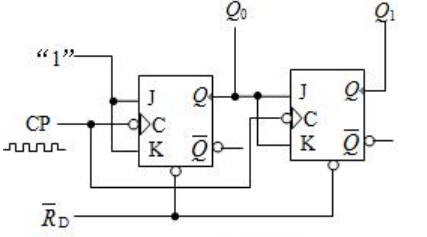
【解】老样子,先分析下
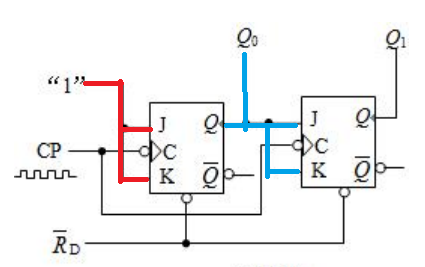
存储电路是两个J-K触发器,而
J
\mathrm{J}
J 和
K
\mathrm{K}
K 连在一起组成了
T
\mathrm{T }
T 触发器,从图上看,他是下降沿触发,对两个触发器可以写出激励函数
J
0
=
K
0
=
1
J
0
=
K
0
=
Q
0
\begin{aligned} \mathrm{J_0 =K_0 }&=1 \\ \mathrm{J_0 =K_0 }&=Q_0 \end{aligned}
J0=K0J0=K0=1=Q0
于是可以作次态真值表
现
态
激励
函数
次
态
Q
0
Q
1
J
0
K
0
J
1
K
1
Q
0
n
+
1
Q
1
n
+
1
0
0
1
1
0
0
1
0
0
1
1
1
0
0
1
1
1
0
1
1
1
1
0
1
1
1
1
1
1
1
0
0
\begin{array}{cc|cccc|ccc} \hline \text { 现 } & \text { 态 } &&{\text { 激励 }}& {\text { 函数 }} & & \text { 次 }&\text { 态 } \\ \mathrm{Q}_0 & \mathrm{Q}_1 & \mathrm{~J}_0 & \mathrm{~K}_0 & \mathrm{~J}_1 & \mathrm{~K}_1 & \mathrm{Q}_0^{n+1} & \mathrm{Q}_1^{n+1} \\ \hline 0 & 0 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 1 & 1 & 0 & 0 & 1 & 1 \\ 1 & 0 & 1 & 1 & 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 0 & 0 \\ \hline \end{array}
现 Q00011 态 Q10101 J01111 激励 K01111 函数 J10011 K10011 次 Q0n+11100 态 Q1n+10110
由于没有输入变量,所以这个也能当状态图看
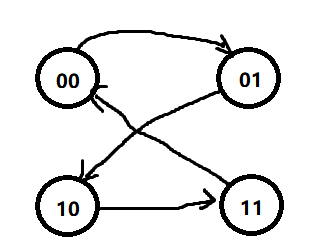
所以这实现了一个四进制的加计数器(00→01→10→11→00)
所谓下边沿就是只有在时钟信号由1转0的瞬间才会改变电路状态
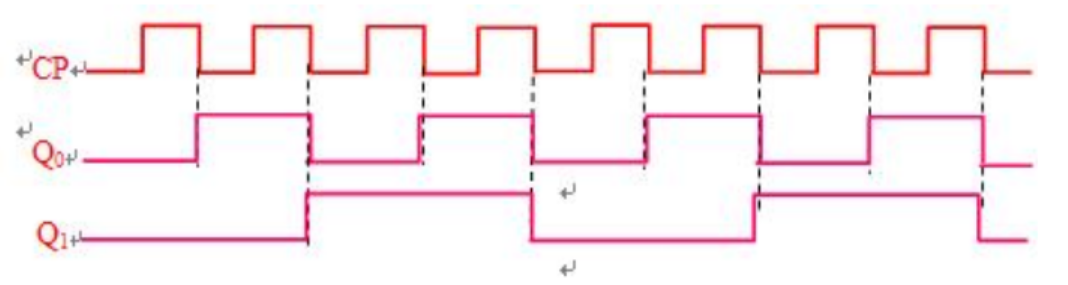
电路设计
电路设计跟分析刚好反过来的
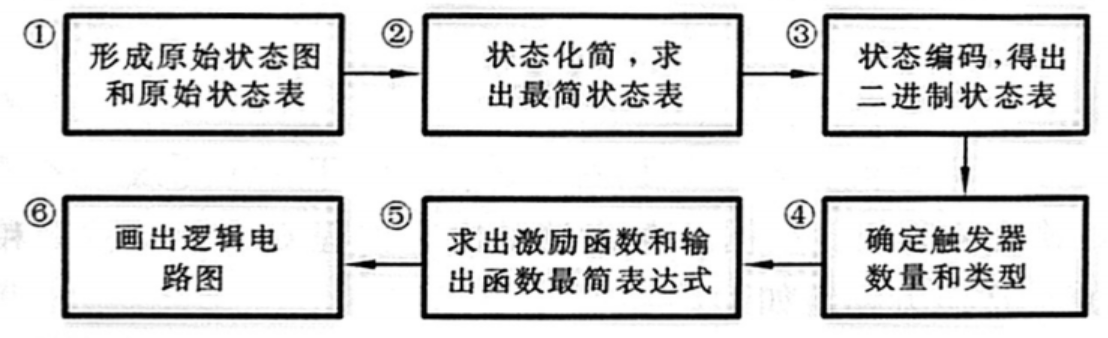
要注意以下几个点:
- 状态表要化到最简,才能知道触发器到底要存几个状态
- 根据存几个状态确定要多少个触发器(比如4个状态就是2个,6个状态就是3个,因为 6 < 2 3 6<2^3 6<23 )
【例】用 J-K 触发器作为存储元件, 设计一个 “ 101 ” 序列检测器。该电路有一个输人
x
\mathrm{x}
x 和一个输出
Z
Z
Z, 当随机输人信号中出现 “101 ”序列时, 输出一个 1 信号。典型输人/输出序列如下。
输入
x
0
0
1
0
1
0
1
1
0
1
0
0
输出
Z
0
0
0
0
1
0
1
0
0
1
0
0
\begin{array}{lllllllllllll} \text { 输入 } \mathrm{x} & 0 & 0 & 1 & 0 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 0 \\ \text { 输出 } \mathrm{Z} & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 1 & 0 & 0 \end{array}
输入 x 输出 Z000010001100111000110000
【解】首先要确定触发器要存几个状态:假设第一个是A状态,输入0没反应,输入1就到了B,B状态要存1,C状态存10,D状态要存“101”同时输出1,这样看来一共要存4个状态,也就是两个触发器。接下来想办法画状态图。这里要借用数据结构与算法中,字符串的模式匹配KMP算法的思想(书本211页)

在A状态下,如果输入1则匹配成功,进入B,如果不成功,则保持A状态

在B状态下,如果输入1则匹配不成功,理应要回A,但1又是A匹配成功的情况,所以保持B状态(这就是改进思想),
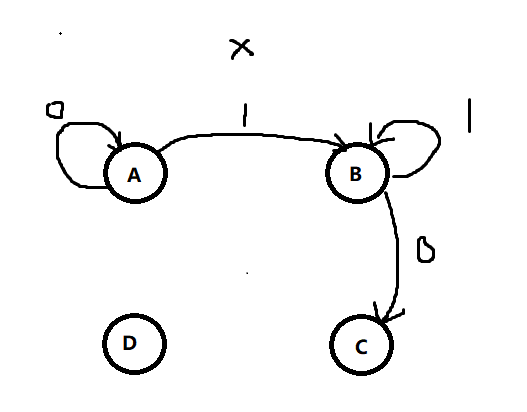
在C状态下,输入1则匹配成功,否则回到A状态
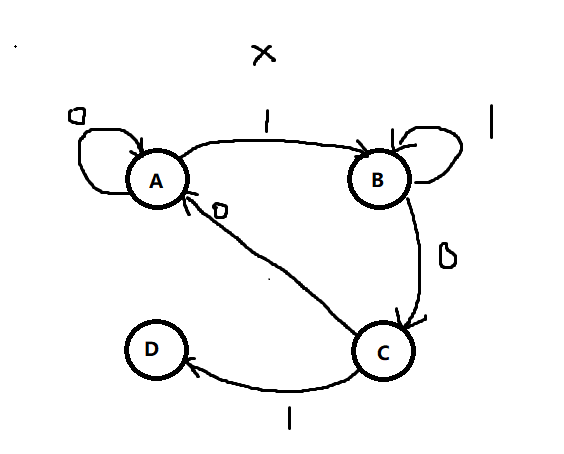
在D状态下,输出一个1,如果再输入1,理应要回A,但1又是A匹配成功的情况,所以直接跳B状态,否则回到A
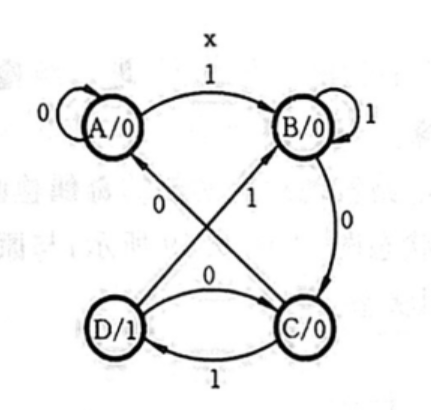
于是得到了状态图,接着我们要用状态图来写二进制真值表,首先要确定一个编码方案,这个就随便写了(因为目前没有理想的公式能概括)
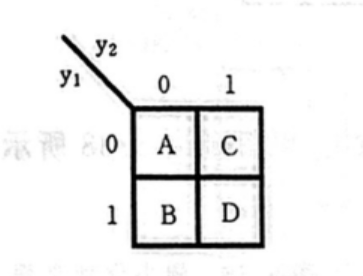
对着编码方案和状态图,就可以写二进制真值表
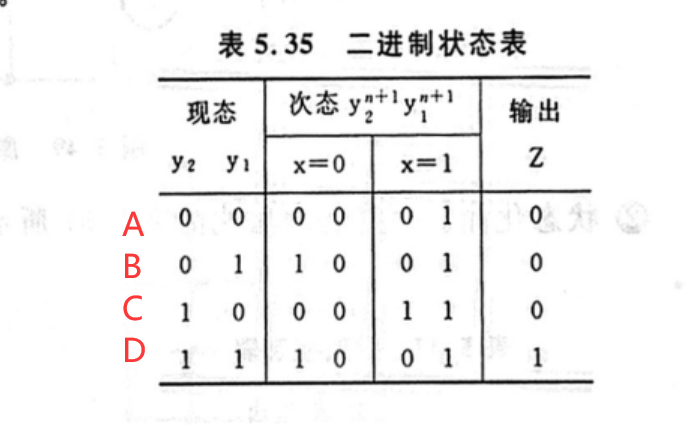
然后确定我们到底用什么触发器,看个人选择了,这里选择J-K触发器,下面是触发器的状态表
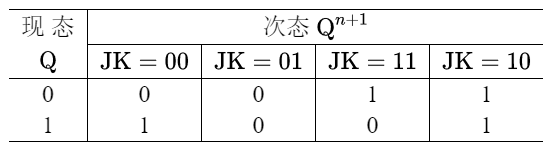
对着触发器的状态表就能对着写次态真值表
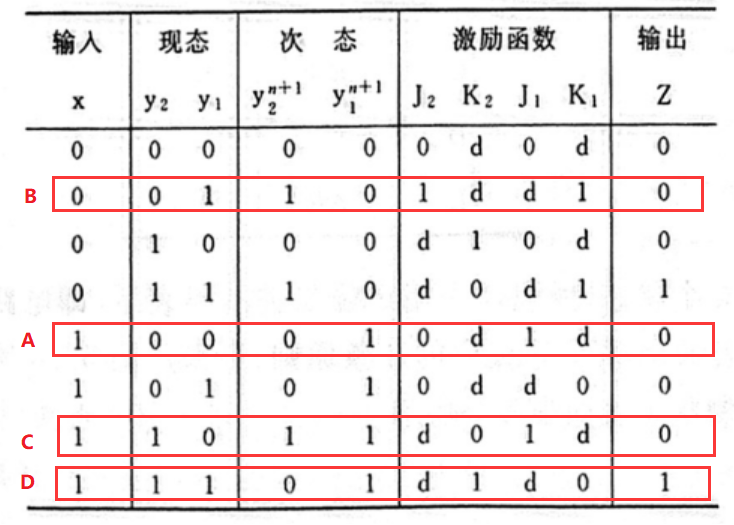
这里举个例子,以A状态为例,考察第一个触发器 y 1 \mathrm{y_1} y1 由于他从0变1 有两种情况,要么是 J K = 11 \mathrm{JK=11} JK=11 要么是 J K = 10 \mathrm{JK=10} JK=10 所以不能确定到底是什么,所以填"d"
为了要确定到底画什么样的电路图,就要确定 J , K \mathrm{J,K} J,K 的函数怎么写,所以要全部列出来,在激励函数中“d”的取值既然可以任意,那就想要什么就要什么,反过来说,就是不考虑“d”的取值,只考虑确定的情况
-
确定 J 1 \mathrm{J_1} J1:先不看“d”,把其他的都看一看 ,你会发现 J 1 \mathrm{J_1} J1 居然可以全部等于输入 x \mathrm{x} x 于是可以得到
J 1 = x \mathrm{J_1 = x} J1=x -
确定 K 1 \mathrm{K _1} K1:先不看“d”,把其他的都看一看 ,你会发现 K 1 \mathrm{K_1} K1 居然全部跟输入 x \mathrm{x} x 相反,于是可以得到
K 1 = x ˉ \mathrm{K_1 = \bar{x}} K1=xˉ -
确定 J 2 \mathrm{J_2} J2:先不看“d”,把其他的都看一看 ,发现除了 x = 0 , y 1 = 1 \mathrm{x=0,y_1=1} x=0,y1=1 的情况下, J 2 = 1 \mathrm{J_2=1} J2=1 以外,其他均为0,于是可以得到
J 2 = x ˉ y 1 \mathrm{J_2=\bar{x}y_1} J2=xˉy1 -
确定 K 2 \mathrm{K_2} K2:先不看“d”,把其他的都看一看 ,同 J 2 \mathrm{J_2} J2 ,可以得到
K 2 = x ˉ y 1 ˉ + x y 1 ˉ = x ˉ ⊕ y 1 \mathrm{K_2=\bar{x}\bar{y_1}+x\bar{y_1}=\bar{x}\oplus y_1} K2=xˉy1ˉ+xy1ˉ=xˉ⊕y1 -
确定 Z \mathrm{Z} Z:这里是输出,所以要关注 y 1 , y 2 \mathrm{y_1,y_2} y1,y2 同理可以得到
Z = y 1 y 2 \mathrm{Z=y_1y_2} Z=y1y2
至此我们可以知道如何画电路图了:对于输入 x \mathrm{x} x 加个非门,两条线分别导触发器(1),触发器(1)引条线跟加过非门的 x \mathrm{x} x 到触发器(2)的 J \mathrm{J} J 线,同时再引条线跟加过非门的 x \mathrm{x} x 组个异或门到触发器(2)的 K \mathrm{K} K 线,最后对两个触发器的输出接一个与门到输出
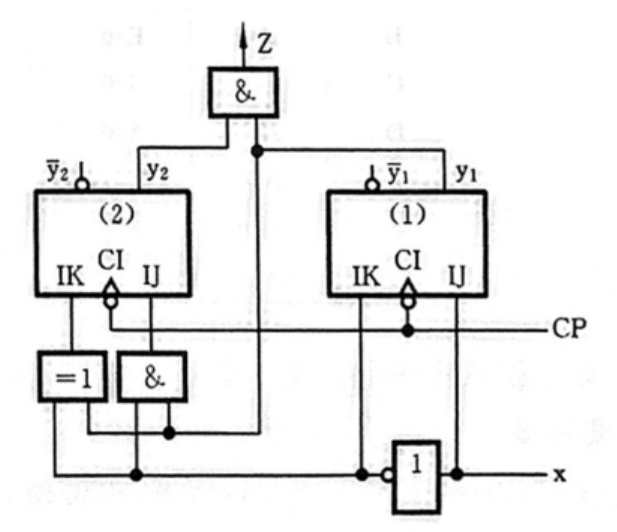
第六章 异步时序逻辑电路
大纲:
- 电路的分析(只考分析不考设计)
异步时序逻辑电路的工作特点是:电路中没有统一的时钟脉冲信号同步,电路状态的改变是外部输入信号变化直接作用的结果;在状态转移过程中,各存储元件的状态变化不一定发生在同一时刻,不同状态的维持时间不一定相同,并且可能出现非稳定状态
根据电路结构模型和输入信号形式的不同,异步时序逻辑电路可分为脉冲异步时序逻辑电路和电平异步时序逻辑电路
脉冲异步时序逻辑电路
脉冲异步时序逻辑电路的存储电路由触发器组成(可以是时钟控制触发器或者非时钟控制触发器),电路输入信号为脉冲信号。
在异步时序逻辑电路中,脉冲信号通常是指一种具有特定持续时间和幅度的短暂信号。这种信号通常由一个快速的上升边缘(也称为正边缘或前沿)和一个稍慢的下降边缘(也称为负边缘或后沿)组成。
电路分析
跟同步时序逻辑是相同的:
- 写出电路的输出函数和激励函数表达式;
- 列出电路次态真值表或次态方程组;
- 作出状态表和状态图;
- 画出时间图并用文字描述电路的逻辑功能。
要注意以下几个点:
- 因为异步时序逻辑电路没有统一的时钟脉冲信号同步,所以触发器的时钟控制端也要当激励函数处理(具体体现在画真值表的时候要考虑时钟控制端 C \mathrm{C} C )
- 不允许出现两个及以上的脉冲,换句话说就是不用考虑这么多情况,假设有3个输入 x 1 , x 2 , x 3 \mathrm{x_1,x_2,x_3} x1,x2,x3 则只需要考虑 001 , 010 , 100 001,010,100 001,010,100 三种情况,其他都不用考虑
【例】分析该电路
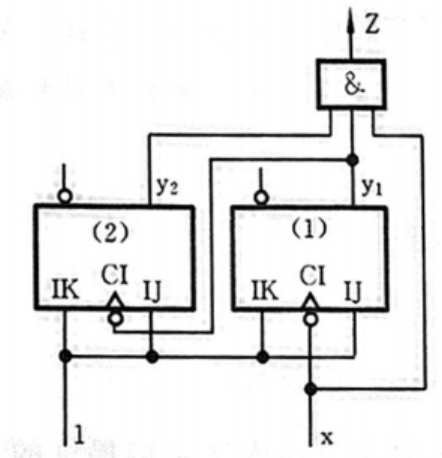
【解】粗略看一下电路大概长这样
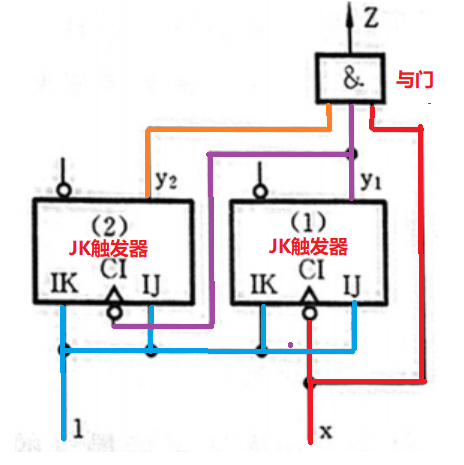
根据这个可以写出激励函数表达式
Z
=
x
y
2
y
1
J
2
=
K
2
=
1
C
2
=
y
1
J
1
=
K
1
=
1
C
1
=
x
\begin{array}{ll} \mathrm{Z}=\mathrm{xy}_2 \mathrm{y}_1 & \\ \mathrm{~J}_2=\mathrm{K}_2=1 & \mathrm{C}_2=\mathrm{y}_1 \\ \mathrm{~J}_1=\mathrm{K}_1=1 & \mathrm{C}_1=\mathrm{x} \end{array}
Z=xy2y1 J2=K2=1 J1=K1=1C2=y1C1=x
接着我们来写次态真值表,前面说过,我们要考虑到时钟信号,因为在触发器中,当信号(
C
P
\mathrm{CP}
CP) 为0时,触发器保持原状态不变。因此我们不需要考虑输入
x
=
0
\mathrm{x=0}
x=0 的情况
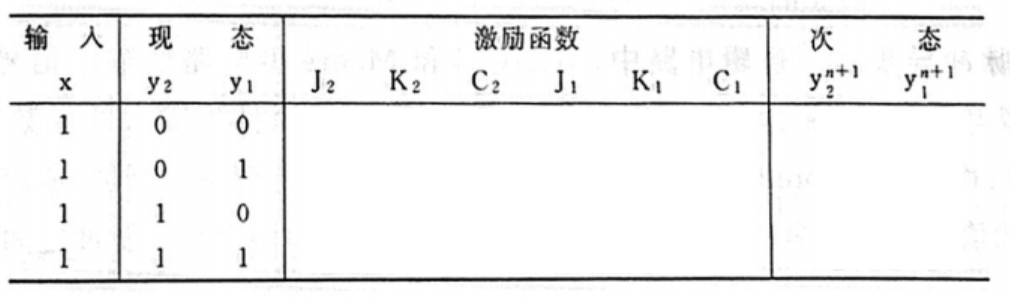
接着来填写激励函数,要注意的是,因为 C 2 = y 1 \mathrm{C}_2=\mathrm{y}_1 C2=y1 会出现触发器(2)不通电的情况,所以 C 2 \mathrm{C_2} C2 可以留空,而 C 1 \mathrm{C_1} C1 需要填一个向下箭头的符号,因为在图中可以知道,该触发器是一个下降沿触发方式
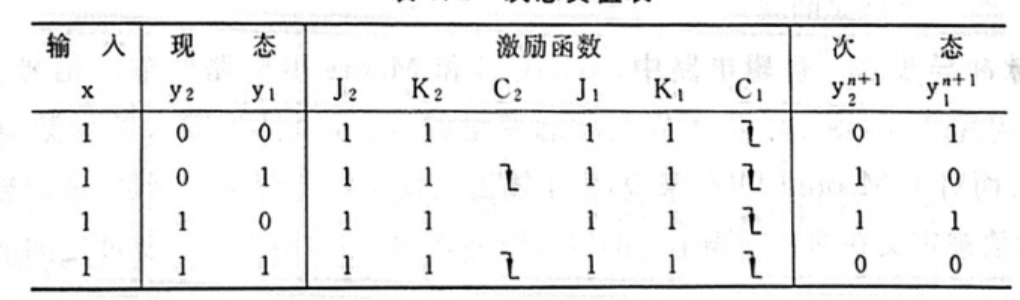
状态表就写出来了
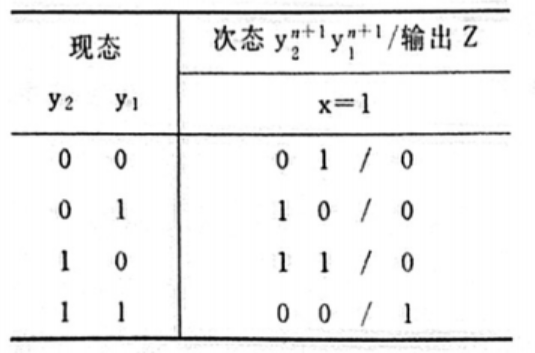
状态图也能画出来
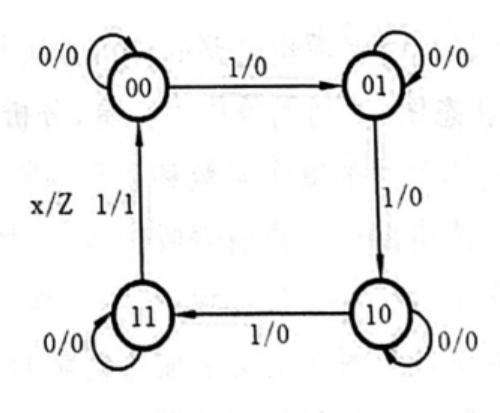
对于时间图,有一些要注意的地方:输入 x \mathrm{x} x 是你自己定的,怎么喜欢怎么来,但为了画图方便,你可以把脉冲间隔画长一点,毕竟脉冲短了就没地方画了
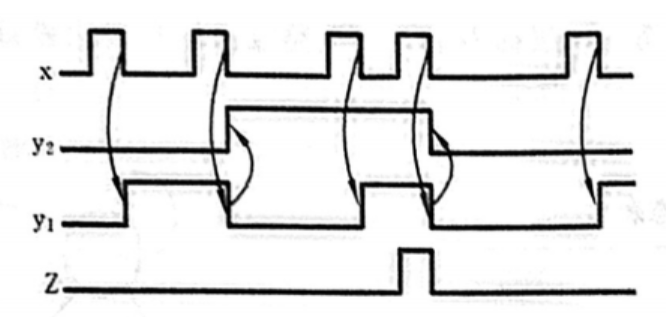
要注意画出时钟信号和对齐触发时间
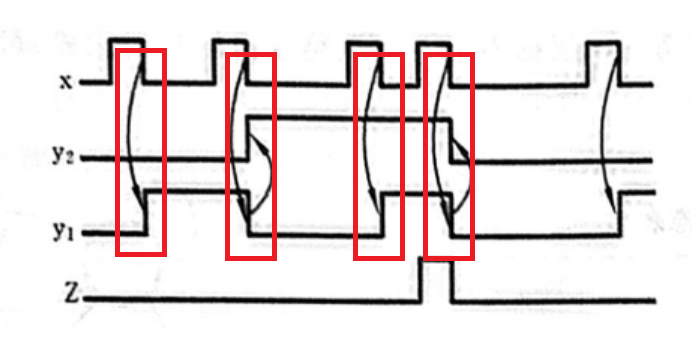
这里的触发器是下降沿触发,所以在脉冲下降沿的时候指一个箭头到触发器(1),同样的触发器(1)的下降沿要引起触发器(2)的变化
电平异步时序逻辑电路
所谓电平信号,其实指的是持续时间不规律的脉冲
这是脉冲信号
这是电平信号

电平异步时序逻辑电路一般长这样
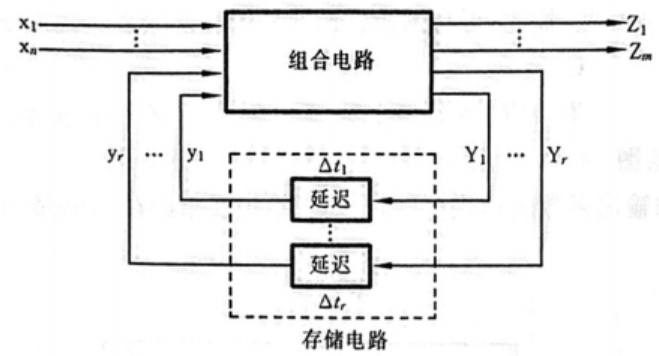
可以看到,存储电路由延迟元件组成(可能是专用的延迟元件或者利用电路本身固有的延迟),终于不用触发器啦🤩
电平异步时序逻辑电路对输入信号有一定要求:
-
不允许两个及以上信号同时变化,这个跟脉冲时序逻辑是一样的
-
必须等内部变化结束变稳定状态(下称稳态)时才允许输入信号发生变化,不然才刚变一半被你打断了,那这个电路就爆了

由于没有了触发器,所以描述方法从真值表变成了流程表,从状态图变成了总态图
流程表:

在流程表中需要对稳态进行特别标注,其实就是给他画个圈圈
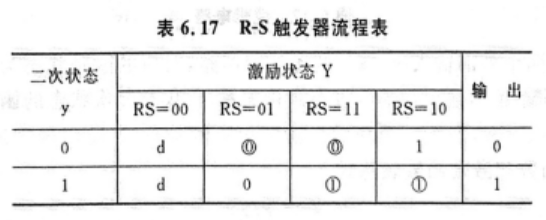
怎么读这个流程表呢,
- 假设RS=10,状态为0,这时候从读表可知下一状态为1,于是就垂直往下跳到稳态
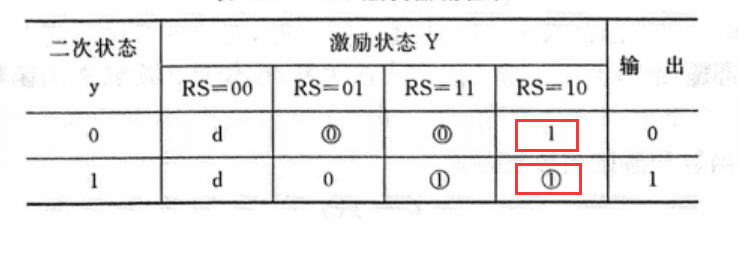
-
假设RS=11,状态为0,如果要从该总态到下一总态,方法是令RS=10
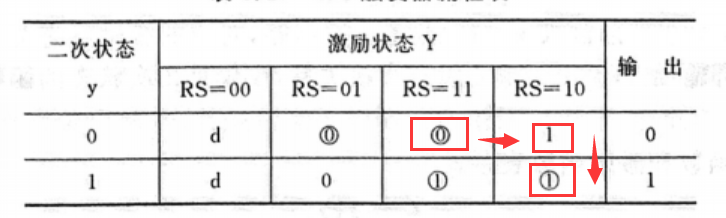
于是可以得出结论:稳态和稳态之间只能通过水平再垂直跳转,也就是说,不是所有的稳态之间都能转换,详细见下面的总态图
总态图:
总态的表达方式是”(输入变量X,激励状态Y)/输出Z“,以上面的R-S触发器为例,他的总态图长这样
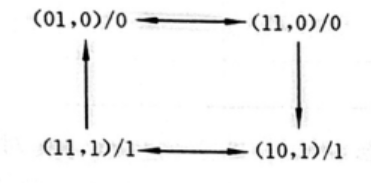
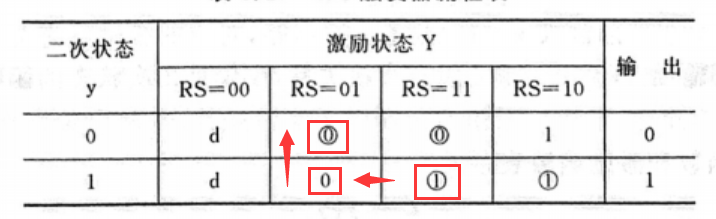
不同总态之间不一定是双向通的,比如(01,0)/0 与 (11,1)/1 在流程图中,可以找到一条线路从 (11,1)/1 到 (01,0)/0 但找不到一条路能从 (01,0)/0到 (11,1)/1
电路分析
电平异步时序逻辑电路的分析过程如下:
- 写出输出函数和激励函数表达式
- 作流程表
- 画总态图或时间图
- 说明功能
【例】分析电路
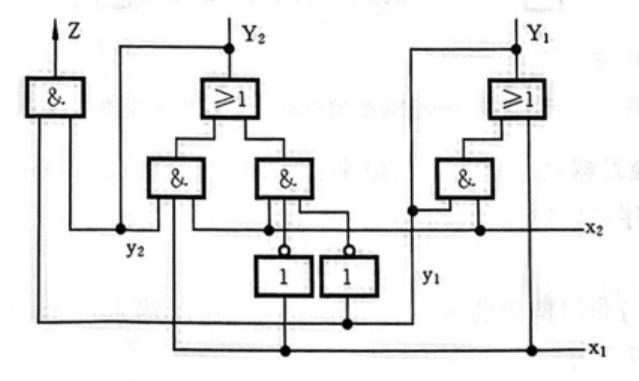
【解】粗略看一眼该电路
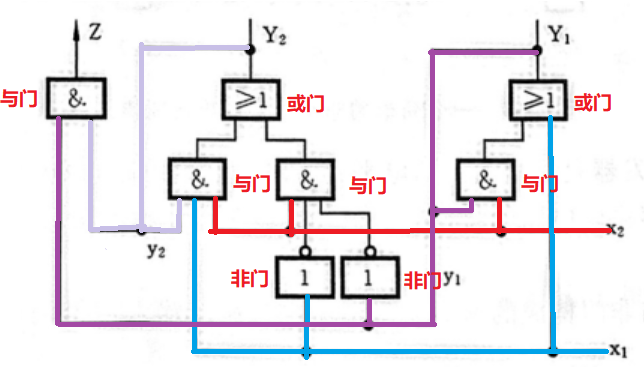
可以写出输出函数和激励表达式
Z
=
y
2
y
1
Y
2
=
x
2
x
1
y
2
+
x
2
x
ˉ
1
y
ˉ
1
Y
1
=
x
2
y
1
+
x
1
\begin{aligned} & \mathrm{Z=y_2y_1}\\ & \mathrm{Y_2=x_2 x_1 y_2+x_2 \bar{x}_1 \bar{y}_1} \\ & \mathrm{Y_1=x_2 y_1+x_1} \end{aligned}
Z=y2y1Y2=x2x1y2+x2xˉ1yˉ1Y1=x2y1+x1
可以作流程表,方式是二次状态和输入按照格雷码的顺序排列,因为不允许一下子变两个
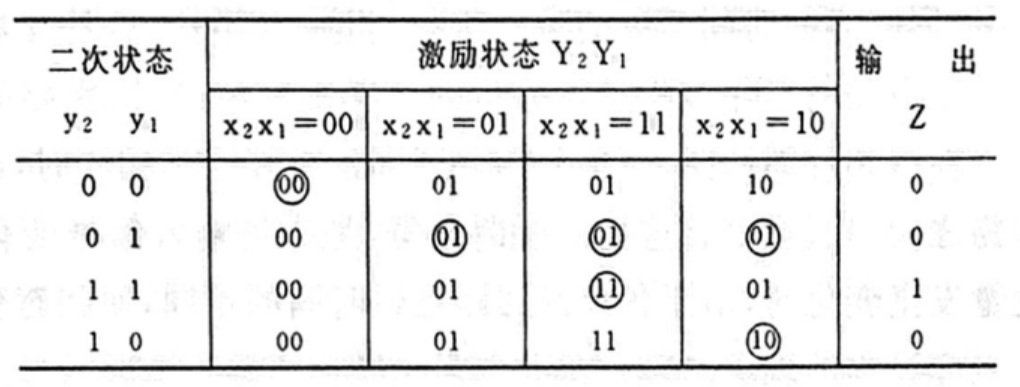
总态图就出来了
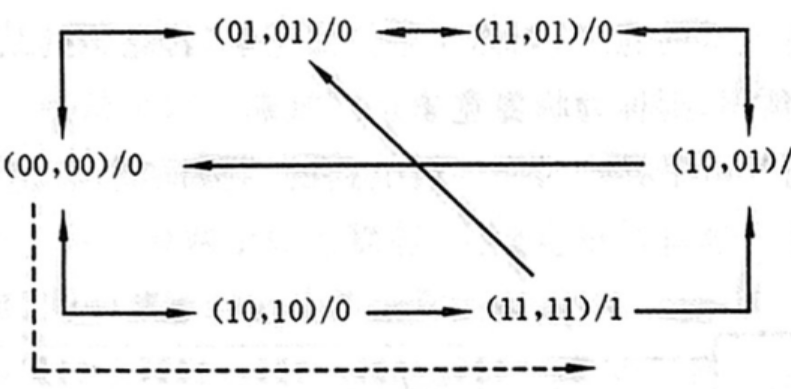
其实在这里就能看出来到底在干什么了,你可以从输出“1”这里开始看,然后反过来推
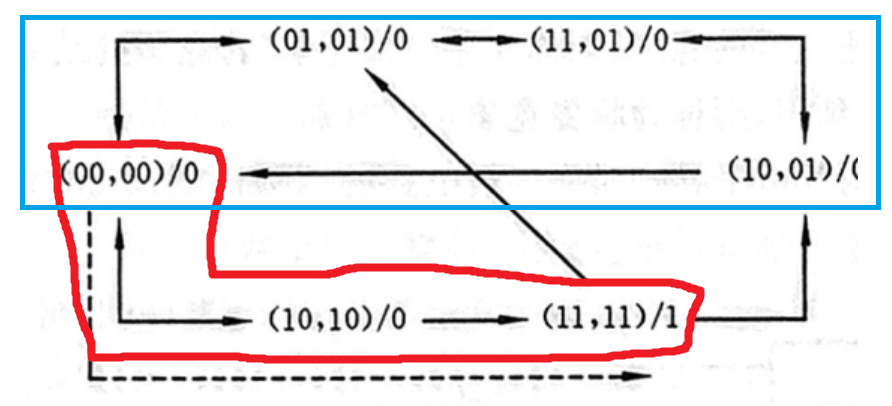
蓝色框是一个大循环,来回转换,这种一般没有什么意义,可以看到红色部分,一旦从00 到了 10 再到11 就能输出一个1,说明这是一个“00→10→11”序列检测器
这时候就有疑问了,凭什么是“00→10→11” 我说“01→00→10→11” 和“10→11” 不行吗? 这就涉及到"最小公因数"的思想了,这个问题可以转化成:
判断句子中是否有“吃饭”这个词
1)今天我去吃饭了→有
2)昨天我没有吃饭→有
3)后天会有人送饭→无
在这个例子中,显然不能用“去吃饭了”来判断到底有没有“吃饭”,因为这样第二个就判断不出来了,同样也不能以“饭”来判断,不然第三个就是了。因此这个序列一定要保证足够简短的同时又有效,回到刚才的例子中,只有“(00,00)/0”条件下才有可能走通到输出“1”,而(01,01)/0 和“(10,01)/0” 都能走,故他们不能作为判断序列
为了例题的完整性,给出时间图的画法,首先要写出相应序列

然后你要凸显这个时间延迟 也就是说你要画出中间过渡态(打*号的地方),然后你要等过渡完了才能输入下一个状态
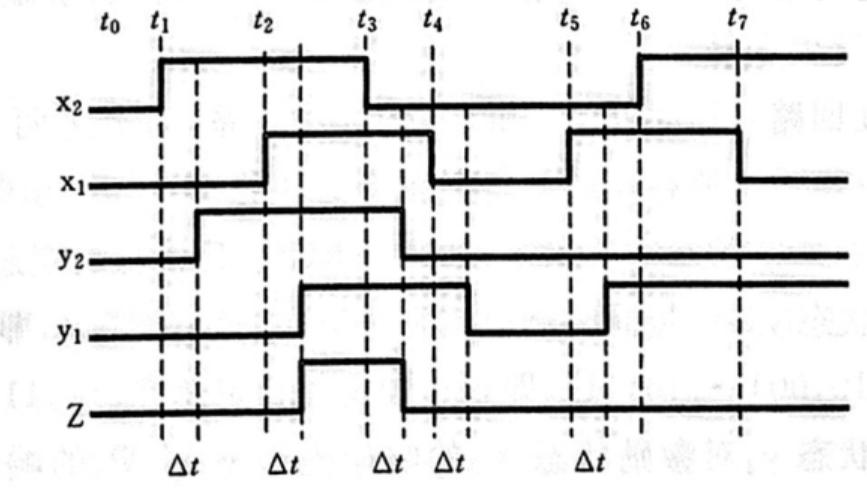
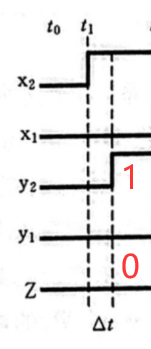
下面我们来解读这个时间图,为了凸显这个时间延迟,我们假设跳两次总态的时间为 Δ t \Delta t Δt ,为什么是两次呢 ,因为从一个总态到另一个总态刚好只能跳两次,详见总态的介绍。
从 t 0 t_0 t0 到 t 1 t_1 t1 ,即输入从 00 00 00 到 10 10 10 ,要发生 ( 00 , 00 ) → ( 10 , 00 ) → ( 10 , 10 ) (00,00)→(10,00)→(10,10) (00,00)→(10,00)→(10,10) 的变化,所以在变化的瞬间, y 2 , y 1 y_2,y_1 y2,y1 不会立即变化,而是在 $\Delta t $ 的时间段后从 00 → 10 00→10 00→10
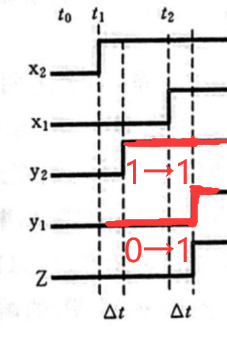
从 t 1 t_1 t1 到 t 2 t_2 t2 ,即输入从 10 10 10 到 11 11 11 ,要发生 ( 10 , 10 ) → ( 11 , 10 ) → ( 11 , 11 ) (10,10)→(11,10)→(11,11) (10,10)→(11,10)→(11,11) 的变化,所以在变化的瞬间, y 2 , y 1 y_2,y_1 y2,y1 不会立即变化,而是在 $\Delta t $ 的时间段后从 10 → 11 10→11 10→11





















 786
786











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








