写在前面的
这本书的作者是Dimitri Panteli Bertsekas教授,1942年出生于希腊雅典,美国工程院院士,麻省理工大学电子工程及计算机科学教授。Bertsekas教授因其在算法优化与控制方面以及应用概率论方面编写了多达16本专著而闻名于世。他也是CiteSeer搜索引擎学术数据库中被引用率最高的100位计算机科学作者之一。Bertsekas教授还是Athena Scientific出版社的联合创始人。
我们知道,动态规划和最优化控制可以解决大型的多阶段决策问题,本书关注的重点是在计算资源有限的情况下,如何获得获得近似解。并且要求找到的近似解达到一定的性能需求。而这类方法通常被统称为强化学习,有时也会被叫做近似动态规划或神经动态规划。
本书的主要灵感来自于最优化控制领域和人工智能领域的结合。本文的主要目之一就是探索这两个领域之间的边界,并为这两个领域的工作人员搭建互联互通的桥梁。
本书的相关资源:
官网 REINFORCEMENT LEARNING AND OPTIMAL CONTROL :BOOKS, VIDEOLECTURES, AND COURSE MATERIAL
这本书的官方网站有对应的PDF(只不过是草稿,只有前四章的内容,建议直接买书,不过目前只有英文版的),还有相关的课件和视频(需翻墙)。
不过作者也在B站发布了上课的视频:
在知乎上也有大佬分享他的学习笔记:
这位大佬是control的背景,对optimal control和经典的数学优化的各种programming比较熟悉,而本人最近开始学习这本书,之前有一些强化学习的基础,在做机器人的一些应用,觉得这本书挺有价值,所以在此记录一下学习的过程,督促自己自学,也希望和大家一起讨论学习。
本篇文章对应书中的 1.1. Deterministic Dynamic Programming 和 1.2. Stochastic Dynamic Programming.
确定性动态规划(Deterministic Dynamic Programming)
所有的动态规划(以下简称为DP,Dynamic Programming)问题都包括一个离散时间的动态系统,其具有以下形式:
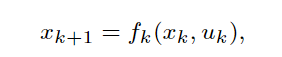
其中是时间索引,
是系统的状态,
是控制或决策变量,在时间
从集合
中选择,这是因为
一般会具有某种约束,比如机器人在地图中可以上下左右地走,但最上方的时候无法选择向上的动作,
是描述系统动态特性的一个关于(
)的函数,
是表示这个系统有
个时间步,这里先讨论
是有限的情况。
这类问题还包含一个cost function的情况,也就是我们需要考虑成本,比如寻路问题中要求总的路径和最小,燃料问题中使用的燃料要少等等。在本书中用表示在时间
中花费的成本。很容易就知道,这种成本是随着时间增加的,所以在初始状态为
,控制序列为
{
}的总花销为:

其中是在终止状态下花费的成本。
在整个系统中,我们的目的当然就是在每个状态中选择的
的总花费最小,也就是
最小,其中最优的符号一般用星号(*)表示:

所以DP问题可以用下图描述:

动态规划算法
最优原则(Principle of Optimality)
动态规划算法其实就是将待求解的问题分解为若干个子问题,按顺序求解子阶段,前一子问题的解,为后一子问题的求解提供了有用的信息。下面具体说一下:
定义{}为最优的控制序列,所以在初始状态
之后对应的状态都是最优的状态,即{
}。我们考虑中间的一步,即在时间为
之后的情况:

显然这是原问题的一个子问题,这个子问题的最优解就是{} 。
最优原则就是说原问题的最优解的一个子序列({}就是从{
}中拿出来的),就是子问题的最优解。注意这个子问题得是最终状态相同,就是所有子问题开头可以不一样,但是结尾必须和原问题一样,这种子问题英文上叫做Tail subproblem,如下图所示:

文中有个例子比较直白,就是假设洛杉矶到芝加哥的最短路径会经过波士顿,那么波士顿到芝加哥的最短路径也会经过这里。
动态规划寻找最优控制序列
通过上面的学习我们可以知道求解原问题的最优解可以分解成求解不同的Tail subproblem的最优解:

其中:
![]()

也就是说,是从
到
的一个最小的花费,从式子可以看到,如果我们要计算
,每次都要算从
到
的总花销,为此用了一种归纳(Induction)的方法:

这样只要我们算好,只要加上
就可以得出
,其实在强化学习中也用到了这个思想,
是立即的花费,而
代表未来的花费,叫做cost-to-go funtion。
在得到了之后,我们就可以利用这些funtion来求解最优控制序列了,其实就是找到一个
,使得
最小:

值空间近似
由上面的学习我们也知道,要求解一个最优序列我们需要计算,这需要考虑所有的
和
,就是这一部分:
![]() ,这很花计算的时间。为此采用了一种近似的方法,将
,这很花计算的时间。为此采用了一种近似的方法,将
替换成,这个近似有很多种方式,例如我们知道神经网络可以拟合函数,那么这个
可以用神经网络来表示,直接输入
和
就能直接输出结果,不需要考虑所有的
和
。

本书用Q-factors来表示上图式子(1.9)的右半部分:

即:

这个近似的Q-factors也可以用神经网络等方法来实现,然后在强化学习的方法中求解Q-factors的方法就叫做Q-learning。
相对于近似的,自然就有最优的
,我们的目的就是使得它们越相近越好,这个后面再说,由上面式子自然得出:

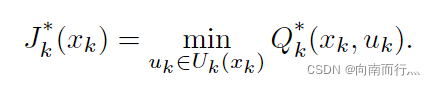
它也有归纳的形式,推导其实都很简单,可以私下推导加强理解:

随机动态规划(Stochastic Dynamic Programming)
其实随机性问题相比于确定性问题只是多了一个干扰的随机变量,
服从于一个概率的分布
。这种系统的表示形式如下:
![]()
其它的一些定义如图所示:

和确定性问题有一个比较重要的区别是我们要优化的不再是控制序列{},而是策略(policies):
![]()
其中,是状态
到控制
的映射
,并且满足控制的约束。策略比控制序列更通用,在存在随机不确定性的情况下,它们可以降低成本,因为它们根据
(这通常包含一些知识)选择
。如果没有这些知识,控制器就不能适应某些意外状况(因为有个随机变量
),从而对成本造成不利影响。这是确定性和随机最优控制问题之间的一个根本区别。
还有一个区别就是用了期望来表示,这也是因为存在了随机变量
,一般用Monte Carlo simulation获得:

其它部分就和确定性问题的差别就不是很大了,我就放一部分方便对比:
DP求解随机性问题:

随机性问题中的Q-Factors,可以看出只是多了一个随机变量 :



写在后面的
下一章地址:


























 1940
1940

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










