双目视觉三维重建之求两异面直线公垂线中点坐标的解法

前言

双目立体视觉系统三维重建原理如图所示，对于每个相机而言，如果光心和像点已知，就可以确定光心和像点组成的唯一射线。在针孔成像模型下，物点必然在此射线上。由两台相机进行交汇就有两条这样的射线，且所有的射线都应经过物点，即采用各射线在物点相交这一原理，就可以对空间物点进行交汇定位。同理，在存在折射平面的情况下，可以通过四元数等手段确定交互的射线的方向向量和射线通过的已知点(如折射平面上的点)。由于图像平面坐标的测量误差、噪声以及相机畸变等因素的影响, 两条射线可能不会相交, 所以交汇定位问题就是求异面直线公垂线段中点的坐标。

三维重建原理

已知：

空间中两异面直线的单位方向向量分别为：

且两条直线分别过点,：

假设：

作两条异面直线的公垂线，设公垂线与两直线的交点（垂足）分别为：

1.解法一

解法一参考文献原图

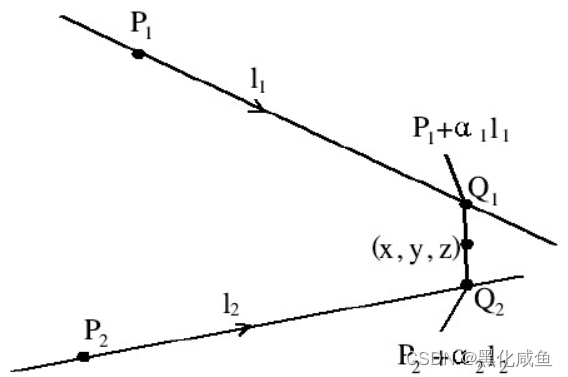
设两条直线上存在滑动的两个点分别为，则两点坐标的参数形式（直线参数方程）为：

由异面直线公垂线的定义可知：

即当Q点与M点重合时，Q点坐标即为中垂线的垂足坐标。 

由公垂线与两直线垂直，向量内积为0得：

联立方程解得参数的值：

进一步可解出垂足坐标，从而得到中垂线的中点坐标

2.解法二

解法二参考文献原图

由直线方向向量可求中垂线的方向向量：

由空间几何关系可知直线的方向向量、中垂线的方向向量、直线上某点到垂足的向量在同一平面上,即点构成一个平面，构成另一个平面，则有：

由上式可解出垂足坐标，从而得到中垂线的中点坐标

3. 解法三

先求公垂线的方向向量：

进一步确定左右相机射线分别与公垂线确定的两个平面：

其中，右相机射线与公垂线确定的平面过点，且法向量为： 

则该平面的平面方程为：

同理，左相机射线与公垂线确定的平面过点，且法向量为：

则该平面的平面方程为：

接下来只需求直线与平面的交点，可得到公垂线的垂足。

求左相机射线与平面的交点： 

解得：

求右相机射线与平面的交点：

 

解得：

代入参数方程可得公垂线与两条射线的交点，即垂足。易得公垂线的中点。 

参考文献

[1]罗世民,李茂西.双目视觉测量中三维坐标的求取方法研究[J].计算机工程与设计,2006(19):3622-3624.DOI:10.16208/j.issn1000-7024.2006.19.037.

[2]马峰,李琼砚,赵亚东.异面直线公垂线段中点算法为基的三维点重建[J].现代制造工程,2009(07):98-102.DOI:10.16731/j.cnki.1671-3133.2009.07.033.