Expected Calibration Error (ECE)模型校准原理解析

Expected Calibration Error (ECE)模型校准原理解析

 对于高风险应用来说，机器学习模型对其预测的置信度是至关重要的。model calibration（模型校准）就是要让模型结果预测概率和真实的经验概率保持一致。模型校准这个话题比较小众，博主也是在看一篇Self-KD的论文时才看到的。模型校准的metrics有很多，这里博主仅仅讨论Expected Calibration Error (ECE)这一个比较经典的模型校准metric。

参考资料

• Measuring Calibration in Deep Learning，有公式
• 叫我如何相信你？聊一聊语言模型的校准
• On Calibration of Modern Neural Networks

1. 什么是模型校准？

 模型校准就是要让模型结果预测概率和真实的经验概率保持一致。说人话也就是，在一个二分类任务中取出大量（M个）模型预测概率为0.6的样本，其中有0.6M个样本真实的标签是1。总结一下，就是模型在预测的时候说某一个样本的概率为0.6，这个样本就真的有0.6的概率是标签为1。

 上面是一个正面的例子，下面我再来举一个反面的例子说明模型校准的重要性。还是在一个二分类任务中取出大量（M个）模型预测概率为0.6的样本，而这些样本的真实标签全部都是1。虽然从accuracy的角度来考察，模型预测样本概率为0.6最后输出时会被赋予的标签就是1，即accuracy是100%。但是从置信度的角度来考察，这个模型明显不够自信，本来这些全部都是标签为1的样本，我们肯定希望这个模型自信一点，输出预测概率的时候也是1。

2. Expected Calibration Error (ECE)

 有了前面对模型置信度的感性了解，我们接下来看看该怎么用Expected Calibration Error去定量度量。首先来一张原论文On Calibration of Modern Neural Networks的图：

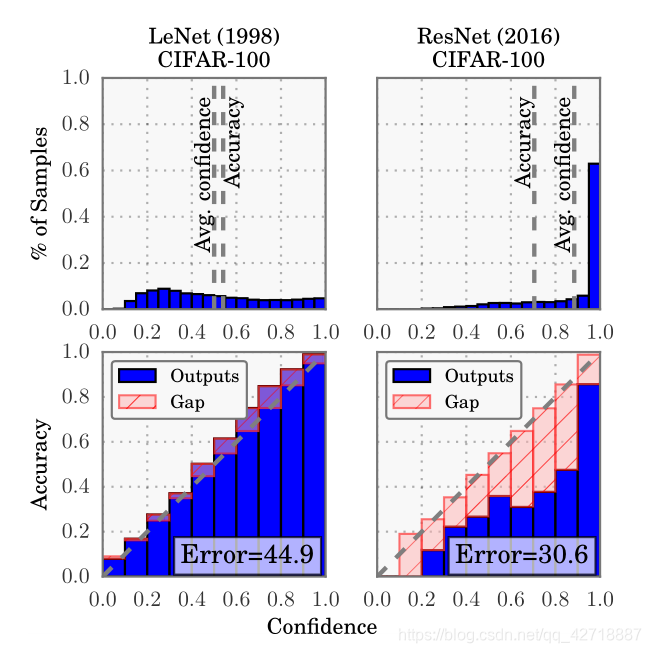
 为了能够定量地度量置信度，作者将[0, 1]区间划分为多个bin（这里划分为了5个bin），所有的二分类样本都将根据模型对其预测的结果分别落入这5个bin之中的1个。在每个bin之中计算平均的模型confidence，再与该bin中样本真实标签的平均accuracy进行对比，两者之差的绝对值就能度量模型的置信度，差距越大代表模型置信度越小。公式如下：
$$ECE=\sum _{b=1}^B\frac{n_b}{N}|acc(b)-conf(b)|\text{\hspace{1em}(1)}$$

 其中，b代表第b个bin，B代表bin的总数，$n_b$代表第b个bin中样本的总数，acc(b)代表第b个bin中样本真实标签的平均值，conf(b)代表第b个bin中模型预测概率的平均值。