卷积神经网络中的平移等变性分析

点击上方“小白学视觉”，选择加"星标"或“置顶”

重磅干货，第一时间送达

卷积神经网络（CNN）具有平移等变性的观点在某种程度上深入人心，但很少有人去探寻其原因或者理论根据。这篇文章将对这个问题进行系统地讲解，为后续进一步研究CNN的其他等变性和不变性设计夯实基础。

介绍

在机器学习中，我们通常关注模型的灵活性。我们希望知道选择的模型实际上能够完成我们想要的任务。例如，神经网络的通用逼近定理使我们相信神经网络可以近似任何所需精度的广泛类别的函数。但完全的灵活性也有缺点。虽然我们知道我们可以学习目标函数，但也存在许多错误的函数，它们在我们的训练数据上看起来完全一样。如果我们是完全灵活的，我们的模型可能会学习其中任何一个函数，一旦我们移开了训练数据，我们可能无法进行泛化。因此，需要对网络的灵活性加以限制。卷积神经网络是减少灵活性的一个著名成功案例。相较于早期的MLP网络，CNN的卷积牺牲了一部分灵活性，但实现了图像数据的平移等变性，这对于图像处理是十分重要的性质。

什么是平移等变性映射

简而言之，等变性映射是保留变换的代数结构的映射。作为一个特殊情况，平移等变映射是一种映射，当输入被平移时，会导致一个映射发生相应的平移，如下图所示：

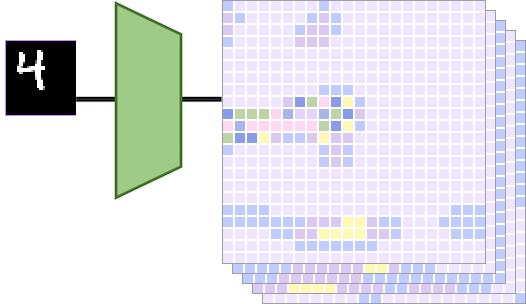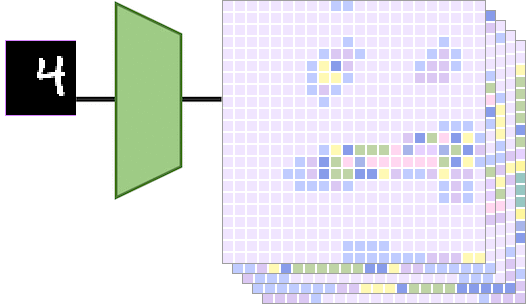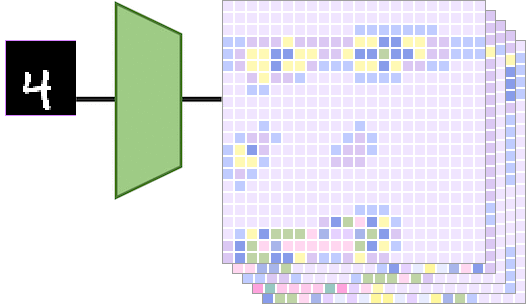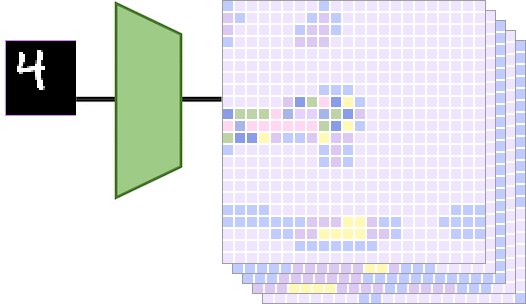
当左边的输入图像被平移一定的量时，输出特征图也会被相同的量进行平移。具体而言，如下图所示，

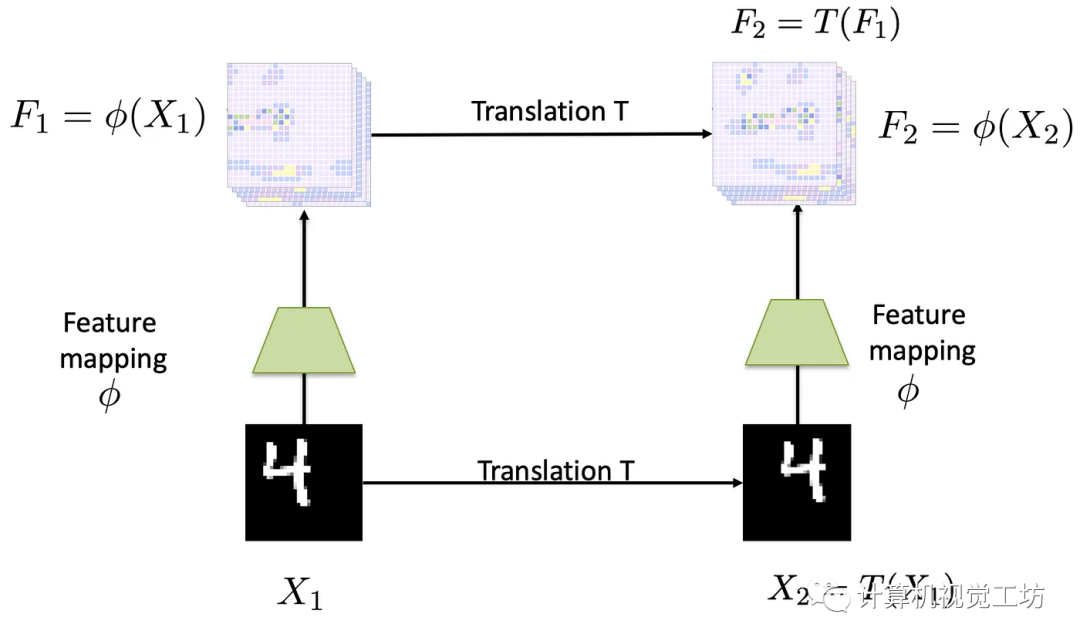
输入图像显示数字“4”，向右平移得到另一个输入图像。和分别是通过平移等变映射计算得出的特征图。在这种情况下，通过将传递给得到的特征图相当于对特征图做相同的平移得到的特征图。

卷积的平移等变性证明

首先让我们写下卷积的定义：

本质上，这定义了一个相关性(Correlation)而不是卷积(Convolution)。然而，在深度学习领域中的惯例是将其称为卷积，这里我们将沿用这个惯例。在这里，和都有个通道。为了简洁，本文中我们取。

现在,我们的目标是，给定一张图像，我们将用滤波器对其进行卷积。然后，我们想验证对于任何平移，以下两个操作是相同的：

• 将平移，然后将结果与进行卷积。

• 将与进行卷积，然后将结果平移。

因此，我们需要证明的方程是：

证明

注意到我们可以通过替换重写卷积：

现在我们来分别写出我们想要证明的等式两边的定义。首先，对于 的定义：

还有 的定义：

这两个表达式是相等的，所以证毕。

思考

值得进一步思考的是，这种等价性为什么成立。我们进行的 的替换之所以有效，有两个原因：

• 这个替换是从到的双射。

• 求和是在整个空间上进行的。

这两个特性加在一起可以确保，在左边求和式中出现的每一项也都会出现在右边的求和式中，反之亦然。

同时，这种推理方法与卷积神经网络中的平移等变性的实际局限性相符，即卷积不是完全的平移等变性。这是因为总会在边界上丢失信息，换句话说，在实际应用中，并不是对整个求和，而只对其一个子集求和。这违反了上面的第二点，因此替换并不完全成立，导致了卷积的平移等变性的局限性。

下载1：OpenCV-Contrib扩展模块中文版教程

在「小白学视觉」公众号后台回复：扩展模块中文教程，即可下载全网第一份OpenCV扩展模块教程中文版，涵盖扩展模块安装、SFM算法、立体视觉、目标跟踪、生物视觉、超分辨率处理等二十多章内容。


下载2：Python视觉实战项目52讲
在「小白学视觉」公众号后台回复：Python视觉实战项目，即可下载包括图像分割、口罩检测、车道线检测、车辆计数、添加眼线、车牌识别、字符识别、情绪检测、文本内容提取、面部识别等31个视觉实战项目，助力快速学校计算机视觉。


下载3：OpenCV实战项目20讲
在「小白学视觉」公众号后台回复：OpenCV实战项目20讲，即可下载含有20个基于OpenCV实现20个实战项目，实现OpenCV学习进阶。


交流群

欢迎加入公众号读者群一起和同行交流，目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群（以后会逐渐细分），请扫描下面微信号加群，备注：”昵称+学校/公司+研究方向“，例如：”张三 + 上海交大 + 视觉SLAM“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~