数学建模理论自制笔记1：微分方程及其模型

最新推荐文章于 2023-07-09 21:16:02 发布

绿镇

最新推荐文章于 2023-07-09 21:16:02 发布

阅读量2k

点赞数 3

分类专栏：数学建模文章标签：数学

本文链接：https://blog.csdn.net/qq_42914565/article/details/124660302

版权

数学建模专栏收录该内容

6 篇文章 1 订阅

订阅专栏

1、微分方程基础概念：

微分方程：含有自变量、未知函数及未知函数的导数或微分的等式，其定义式为 $f\left ( x,y,y',y'',\cdots ,y^{(n)} \right )=0$ ；
常微分方程（Ordinary Differential Equations, ODE）：不含偏导数或偏微分的微分方程，即对于函数 $f$ 来说仅含有一个独立变量 $x$ 的微分方程；
偏微分方程（Partial Differential Equations, PDE）：含有偏导数 $f^{'}_{x}\left ( x_{0},y_{0} \right )=\frac{\partial f}{\partial x}\left ( x_{0},y_{0} \right )$ 或偏微分的微分方程，即对于函数 $f$ 来说包含两个或两个以上的独立变量 $x, y,\cdots$ 的微分方程；
微分方程的阶数：微分方程中所出现的未知函数的导数（或微分）的最高阶数，如有 $n$ 个，就称为 $n$ 阶常/偏微分方程；其中2阶及以上阶数的微分方程称作高阶微分方程；
微分方程的通解：微分方程的解中含有任意变化的常数，且任意变化的常数的个数与微分方程的阶数相同，这样的解称为通解；
常微分方程的初值问题/柯西问题：在给微分方程添加附加条件时，附加条件中未知函数及其导数的独立变量取值相同，比如在 $x=1$ 的情况下，对于常微分方程给出了 $y\left ( 1 \right )$ 和 $y'\left ( 1 \right )$ 的值；
常微分方程的边值问题：在给微分方程添加附加条件时，附加条件中未知函数及其导数的独立变量取值不同，比如在 $x=1$ 的情况下，对于常微分方程给出了 $y\left ( 1 \right )$ 和 $y'\left ( 2 \right )$ 的值；

2、一阶微分方程的常见形式：

标准形式： $y'=f\left ( x,y \right )$ ，大部分一阶微分方程都可以通过代数方法写成该形式；
微分形式： $M\left ( x,y \right )dx+N\left ( x,y \right )dy=0$ ，它和标准形式是等价的且可以相互转化；
变量分离方程： $M\left ( x \right )dx+N\left ( y \right )dy=0$ ；
齐次一阶微分方程： $y'=f\left ( \frac{y}{x} \right )$ ，即满足 $f\left ( tx,ty \right )=f\left ( x,y \right )$ 特性的方程，其中 $f\left ( x,y \right )$ 称为齐次函数；
全微分方程/恰当方程：变量分离方程 $M\left ( x,y \right )dx+N\left ( x,y \right )dy=0$ 里满足 $\frac{\partial M\left ( x,y \right )}{\partial y}=\frac{\partial N\left ( x,y \right )}{\partial x}$ 的方程，此为全微分方程的充要条件；详细的定义是：存在二元函数 $u\left ( x,y \right )$ 满足 $du\left ( x,y \right )=M\left ( x,y \right )dx+N\left ( x,y \right )dy$ ，即 $u\left ( x,y \right )$ 的全微分是 $M\left ( x,y \right )dx+N\left ( x,y \right )dy$ ，满足 $u\left ( x,y \right )$ 为 $M\left ( x,y \right )dx+N\left ( x,y \right )dy$ 的原函数；
一阶线性微分方程： $y'+p\left ( x \right )y=q\left ( x \right )$ ；当 $q\left ( x \right )=0$ 时， $y'+p\left ( x \right )y=0$ 称作一阶齐次线性方程，表示线性方程里常数项为0，当然它在这里也是变量分离方程；
伯努利微分方程： $y'+p\left ( x \right )y=q\left ( x \right )y^{n}$ ；当 $n=0$ 或 $1$ 时，方程会退化为线性方程形式；

3、一阶常微分方程的解法：

变量分离方程 $M\left ( x \right )dx+N\left ( y \right )dy=0$ ：在两端积分变成 $\int M\left ( x \right )dx+\int N\left ( y \right )dy=C$ 即可求解；
齐次一阶微分方程 $y'=f\left ( \frac{y}{x} \right )$ ：令 $\frac{y}{x}=k$ （注：这里 $k$ 不是常数），则可得 $x\frac{dk}{dx}+k=f\left ( k \right )$ ，通过化简可得关于 $x,k$ 的变量分离方程形式，之后在两端积分即可求解；
全微分方程/恰当方程：首先需要验证微分方程为全微分方程，判别方法就是证明成立，根据是否成立分为以下两种情况：
1. $\frac{\partial M\left ( x,y \right )}{\partial y}=\frac{\partial N\left ( x,y \right )}{\partial x}$ 成立：说明 $M\left ( x,y \right )dx+N\left ( x,y \right )dy=0$ 为全微分方程，就需要求出 $M\left ( x,y \right )dx+N\left ( x,y \right )dy$ 的原函数 $u\left ( x,y \right )$ ；已知 $\left\{\begin{matrix} u_{x}=\frac{\partial u}{\partial x}=M\left ( x,y \right )\\ u_{y}=\frac{\partial u}{\partial y}=N\left ( x,y \right ) \end{matrix}\right.$ ，首先对 $\frac{\partial u}{\partial x}=M\left ( x,y \right )$ 两边关于 $x$ 积分，得 $u\left ( x,y \right )=\int M\left ( x,y \right )dx+h\left ( y \right )$ ，再让这个式子两边对 $y$ 求导，得 $\frac{\partial u}{\partial y}=\frac{\partial }{\partial y}\int M\left ( x,y \right )dx+h'\left ( y \right )$ ；将其与 $u_{y}=\frac{\partial u}{\partial y}=N\left ( x,y \right )$ 对应得 $h'\left ( y \right )=N\left ( x,y \right )-\frac{\partial }{\partial y}\int M\left ( x,y \right )dx$ ，然后再在其两边关于 $y$ 积分即可求出 $h\left ( y \right )$ ，最后代入 $u\left ( x,y \right )=\int M\left ( x,y \right )dx+h\left ( y \right )$ 中可求出原函数 $u\left ( x,y \right )$ ；那么 $u\left ( x,y \right )=C$ 就是全微分方程的通解；
2. $\frac{\partial M\left ( x,y \right )}{\partial y}=\frac{\partial N\left ( x,y \right )}{\partial x}$ 不成立：需要引入积分因子 $\mu \left ( x,y \right )$ ，使得非全微分方程 $M\left ( x,y \right )dx+N\left ( x,y \right )dy=0$ 变为全微分方程 $\left (\mu \left ( x,y \right )M\left ( x,y \right ) \right )dx+\left (\mu \left ( x,y \right )N\left ( x,y \right ) \right )dy=0$ ，之后就可以利用上述方法求解；积分因子的求解视 $\frac{1}{N\left ( x,y \right )}\left ( \frac{\partial M\left ( x,y \right )}{\partial y}-\frac{\partial N\left ( x,y \right )}{\partial x} \right )$ 的值或者微分方程形态而定：
  1. 当 $\frac{1}{N}\left ( \frac{\partial M}{\partial y}-\frac{\partial N}{\partial x} \right )\equiv g\left ( x \right )$ 时（即结果仅是 $x$ 的函数）： $\mu \left ( x,y \right )=e^{\int g\left ( x \right )dx}$ ；
  2. 当 $\frac{1}{N}\left ( \frac{\partial M}{\partial y}-\frac{\partial N}{\partial x} \right )\equiv h\left ( y \right )$ 时（即结果仅是 $x$ 的函数）： $\mu \left ( x,y \right )=e^{-\int h\left ( y \right )dy}$ ；
  3. 当 $\left\{\begin{matrix} M=yf\left ( xy \right )\\ N=xg\left ( xy \right ) \end{matrix}\right.$ 时（即 $\frac{M}{y}$ 和 $\frac{N}{x}$ 仅是 $xy$ 的函数）： $\mu \left ( x,y \right )=\frac{1}{xM-yN}=\frac{1}{xy\left ( f\left ( xy \right )-g\left ( xy \right ) \right )}$ ；
  4. 当不满足以上三种情况时，建议采用其他方法求解；
伯努利微分方程 $y'+p\left ( x \right )y=q\left ( x \right )y^{n}$ ：令 $z=y^{1-n}$ ，即可将方程转换为一阶线性常微分方程形式，再按照上面1-3里对应方程的求解方法求出 $z$ 的通解，之后利用 $z=y^{1-n}$ 求 $y$ 的通解；

4、可降阶高阶微分方程的求解：

$y^{(n)}=f(x)$ 型微分方程（ $n$ 阶微分方程）：对该 $n$ 阶微分方程两边进行 $n$ 次积分，即可得到该方程的通解；
$y''=f\left ( x,y' \right )$ 型微分方程（不含 $y$ ）：令 $y'=p(x)$ ，则 $y''=p'(x)$ ，即可将原来的方程化为 $p'=f(x,p)$ ，很明显这就是一阶微分方程的标准形式，利用上述知识找出对应一阶常微分方程的形式求解；之后利用 $y'=p(x)$ 两边积分，求解 $y=\int p(x)dx+C$ 得原方程的通解；
$y''=f(y,y')$ 型微分方程（不含 $x$ ）： 将 $y$ 视作自变量，令 $y'=p(y)$ ，那么 $y''=p'(x)=\frac{dp}{dx}=\frac{dp}{dy}\frac{dy}{dx}=p\frac{dp}{dy}$ ，即可将原来的方程化为 $p\frac{dp}{dy}=f\left ( y,p \right )$ ，很明显这也近似于一阶微分方程的标准形式，利用上述知识找出对应一阶常微分方程的形式求解；

5、微分方程的模型：

按已知规律建模法：在物理、化学等学科中，许多现象所符合的规律或定律都已知道，建模时只需要依据这些规律，给出一些变量与变化率之间的关系，即可列出微分方程。使用这种方法时，首先要确立实际问题中的几个要素，例如自变量、未知函数、必要的参数与常数、坐标系等；然后找到一些与未知函数的变化率有关的规律及定律；最后按照已知的规律列出微分方程；
微元分析法：根据某些已知的规律及定律直接建立变量的微元之间的关系式，即可建立微分方程。使用这种方法时，首先要确立实际问题中的几个变量，再建立这些变量的微元，最后按照这些微元之间的关系列出等式，加以整理即可得到微分方程；
近似待定模拟校正法：在生物、经济等学科提出的一些实际问题中，一些现象的规律还不十分清楚，而且是极其复杂的，要用数学模型去研究这些实际问题，只能用近似待定模拟校正法。具体而言，是要作出各种假设，在不同的假设下去建立近似的模型。然后从数学上求解由这样近似所建立的微分方程或者分析解的性质，再与实际现象对比，看这个微分方程模型能否刻画、模拟、近似某些实际现象，如果不行，再进一步修订校正，直到合理为止。

6、微分方程建模的步骤：

把用语言描述的情况转化为文字方程；
陈述出所涉及的原则或定律；
建立微分方程;；
确定约束条件；
求出微分方程的通解；
求出微分方程通解中的任意常数；
给出问题答案；
检验答案是否满足问题的要求。

7、微分方程建模模型举例：

饿狼追兔问题：现有一只兔子，一匹狼，兔子位于狼的正西100米处。假设兔子与狼同时发现对方并一起起跑，兔子往正北60米处的巢穴跑，而狼在追兔子，已知兔子、狼是匀速跑且狼的速度是兔子的两倍。问题是兔子能否安全回到巢穴？
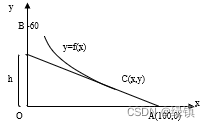
- 首先建立如图所示的坐标系，设兔子在 $O$ 处，狼在 $A$ 处。由于狼要盯着兔子追，所以狼行走的是一条曲线，且在同一时刻，曲线上狼的位置与兔子的位置的连线为曲线上该点处的切线。设狼的行走轨迹是 $y=f\left ( x \right )$ ，则有 $f(100)=0,f'(100)=0$ ，假设在某一时刻，兔子跑到 $D\left ( 0,h \right )$ 处，而狼在 $C\left ( x,y \right )$ 处，则有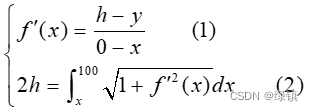，整理得到下述式子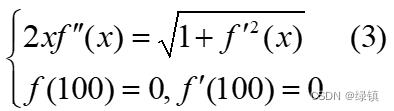：，很明显这属于 $y''=f\left ( x,y' \right )$ 型微分方程，即可降阶的二阶微分方程，解得狼的行走轨迹为 $f(x)=\frac{1}{30}x^{\frac{3}{2}}-10x^{\frac{1}{2}}+\frac{200}{3}$ ；而因为 $f(0)=\frac{200}{3}>60$ ，所以狼追不上兔子。
尸体冷却问题：某地发生一起凶案，受害者的尸体于晚上7:30在其家中被发现，法医于晚上8:20赶到凶案现场，测得尸体温度为32.6℃；一小时后，当尸体即将被抬走时，测得尸体温度为31.4℃，室温在几个小时内始终保持21.1℃。此案最大的嫌疑人张某某声称自己是无罪的，并有证人说：“下午张某某一直在办公室上班，5:00时打完电话后就离开了办公室”。从嫌疑人张某某到受害者家（凶案现场）步行需5分钟，现在的问题是，嫌疑人张某某不在凶案现场的证言能否被采信，使他排除在嫌疑之外。
- 首先应确定凶案的发生时间，若死亡时间在下午5:05之前，则张某某就可以排除嫌疑，否则不能排除；
- 设 $f(t)$ 表示 $t$ 时刻尸体的温度，单位为摄氏度，并记晚上8:20为 $t=0$ ，则 $f(0)=32.6,f(1)=31.4$ 。假设受害者死亡时体温是正常的，即 $f=37$ 对应的时间是受害者死亡的时间，也就是求 $f(t)=37$ 的时刻 $t$ ，进而确定张某某是否是嫌疑犯;
- 人体体温受大脑神经中枢调节。人死亡后体温调节的功能消失，尸体的温度受外界环境温度的影响。假设尸体温度的变化服从牛顿冷却定律，即尸体温度的变化率与他同周围的温度差成正比。即： $\frac{df}{dt}=-k\left ( f-21.1 \right )$ ，解答这个变量分离方程得 $f(t)=21.1+ae^{-kt}$ ，带入 $f(0),f(1)$ ，解得 $f(t)=21.1+11.5e^{-0.11t}$ ，当 $f=37$ 时，有 $t=-2.95$ （2h57min)，8h20min－2h57min＝5h23min。即死亡时间大约在下午5:23，因此张某某不在凶案现场的证言不能被采信，不能被排除在嫌疑之外。
马尔萨斯（Malthus）人口模型/指数增长模型：在人口自然增长过程中，净相对增长（出生率与死亡率之差）是常数，即单位时间内人口的增长量与人口成正比，比例系数设为 $r$ ，在此假设下，推导并求解人口随时间的变化；
- 设时刻 $t$ 的人口为 $N(t)$ , 把 $N(t)$ 当作连续、可微函数处理，据马尔萨斯的假设，在 $t$ 到 $t+\Delta t$ 时问段内，人口的增长量为 $N(t+\Delta t)-N(t)=rN(t)\Delta t$ ，即有 $\frac{dN}{dt}=rN$
- 设 $t=t_{0}$ 时刻的人口为 $N_0$ ，于是有 $N(t_0)=N_0$ ， $\left\{\begin{matrix} \frac{dN}{dt}=rN\\N(t_0)=N_0 \end{matrix}\right.$ 这个联立式就是马尔萨斯人口模型，求解这个变量分离方程可得 $N(t)=N_0 e^{r\left ( t-t_0 \right )}$ ，此式表明人口以指数规律随时间无限增长；
- 马尔萨斯模型的一个显著特点是：种群数量翻一番所需的时间是固定的。令种群数量翻一番所需的时间为 $T$ ，则有： $2N_0=N_0e^{rT}$ ，那么 $T=\frac{\ln 2}{r}$ ；
- 模型检验：据估计1961年地球上的人口总数为 $3.06\times 10^9$ ，而在以后7年中，人口总数以每年2%的速度增长，即 $t_0=1961,N_0=3.06\times 10^9,r=0.02$ ；于是 $N(t)=3.06\times 10^9e^{0.02\left ( t-1961 \right )}$ ；比较历年的人口统计资料，可发现人口增长的实际情况与马尔萨斯模型的预报结果基本相符，例如，1961年世界人口数为30.6亿（即 $3.06\times 10^9$ ），人口增长率约为2%，人口数大约每35年增加一倍。检查1700年至1961的260年人口实际数量，发现两者几乎完全一致，且按马尔萨斯模型计算，人口数量每34.6年增加一倍，两者也几乎相同；
- 模型预测：假如人口数真能保持每34.6年增加一倍，那么人口数将以几何级数的方式增长。例如，到2510年，人口数将达到 $2\times10^{14}$ 个，即使海洋全部变成陆地，每人也只有9.3平方英尺的活动范围，而到2670年，人口数将达到 $3.6\times 10^{16}$ 个，只好一个人站在另一人的肩上排成二层了。故马尔萨斯模型是不完善的。

Logistic模型/阻滞增长模型：马尔萨斯模型为什么不能预测未来的人口数呢？这主要是地球上的各种资源只能供一定数量的人生活，随着人口的增加，自然资源环境条件等囚素对人口增长的限制作佣越来越显著，如果当人口较少时，人口的自然增长率可以看作常数的话，那么当人口增加到一定数量以后，这个增长率就要随人口的增加而减小；因此应对马尔萨斯模型中关于净增长率为常数的假设进行修改。
- 1838年，荷兰生物数学家韦尔侯斯特（Verhulst）引入常数 $N_m$ （最大人口容量），用来表示自然环境条件所能容许的最大人口数，并假设增长率等于 $r\left ( 1-\frac{N(t)}{N_m} \right )$ ，即净增长率随着 $N(t)$ 的增加而减小，则当 $N(t)\rightarrow N_m$ 时，净增长率趋于0，按此假定建立人口预测模型；
- 由韦尔侯斯特假定，马尔萨斯模型应改为即Logistic模型，该变量分离方程的解为；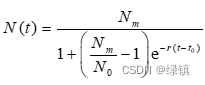
- 模型检验：用该模型检验美国从1790年到1950年的人口数，发现模型计算的结果与实际人口数在1930年以前都非常吻合，自从1930年以后，误差愈来愈大，一个明显的原因是在20世纪60年代美国的实际人口数已经突破了20世纪初所设的极限人口数。由此可见该模型的缺点之一是 $N_m$ 不易确定。事实上，随着一个国家经济的腾飞，它所拥有的食物就越丰富， $N_m$ 的值也就越大；
- 模型预测：用Logistic模型来预测世界未来人口总数。某生物学家估计， $r=0.029$ ，又当人口总数为 $N=3.06\times 10^9$ 时，人口每年以2%的速率增长。由Logistic模型得： $\frac{1}{N}\frac{dN}{dt}=r\left ( 1-\frac{N}{N_m} \right )$ ；解得 $N_m=9.86\times 10^9$ ，即世界人口总数极限值约为100亿。

参考资料：

微分方程(1)-基本概念及分类 - 知乎 (zhihu.com)
微分方程第五节可降阶的高阶微分方程 - 知乎 (zhihu.com)

绿镇

关注

3
点赞
踩
32

收藏

觉得还不错? 一键收藏
0
评论
数学建模理论自制笔记1：微分方程及其模型

1、微分方程基础概念：微分方程：含有自变量、未知函数及未知函数的导数或微分的等式，其定义式为；常微分方程（Ordinary Differential Equations, ODE）：不含偏导数或偏微分的微分方程，即对于函数来说仅含有一个独立变量的微分方程；偏微分方程（Partial Differential Equations, PDE）：含有偏导数或偏微分的微分方程，即对于函数来说包含两个或两个以上的独立变量的微分方程；微分方程的阶数：微分方程中所出现的未知函数的导数（或微分）的最高阶数，
复制链接

扫一扫