详解利用均匀随机分布的变量生成服从高斯分布的变量

问题可以阐述如下：

有一个$[-1,1]$均匀分布的随机变量作为输入$x$，编写一个函数使之输出为一个均值为$0$，方差为$1$，服从高斯分布的变量。（公式推导和程序实现）

已知高斯分布的概率密度函数：
$$p(x)=\frac{1}{\sqrt{2\pi }\sigma }\exp \left\{-\frac{1}{2}(\frac{x-\mu }{\sigma }{)}^2\right\}\text{\hspace{1em}(1)}$$
根据题干要求，分布中的参数分别为：$\mu =0,{\sigma }^2=1$，即标准高斯分布：
$$p(x)=\frac{1}{\sqrt{2\pi }}\exp \left(-\frac{x^2}{2}\right)\text{\hspace{1em}(2)}$$
根据二维正态分布下，若两个分量独立，则其模服从瑞利分布，即可通过标准的分布函数求反函数的方法实现：利用[0,1]的均匀随机分布数列得到服从高斯分布的变量。

令$I={\int }_{-\infty }^{\infty }{e}^{-\frac{x^2}{2}}dx$，则
$$I^2={\int }_{-\infty }^{\infty }{e}^{\frac{-x^2}{2}}dx{\int }_{-\infty }^{\infty }{e}^{\frac{-y^2}{2}}dy={\int }_{-\infty }^{\infty }{e}^{-\frac{x^2+y^2}{2}}dxdy\text{\hspace{1em}(3)}$$
用三角函数来对上式进行表示，即令$x=r\cos \theta ,y=r\sin \theta$
$$I^2={\int }_0^{2\pi }{\int }_0^{\infty }{e}^{-\frac{r^2}{2}}rdrd\theta =2\pi {\int }_0^{\infty }{e}^{-\frac{r^2}{2}}rdr=2\pi \text{\hspace{1em}(4)}$$
将$(X,Y)$作为相互独立的标准正态分布变量，对应的联合概率密度函数$f_{(X,Y)}(x,y)$可表示为：
$$\begin{array}{rl}{f}_{(X,Y)}(x,y)& =f(x)\times f(y)\\ & =\frac{1}{\sqrt{2\pi }}\exp \left(-\frac{x^2}{2}\right)\frac{1}{\sqrt{2\pi }}\exp \left(-\frac{y^2}{2}\right)\\ & =\frac{1}{2\pi }{e}^{-\frac{x^2+y^2}{2}}\end{array}\text{\hspace{1em}(5)}$$
令$x=R\cos \theta ,y=R\sin \theta$，使得两个正态分布变量可以通过向量$\text{r}$来表示（包含大小$R$和角度$\theta$两个分量），由于$\theta$在$[0,2\pi ]$的区间内均匀采样，则这个二维正态分布关于R的分布函数可表示为:
$$P(R\le r)={\int }_0^{2\pi }{\int }_0^r\frac{1}{2\pi }{e}^{\frac{-u^2}{2}}udud\theta ={\int }_0^r{e}^{\frac{-u^2}{2}}udu=1-e^{\frac{-r^2}{2}}\text{\hspace{1em}(6)}$$
其中$X,Y\sim N(0,{\sigma }^2),R^2=X^2+Y^2$，$R$表示向量$X,Y$的模，$R$的分布函数$F_R(r)$则可表示为：
$$F_R(r)=1-e^{\frac{-r^2}{2}}\text{\hspace{1em}(7)}$$
其中$Z$表示在取值为$R$处所对应的瑞利分布函数（$R$的分布函数）$F_R(r)$，且根据Eq(7)可知二维正态分布概率密度函数中的$e^{\frac{-r^2}{2}}$服从指数分布，即半径大小$r$在二维平面中所对应的分布也为指数分布。

因此，由于服从指数分布，因此可以直接对这一分布进行逆变换采样，生成结果为$[0,1]$区间上均匀分布的随机变量，因此通过对Eq(7)求反可得：
$$R=F_R^{-1}(Z)=\sqrt{-2\ln (1-Z)}\text{\hspace{1em}(8)}$$
综上，整个推导过程可以理解为：将二维正态分布的概率密度函数（probability density function，PDF）以向量形式看做两个独立部分的乘积，即Eq(9)中蓝色和红色两部分：
$$\begin{array}{rl}{f}_{(X,Y)}(x,y)& =f(x)\times f(y)\\ & =\frac{1}{2\pi }{e}^{-\frac{x^2+y^2}{2}}\end{array}\text{\hspace{1em}(9)}$$

1. 第一部分为$[0,2\pi ]$范围中的均匀分布，代表了二维平面向量中的角度$\theta$；
2. 第二部分则表现为$\lambda =1$的指数分布，对应了向量模的大小。

因此，可以通过两个服从$[0,1]$均匀分布的样布转化为所对应的角度和半径，其方法如下：

1. 模部分：根据Eq(8)中的逆变换结果，生成$[0,1]$的均匀分布，对应了二维平面向量中的模
2. 角度：生成$[0,1]$之间的均匀分布，乘以参数$2\pi$，即为二维平面向量所对应的角度。

对应的输入形式如下，假设有服从$[0,1]$均匀分布的随机变量$U_1,U_2$，对应参数可描述为：
$$\begin{array}{rl}& Z=U_1\\ & \theta =2\pi U_2\end{array}\text{\hspace{1em}(10)}$$
将Eq(10)带入到$x=R\cos \theta ,y=R\sin \theta$中，对应结果为：
$$\begin{array}{rl}X& =R\cos (\theta )=\sqrt{-2\ln (1-U_1)}\cos (2\pi U_2)\\ Y& =R\sin (\theta )=\sqrt{-2\ln (1-U_1)}\sin (2\pi U_2)\end{array}\text{\hspace{1em}(11)}$$
其中$X,Y$均为一个均值为$0$，方差为$1$，服从高斯分布的变量。
注：由于题目中的输入的均匀分布随机变量U1范围为[-1,1]，只需要对变量进行(U1+1)./2的变化即可变换为一个均值为0，方差为1，服从高斯分布的变量

下面给出程序实现：

function [normdistribution] = uniform2norm(U1)
	U1 = (U1+1) ./ 2;
	U2=rand(1,length(U1));
	X=sqrt(-2 * log(1-U1)) .* cos(2*pi .* U2);
	Y=sqrt(-2 * log(1-U1)) .* sin(2*pi .* U2);
	normdistribution=[X,Y];
	histogram(normdistribution,100);

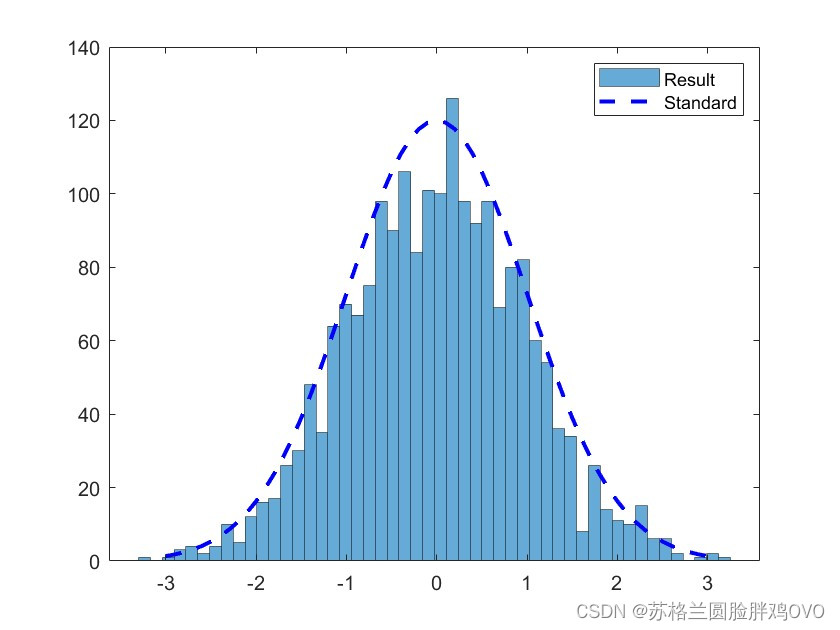
结果如下：