利用qiskit实现量子门以及态的初始化

最新推荐文章于 2024-09-12 09:28:36 发布

keep_humble

最新推荐文章于 2024-09-12 09:28:36 发布

阅读量5.5k

点赞数 4

分类专栏：量子编程文章标签：量子门量子态保真度

本文链接：https://blog.csdn.net/qq_43270444/article/details/120676931

版权

量子编程专栏收录该内容

16 篇文章

订阅专栏

前言

在开始正题之前，先提供一下基础知识。

量子密码学习笔记-量子态与量子门_keep_humble的博客-CSDN博客https://blog.csdn.net/qq_43270444/article/details/108664850

写在前面：最开始单比特门我都是利用u1,u2,u3函数实现的，但是今天又跑了一下，提示现在用的是u（），所以我就把之前的代码调了一下，可能会有遗漏的地方，请见谅~

1.单比特门

1.1 General-U Gates

单比特量子特可以表示为：

对于任意的单比特量子态，我们可以通过酉门实现一个量子态到另一个量子态的转换。

我们将General-U门分为U3,U2,U1：

当θ=π/2，U2门：

当θ=0，Φ=0, U1门:

下面是General-U gates的实现，我们需要注意的地方是U3,U2,U1所含参数的数目

# Useful additional packages
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
from math import pi
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, execute
from qiskit.tools.visualization import circuit_drawer
from qiskit.quantum_info import state_fidelity
from qiskit import BasicAer
# 实现一个单元格有多个输出，不要忘记！！！
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = 'all'
# 指定用什么模拟器，除此之外还有qasm_simulator,statevector_simulator
backend = BasicAer.get_backend('unitary_simulator')
 
#方式1：先创建寄存器，再添加到量子电路
#创建两qubits的量子寄存器，命名为q1
q0 = QuantumRegister(2,'q1')
#创建两bits的经典寄存器，命名为c1
c0 = ClassicalRegister(2,'c1')
 
#创建量子电路
circuit = QuantumCircuit(q0,c0)
 
 
#为qubit1添加U3门，U3（）包含四个参数，前三个参数为θ，Φ和λ值，最后一个参数为作用的qubit
circuit.u(pi/2,pi/2,pi/2,0)
 
#为qubit2添加U2门，U2（）包含三个参数，前两个参数为Φ和λ值，最后一个参数为作用的qubit
circuit.u(pi/2,pi/2,pi/2,1)
 
#为qubit2添加U1门，U1（）包含两个参数，前一个参数为λ值，最后一个参数为作用的qubit
circuit.u(0,0,pi/4,1)
 
 
#电路可视化，以mpl形式输出，会自动调节输出电路的大小
circuit.draw(output='mpl')

1.2 Pauli门、H、S、T 等单比特门

# 导入包
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
from math import pi
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, execute
from qiskit.tools.visualization import circuit_drawer
from qiskit.quantum_info import state_fidelity
from qiskit import BasicAer

# 实现一个单元格有多个输出，不要忘记！！！
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = 'all'

# 指定用什么模拟器，除此之外还有qasm_simulator,statevector_simulator
backend = BasicAer.get_backend('unitary_simulator')

#创建两qubits的量子寄存器，命名为q1
q0 = QuantumRegister(2,'q1')
#创建两bits的经典寄存器，命名为c1
c0 = ClassicalRegister(2,'c1')

#创建量子电路
circuit = QuantumCircuit(q0,c0)

#添加量子门
circuit.i(0)
circuit.h(0)

# Pauli-X,Y,Z
circuit.x(1)
circuit.y(1)
circuit.z(1)

#S,T,S+,T+
circuit.s(1)
circuit.t(1)
circuit.sdg(1)
circuit.tdg(1)

#旋转门
#qubit1绕x轴旋转π/2
circuit.rx(pi/2,0)
#qubit2绕y轴旋转π/2
circuit.ry(pi/2,1)
#qubit1绕z轴旋转π/4
circuit.rz(pi/4,0)

#测量
circuit.measure_all()

#电路可视化，以mpl形式输出，会自动调节输出电路的大小
circuit.draw(output='mpl')

2.两比特门

2.1 swap门、受控门

# 导入包
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
from math import pi
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, execute
from qiskit.tools.visualization import circuit_drawer
from qiskit.quantum_info import state_fidelity
from qiskit import BasicAer
# 实现一个单元格有多个输出，不要忘记！！！
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = 'all'
# 指定用什么模拟器，除此之外还有qasm_simulator,statevector_simulator
backend = BasicAer.get_backend('unitary_simulator')
 
#方式1：先创建寄存器，再添加到量子电路
#创建两qubits的量子寄存器，命名为q1
q0 = QuantumRegister(2,'q1')
#创建两bits的经典寄存器，命名为c1
c0 = ClassicalRegister(2,'c1')
 
#创建量子电路
circuit = QuantumCircuit(q0,c0)
circuit.swap(0,1)
 
#添加control-H门，qubit1：控制位；qubit2：目标位
circuit.ch(0,1)
 
# control-X,Y,Z
circuit.cx(0,1)
circuit.cy(0,1)
circuit.cz(0,1)
 
#control-Rx,y,z
circuit.crz(pi/2,0,1)
circuit.crx(pi/4,1,0)
circuit.cry(pi/2,1,0)
 
#control-U门,前3位为参数，第四位为作用的qubit，后两位是目标位和控制位
circuit.cu(pi/2,pi/2,pi/2,0,1,0)
circuit.cu(0,0,pi/2,1,0,1)
 
#测量
circuit.measure_all()
 
#电路可视化，以mpl形式输出，会自动调节输出电路的大小
circuit.draw(output='mpl')

效果图：

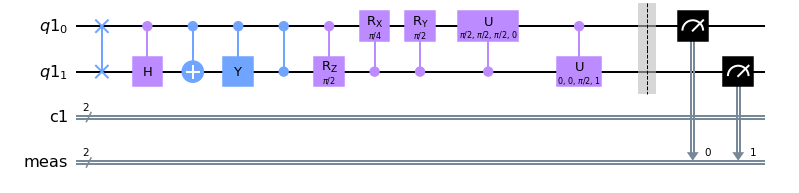
我们需要注意的是：

'QuantumCircuit' 也没有所谓的control-S（ $S^{+}$ ）,control-T( $T^{+}$ )门

3.三比特门

3.1 Toffoli门

#创建量子电路，其中qubit数是必选参数，bit是可选
circuit = QuantumCircuit(3)

#Toffoli门,qubit1,qubit2:控制位，qubit3:受控位
circuit.ccx(0,1,2)

效果图：

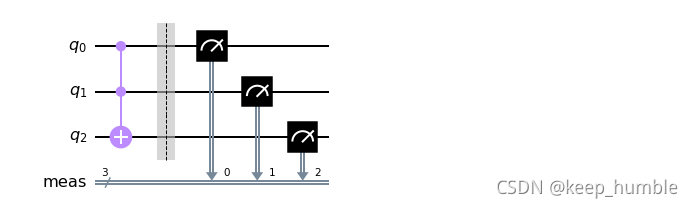
3.2 Cswap门


#创建量子电路，其中qubit数是必选参数，bit是可选
circuit = QuantumCircuit(3)
circuit.h(0)

#Toffoli门,qubit1:控制位，qubit2,qubit3:受控位,执行swap操作
circuit.cswap(0,1,2)
circuit.h(0)

电路图：

需要注意‘QuantumCircuit’是没有属性‘ccz’的

ccz是可以这样来实现： $Z=HXH$ （感谢boluoxia的评论，我之前咋就没想到呢）

# Create quantumcircuit
qc = QuantumCircuit(3)
qc.h(2)
qc.ccx(0,1,2)
qc.h(2)

4.量子态的初始化以及保真度计算

初始化量子态：

代码：

# 导入包
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import math
from math import pi
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, execute
from qiskit.tools.visualization import circuit_drawer
from qiskit.quantum_info import state_fidelity
from qiskit import BasicAer
# 实现一个单元格有多个输出，不要忘记！！！
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = 'all'



# Initializing a three-qubit quantum state
desired_vector = [
    1 / math.sqrt(16) * complex(0, 1),
    1 / math.sqrt(8) * complex(1, 0),
    1 / math.sqrt(16) * complex(1, 1),
    0,
    0,
    1 / math.sqrt(8) * complex(1, 2),
    1 / math.sqrt(16) * complex(1, 0),
    0]

# Create quantumcircuit
qc = QuantumCircuit(3)
    
#量子态初始化，将第1,2,3个qubit转换为我们想要的叠加态desired_vector
qc.initialize(desired_vector, [0,1,2])

# 指定模拟器statevector_simulator
backend = BasicAer.get_backend('statevector_simulator')

# 执行线路
job = execute(qc,backend)

#获取状态向量，get_statevector和statevector_simulator是对应的
qc_state = job.result().get_statevector(qc)

#计算保真度
state_fidelity(desired_vector,qc_state)

5.Reset

reset()函数可以在计算过程中，将qubit重置为 $|0\rangle$ ，reset不是一个酉操作，是一个不可逆的过程

# Create quantumcircuit
qc = QuantumCircuit(3)
qc.h(1)  
# 将qubit1重置为|0>
qc.reset(1)

效果：

参考资料：

Elementary Operations — Qiskit 0.11.1 documentation (sooluthomas.github.io)https://sooluthomas.github.io/testTranslation/terra/summary_of_quantum_operations.html#single-qubit-gates

二、量子状态的表示和单量子比特门_上官永石的博客-CSDN博客https://blog.csdn.net/qq_36793268/article/details/110352448