【Blender】贝塞尔曲线(Bezier)和nurbs(NURBS)曲线有什么关系吗？

【Blender】贝塞尔曲线(Bezier)和nurbs(NURBS)曲线有什么关系吗？

【Blender】贝塞尔曲线(Bezier)和nurbs(NURBS)曲线有什么关系吗？

• 贝塞尔曲线最早提出，也最简单，但只能全局修改。
• B样条曲线稍后提出，解决了贝塞尔曲线全局修改的喝到。
• NURBS曲线最后提出，定义最复杂，能表达的曲线最灵活。主要是解决B样条不能画椭圆、正圆和双曲线的问题。

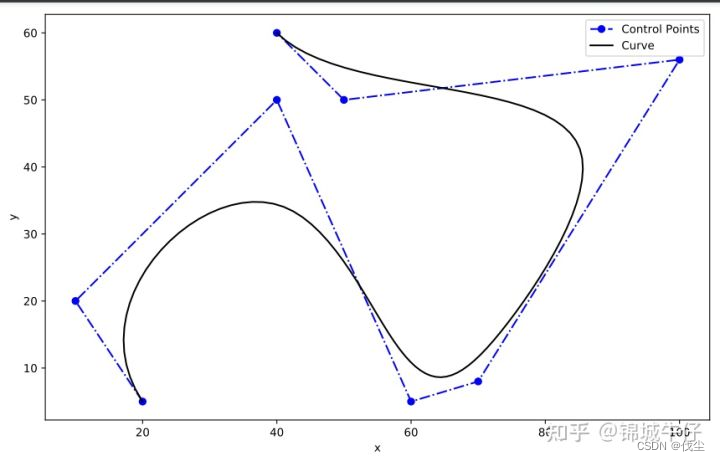
下面三个图是根据相同控制点使用不同曲线画出来结果。

1.NURBS曲线的公式：

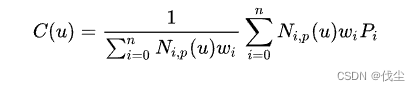
下面四个元素共同定义了NURBS曲线：

• 控制点，P0, P1, P2, …, Pn，共n+1个
• 权重值，w0, w1, w2, …, wn，共n+1个
• p阶
• 节向量U ，u0, u1, u2, …, um，共m+1个

并且 m, n, p 三者的数量关系满足：

2.B样条曲线的公式

如果所有权重值均等于1，则NURBS曲线将退化为B样条曲线。

下面三个元素共同定义了B样条曲线：

• 控制点，P0. P1, p2, …, Pn，共n+1个
• p阶
• 节向量U ，u0, u1, u2, …, um ，共m+1个

并且 [公式] 三者的数量关系满足：

贝塞尔曲线公式

如果B样条曲线的n=p（即，最大控制点下标＝阶数）， 节向量有2(p+1)个knot， 并且分别有p+1个knot在首尾固定。这个B样条曲线就退化成贝塞尔曲线。

仅需要控制点就定义了贝塞尔曲线的形态。