前言
我们知道,在二重积分中,换元积分如下:

但是很多人并不知道为什么是这样,所以一直记不住换元积分的公式。
引入
我们首先得明白,二重积分有点类似于求体积,f(x,y)就是高,D是底。然后积分,就是求和。将这个体积分成无数个小竖块,每一个小竖块都看成一个长方体,底面积就是dxdy,高就是f(x,y)。
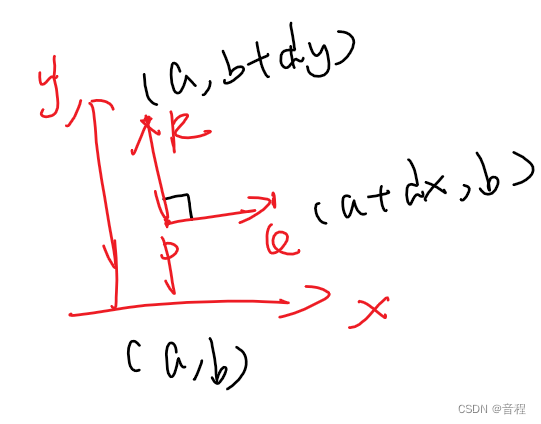
如下:下面是在计算以PQ,PR围成的面积,即dxdy。然后在这个小区域里面,它的高看成了长方体,即高都一样,而且使用了P点的高f(x,y)来代替。
现在,我们要换元:

此时,要记住,通过f,g这两个映射,x,y唯一确定了u,v,即相当于就是P,Q,R这三个点,在u,v坐标系里面都会映射为相应的点,如下:


可以看到,此时底面不一定是长方形了,通用的说,其实应该是一个平行四边形!!!
推导
你自己想想,我们现在其实就是要求映射后的面积是多少,即那个平行四边形的面积,然后乘以高,就可以完成映射后的积分啦。
平行四边形面积,即向量叉乘,也即两个二维列向量组成的矩阵的行列式的面积的绝对值。

然后,我们可以使用,偏导数定义:

注意,上面忽略了无穷小量,因为在有更大的量还存在的情况下,无穷小量没有用。

然后利用行列式性质,将dxdy可以提出来,我们就得到了上述式子。而上述式子就等于dudv,即平行四边形的面积为dudv。然后我们就得到了换元公式。

疑惑
为什么在原坐标系x,y中,dx,dy是长方形,是和坐标轴x,y轴方向一样的,但是在u,v中,du,dv就变成了斜的?其实,积分是求和,是无数个小竖块体积叠加,至于那个底是正方形还是长方形,甚至平行四边形重要吗?只要你能算出那个底面积,就都可以。
另外一个问题:从另外一个角度思考:将底面积从x,y轴,映射到u,v轴,然后高也映射过去,然后再在u,v轴计算体积,是没有雅可比矩阵的啊,为什么两者会相差一个雅可比矩阵呢?原因很简单,变换其实有可能导致体积变化,而不是你想象得那样,两者体积一毛一样。









 本文深入解析二重积分的换元法则,通过直观的几何解释和数学推导,阐述了在不同坐标系下底面积的表示变化,并解答了为何换元后会出现雅可比矩阵的问题。关键在于理解积分的本质是求和,底面积形式的变化反映了坐标变换对体积的影响。
本文深入解析二重积分的换元法则,通过直观的几何解释和数学推导,阐述了在不同坐标系下底面积的表示变化,并解答了为何换元后会出现雅可比矩阵的问题。关键在于理解积分的本质是求和,底面积形式的变化反映了坐标变换对体积的影响。

















 6640
6640

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










