基于FPGA的数字图像处理【2.2】

4.流水线装填与清空
        虽然流水线是一个并行的计算结构，每一级都有单独的电路单元来实现，并且与其他级是并行运行的，但是从数据流的角度，最好把流水线看成串行的结构。与串行处理直接相关的是流水线的等待时间，它是指从数据输入到产生相应的输出所用的时间。这个等待时间的观点主要是基于源驱动的概念。
        从目标驱动的角度看，等待时间意味着必须在输出前的一个预先指定时间内将数据输入到流水线结构中去。这段时间称为流水线的装填。如果输出是同步的，那么可以在输出端需要数据前的一个预设的时间开始装填。但是，当数据消耗点以异步方式请求数据时就不能使用这种方法。这种情况下，有必要使用数据装填流水线，然后再装填流水线完成后阻塞流水线直到输出端需要数据。如果不是在每个时钟周期都需要存在有效数据，那么源驱动处理也可能被阻塞。
        在装填区间，有效的数据正在流水线上传播，因而在这区间，流水线输出是无效的。与装填对应的一个概念是流水线清空，在输入端数据结束之后继续进行运算直到相应的数据输出。装填和清空的结果是使流水线操作需要的时钟周期比数据元素的数目要多。
        在很多时候，流水线填充和清空时间决定了图像处理算法的实时性。一个典型的例子是二维卷积运算。对于窗口尺寸为n×n的图像处理任务，在理想情况下，我们需要等到前n行和前n列图像数据流过（再次之前必须对这些数据进行缓存）流水线才有第一个数据输出。这个数据缓存过程也是流水线的填装过程。
        图4-6是流水线运算的一个实例：对分辨率为640×512的图像进行3×3膨胀运算，采用流水线方式。

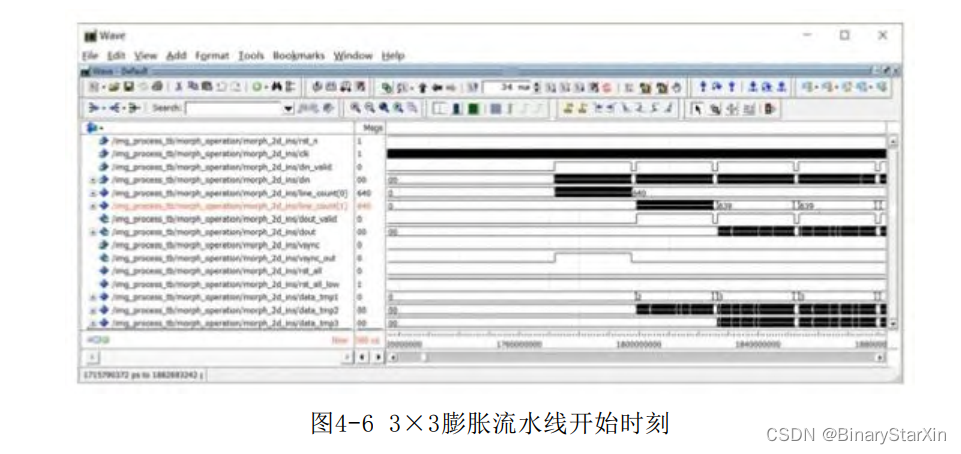
        3×3的流水运算需要至少3行的数据进行运算，因此每帧的前两行数 据 时 间 为 流 水 线 装 载 时 间 。 图 4-6 中 ， 装 载 的 数 据 装 入line_count(0)和line_count(1)，前两行为流水线装载过程，装满一行图像后停止装载，dout有效数据开始输出，这个时候流水线已经正式开始流水运算，在流水运算的过程中，装载器的数据个数是不变的，这也符合流水线的设计初衷：每个时钟处理一个像素。
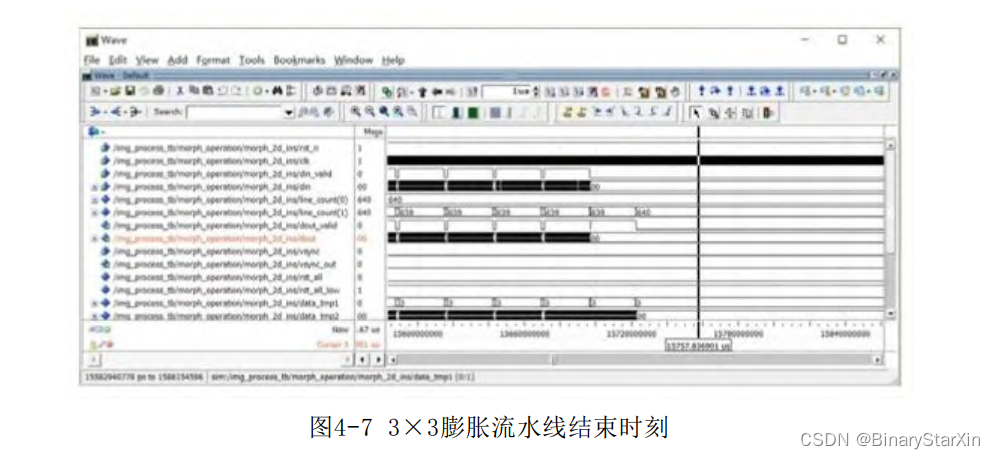
        理论上，流水线也有对应的卸载过程，装载发生在图像的最后两行。但是，如果不考虑边界，就可以略去卸载过程，也就是不处理流水线上最后过来的两行，如图4-7所示。
        在新的一帧到来时，重置流水线（由输入场同步信号进行重置），等待再次装载，如图4-8所示。
        流水线的装载时间决定了整个流水线的等待时间，也就是整个算法的开销。理论上，对于上述情况，整个开销为2行图像的装载时间，在不考虑边界的情况下，算法的延迟为1行图像，这是由于我们默认第一行清零。

4.1.2 并行阵列

        在并行阵列型电路中，多组并行排列的子电路同时接收整体数据的多个部分进行并行计算。并行阵列型电路中的子电路本身可以是简单的组合电路，也可以是复杂的时序电路例如上面提到的流水线型电路。如果受逻辑资源限制，无法同时处理全部数据，那么也可以依次处理部分数据直到完成全部数据的处理，如图4-9所示。

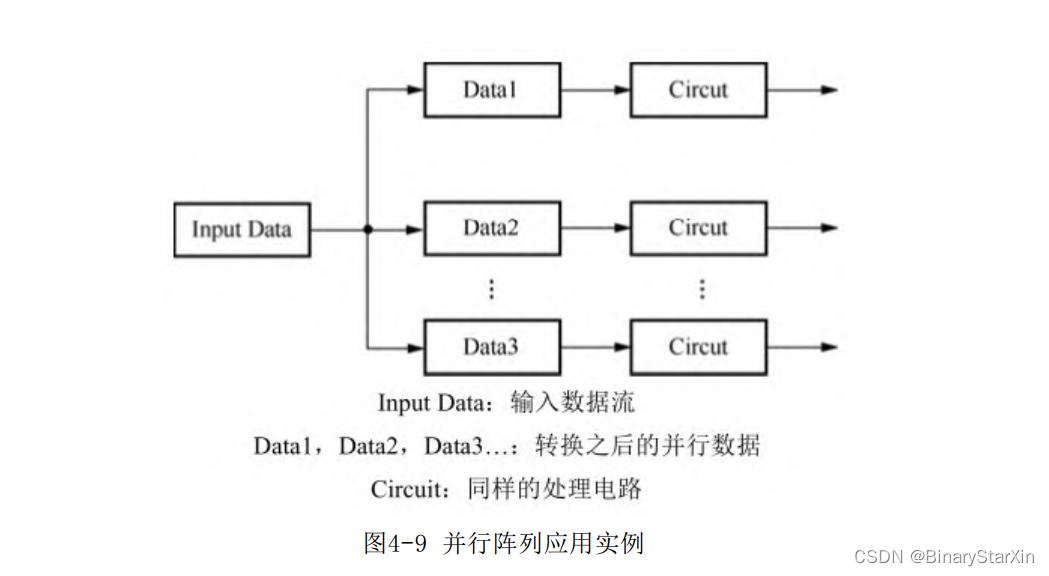
        和流水线共享电路的思路不同，并行阵列电路对于每个处理数据都生成一个处理电路，这无疑更大地提高了电路的处理速度，但是也带来了更大的资源消耗，是用面积换取速度原则的又一体现。如果系统设计对资源消耗相对不敏感，但是又需要较快的处理速度时，那么我们会选择并行结构来完成。

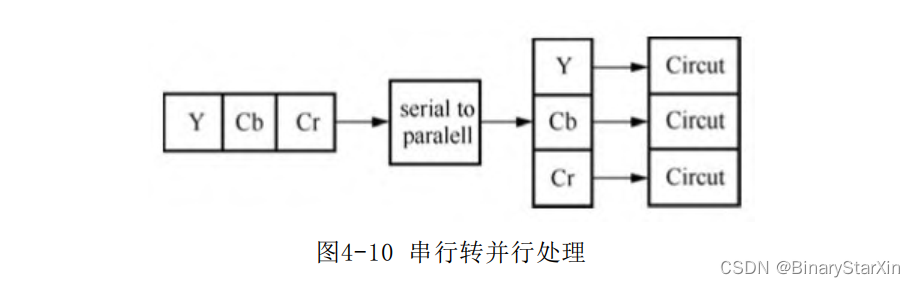
        并行阵列的一个典型应用是多通道像素同时进行处理，对一个串行输入的RGB通道或是YCbCr通道的视频流，首先做一个串并转换，接着复制处理逻辑对三个通道同时做处理。这样理论上可以得到3倍的速度提升，如图4-10所示。其中，serial to paralell是串并转换模块。

4.2 计算技术

        计算技术也是图像处理的核心技术之一。在软件算法设计和调试完成之后，需要将软件的算法映射到FPGA中去，由于软件和硬件的设计差异性，相当一部分算法在映射前需要通过等效转换，近似计算等硬件计算技术来转换成硬件易于实现的方式，从而达到逻辑资源消耗和时序，以及误差与消耗的平衡。本节将介绍几种常用的硬件计算技术。

4.2.1 算法转换

1.定常数转换
        在乘法和除法运算中，经常会遇到乘数、被乘数或分子与分母是常数的情况。直接调用乘法器或除法器当然可以解决这个问题，但是这会消耗一定的DSP运算单元，而DSP单元往往是FPGA里面比较少的资源。对于定常数，可以通过一定的转换将其转换为移位和加法运算，从而减少乘法器和除法器的使用。下面列举几个常用的例子。
考虑以下乘法运算的实现：

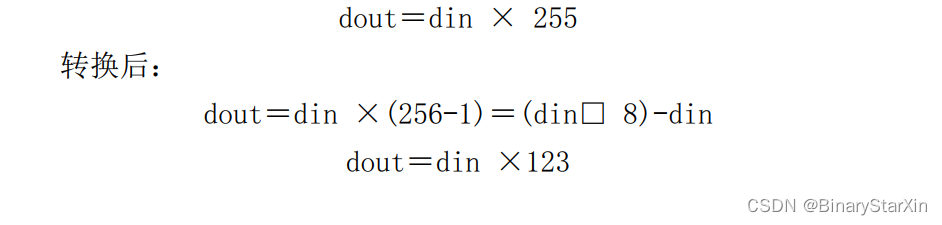
        扩展的位宽也决定了最终计算的精度，这个位宽越大，精度越高，但是也会消耗相对多一点的资源，实际应用中根据精度需求进行选择。
2．不等式等效转换
        不等式等效转换是利用不等式，将复杂的算法转换为较为简单的等效不等式。这对去除根号和除法等FPGA难以处理的算法十分有用。考虑下面的两个例子：

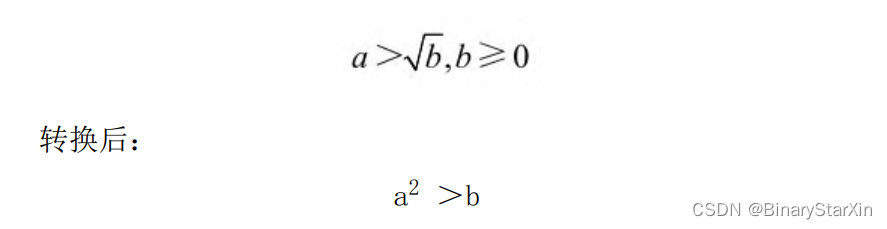
转换后，将开根号运算转换成乘法运算，直接调用FPGA内部的乘法器即可实现。

除法器在FPGA里面是比较昂贵的资源，上述转换将其化为乘法运算。

4.2.2 近似计算

        直接计算函数的一种替代方法是在感兴趣的作用域内，用另外一个较为简单的能得到相似结果的函数进行近似。与算法转换不同的是，算法转换是不会带来任何原理的误差，而近似则会带来一定的计算误差。通常情况下，在误差允许的范围内，采用近似计算带来的明显优势是计算复杂度的降低及资源消耗的降低。
1．截断
        用位数较少的近似值来代替位数较多或无限位数的数时，要有一定的取舍法则。在数值计算中，为了适应各种不同的情况，须采用不同的截取方法。
        经常使用的截断方法就是四舍五入。四舍五入通常应用在需要对中间输出结果进行截断时（一般情况下，我们会在前面的计算步骤中预留一定的计算精度。）四舍五入法的基本原则是，若舍去部分小于保留部分最后一位的一个单位的二分之一时，则采用去尾法处理，使所保留的数不变。实际上，对于FPGA来讲，处理的都是二进制数据。
        因此，在小数位的第一位的值是0还是1决定了是否对结果进行进位。一个简单的例子如下：（DW-1～4为整数位，3～0为小数位）assign dout=din[3]？din：(din[DW-1：4]+1'b1)：din[DW-1：4]；
2.泰勒近似
        在数学中，泰勒公式是一个用函数在某点的信息描述其附近取值的公式。如果函数曲线足够平滑，在已知函数在某一点的各阶导数值的情况下，那么泰勒公式可以用这些导数值作为系数构建一个多项式来近似函数在这一点的邻域中的值。泰勒公式还给出了这个多项式和实际的函数值之间的偏差。
        泰勒公式定义如下：对于正整数n，若函数f(x)在闭区间[a,b]上n阶连续可导，且在(a,b)上n+1阶可导。任取x∈[a,b]，它是一定点，则对任意x∈[a,b]成立下式：

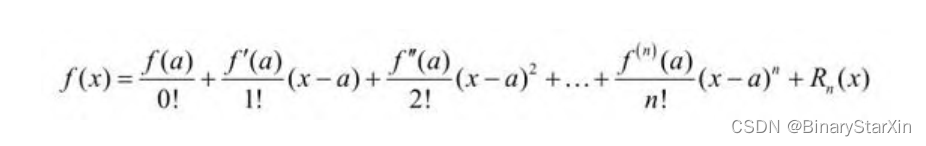
        其中，f（n） (x)表示f(x)的n阶导数，多项式称为函数f(x)在a处的泰勒展开式，剩余的Rn (x)是泰勒公式的余项，是(x-a)n 的高阶无穷小。
        当高阶项的数量级相对于低阶较小时，可以把高阶项去掉作为函数的近似。泰勒近似也称为多项式逼近。
        使用泰勒公式展开的一个要点是如何选取截断阶数。这往往是由事先规定的计算误差决定的。以下是一个用泰勒展开进行近似计算的实例。现在考虑对除以3的运算用泰勒近似进行计算，即

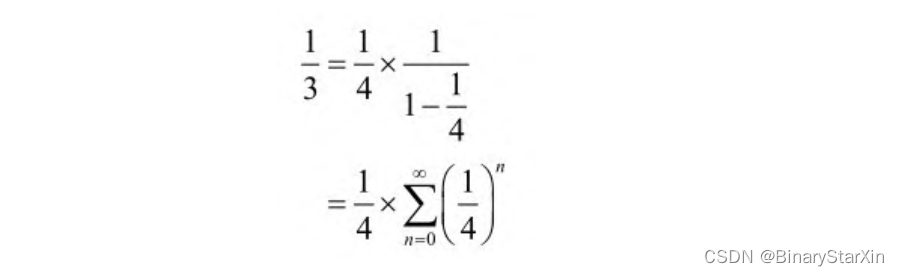
若要求计算误差不大于10-4 ，则取前5阶即可达到要求，展开如下：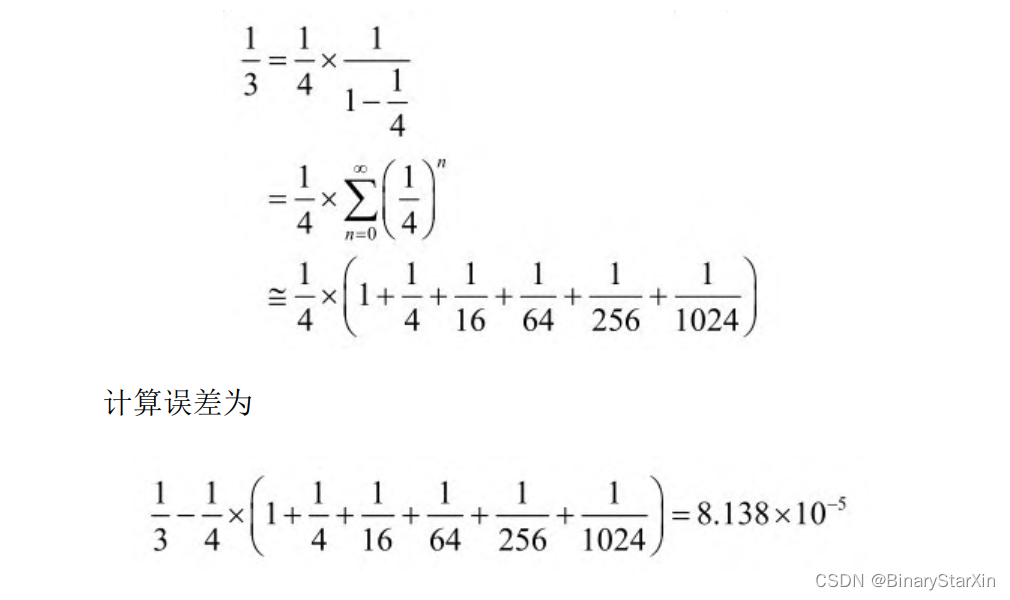

3.浮点转换
        如果不采用拥有内部浮点硬核的FPGA，那么用FPGA作为浮点运算的开销是巨大的，因为这会消耗巨大的逻辑资源。在计算精度能满足一定要求的情况下，通常会选择将浮点运算转换成定点运算。在接下来的浮点计算的章节将会详细介绍浮点计算。

4.2.3 增量更新

        增量更新是指在进行更新操作时，只更新需要改变的地方，不需要更新或者已经更新过的地方则不会重复更新，增量更新与完全更新相对。增量更新在流水线处理中，特别是二维卷积处理中特别有用。这是由于在两个连续的卷积窗口中有大量的相同元素，如图4-11所示。

        假定要计算连续5个数据流的和值，在上一个时刻，这5个待计算的 数 值 是 a1',a1,a2,a3,a4 ， 在 本 时 刻 ， 这 5 个 待 计 算 的 数 值 是a1,a2,a3,a4,a5。中间有4个计算值都是不变的，这时候如果再调用4个加法器进行5个数的加法就有点浪费资源。正确的做法是取上一个时刻的计算和值加上首尾的差值。这种增量更新的方法对于较大尺寸的计算带来的优势更加明显。
        类似的技术可以用于递增的确定放射变换的输入位置。考虑下面的变换：

这种情况下有必要增加保护位，以防止舍入误差累积后逼近A和D。

4.2.4 查找表

1.查找表的定义
        在计算机科学中，查找表是用简单的查询操作替换运行时计算的数组或者associative array这样的数据结构。由于从内存中提取数值经常要比复杂的计算速度快很多，因此这样得到的速度提升是很显著的。
        一个经典的例子就是三角表。每次计算所需的正弦值在一些应用中可能会慢得无法忍受，为了避免这种情况，应用程序可以在刚开始的一段时间计算一定数量的角度正弦值，譬如计算每个整数角度的正弦值，在后面的程序需要正弦值的时候，使用查找表从内存中提取临近角度的正弦值而不是使用数学公式进行计算。
        由于查找表的高效率与方便易用性，它在实时性要求比较高的嵌入式系统中得到了广泛的应用。在FPGA中，主要是以下两种情况会用到查找表：一种是逻辑的时序要求非常高，例如，若用Cordic计算或是其他计算方式，则其延时不能满足要求时；另一种是计算的复杂度非常高，需要消耗相当一部分逻辑资源，而查找表只需建立一块的存储器，这可以用FPGA的片内存储器来构建，仅仅消耗很小一部分逻辑资源。

2.查找表的构建
        使用查找表的首要问题就是输入表的构建。输入表的构建需要首先得到输入函数的有效定义域，其次是将输入的定义域进行等分。这时就需要考虑等分步长，必须在计算精度和表的大小之间做一个最佳权衡。还有一个需要考虑的问题是，通常情况下，待求函数通常是用实数表示的，我们会首先将其转化为整形，这个过程也会带来一定的舍入误差。
        虽然查找表在种地精度时很有效，但是随着输入宽度的增加，表的尺寸呈指数倍增长。实用的查找表尺寸需要减小输入的精度，一个简单的方法是简单地删除最低位来实现。没有必要对输入进行舍入，因为表的内容可以根据保留为作用域中的函数的适当值设置来获得最好的结果。

        另外一个减小输入尺寸的方式是考虑对称性，例如对于对称的正余弦函数，对于有效定义域[0～2π]，只要考虑第一象限范围。在输入进入查找表之前首先进行象限判断，并保存其象限信息。同时，将其转换到第一象限，查表后根据象限信息恢复实际计算值。这样就将查找表的输入范围减小到原来的四分之一。
3.查找表应用示例
        下面是一个用查找表来实现正弦函数sinx的示例。查找函数的生成可以用MATLAB或者VC等软件工具生成。对于Altera的器件来说，可以生成mif或hex格式的文件。以下是以MATLAB来生成mif文件的示例。
        正如前面所述，只需建立 范围内的正弦函数查找表即可。这里取步长为0.1°，将输出值整个[0：1]范围扩展到[0：16384]，即左移14位。

clear all
close all
clc
t=[0:0.1:90];%输入范围0～90°，步长0.1°
x=pi*t/180;sin_val=sin(x);%取出正弦数组
fid=fopen('sine.mif','wt');
fprintf(fid,'width=14;\n');%转换后的数据位宽14位
fprintf(fid,'depth=1024;\n');%共900个点，深度最少需要1024
fprintf(fid,'address_radix=uns;\n');%地址是无符号类型
fprintf(fid,'data_radix=dec;\n');%数据是十进制类型
fprintf(fid,'content begin\n');
for j=1:901
i=j-1;
k = round(sin_val(j)*16384);
if(k==16384)
k=16383;
end
fprintf(fid,'%d:%d;\n',i,k);
end
fprintf(fid,'end;\n');
fclose(fid);
FPGA端例化一个ROM来实现查找表的存放。模块定义如下：
module sin_lut (
address, //地址
clock, //时钟
q); //输出
parameter DW = 15;
parameter AW = 10;
parameter DEPTH = 1024;
测试模块如下所示：
'timescale 1 ps / 1 psmodule sin_lut_tb;
parameter DW = 15;
parameter AW = 10;
parameter ADDR_MAX = 900;
parameter const_half_pi = ADDR_MAX-1; //90°地址
parameter const_pi = ADDR_MAX*2-1; //180°地址
parameter const_double_pi = ADDR_MAX*4-1; //360°地址
reg [AW+2-1:0] address_tmp;
reg [AW-1:0] address;
reg clock;
wire [DW-1:0] q_tmp;
reg [DW+1-1:0]q_tmp1;
wire [DW-1:0] q;
initial
begin
clock ＜= 1'b0;
address_tmp ＜= {AW+2{1'b0}};
end
sin_lut u0(
.clock(clock),
.address(address),
.q(q_tmp)
);
always @(clock)
clock ＜= #50 ～clock;
//根据输入地址判断输入请求的象限位置，根据象限映射到新
的地址always @(posedge clock)
if(address_tmp==const_double_pi)
begin
address_tmp ＜= {AW+2{1'b0}};
address ＜= {AW{1'b0}};
end
else
begin
address_tmp ＜= address_tmp+1'b1;
if(address_tmp＜=const_half_pi)
address ＜= address_tmp[AW-1:0]; //第一象限 地
址不变
else if(address_tmp＜=const_pi) //第二象限
address ＜= const_pi-address_tmp;
else if(address_tmp＜=(const_pi+const_half_pi))//第
三象限
address ＜= address_tmp-const_pi;
else
address ＜= const_double_pi-address_tmp; //第四
象限
end
always @(posedge clock)
if(address_tmp＜=const_pi) //前两象限 输出大于0
q_tmp1＜= {1'b0,q_tmp};
else
q_tmp1＜= {DW+1{1'b0}} - {1'b0,q_tmp}; // 后 两 象 限
输出小于0assign q = q_tmp1[DW-1:0];
endmodule