前言
要解决动态系统的建模问题,首先要对研究对象进行分析,分析其物理特性和动态表现,在此基础上建立数学模型,然后在数学模型的基础上设计控制器,最后就是做测试
一.特征值和特征向量
对于一个给定的线性变换A,它的特征向量v经过这个线性变换的作用后得到的新向量仍然与原来的v保持在同一直线上,但长度或方向可能会变化,即
表示该特征向量的长度在该线性变化下缩放的比例,称为特征值。
特征向量的求法:
由求得特征值,然后代回
求出v内的关系,然后找v的一组解即可
应用:特征值和特征向量重要的应用是化对角矩阵,然后用于解耦


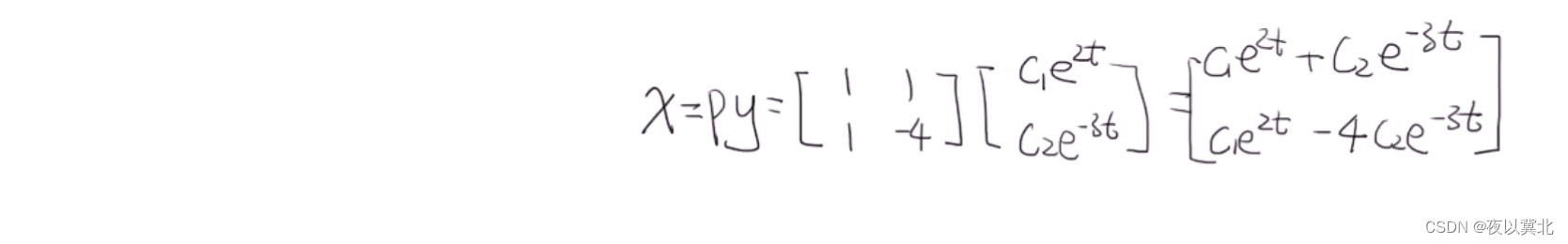
二.线性化——泰勒展开
(线性系统满足叠加原理)
线性化是在某一点处的线性化
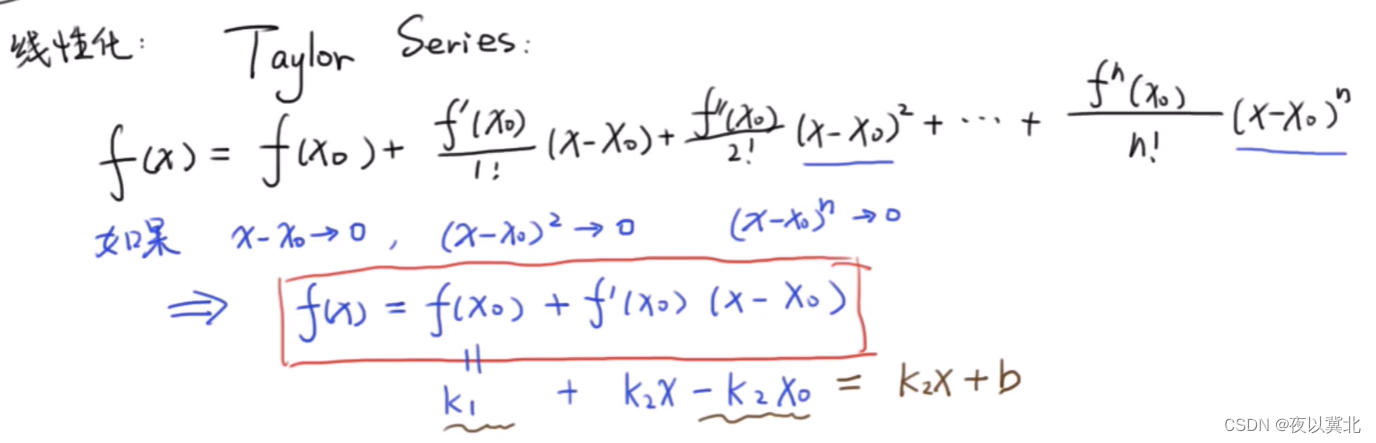
例1:

三.卷积的理解
卷积就是叠加原理,将一个连续的作用力分解成多个突变的作用力,然后某一时刻的效果就是所有作用力(不管是现在还是以前的)在此刻作用出来的效果叠加在一起,只要前面的分解足够小,就能将累加转为积分。
系统:对一个刺激能产生一个响应,这也是冲激函数的重要之处,就是体现在其宽度趋向于无穷小,然后过系统时所产生的效果就只有那一个冲激在系统中,不存在其他的叠加,所以要想得到一个系统的传递函数,就放一个冲激函数过一遍系统,得到的响应函数就是传递函数。
系统作用于输入信息是怎么理解呢?相信你一定听过“现场音质”这个概念,其实就是原声在现场环境的叠加下的音质,你任意时刻听到的声音是前面一点声音和现在声音在现场环境下进行叠加的结果,卷就是一个冲激(极短的原唱)的响应(在现场环境下的效果),积就是将响应进行叠加,这就是一个很有趣的应用——就是在待还原现场中给一个冲激,得到一个响应函数,用这个响应函数来卷积原唱,就能还原现场现场音质,这就是原声在环境中的作用形成的效果,现场环境就是系统。
| 输入信号: | 响应信号: |
| 右移i个单位: | |
| 乘上A倍: | |
是底,
是在连续函数f(t)上取
的位置的值,即高,底乘高等于面积
则表示一种冲激对应的响应结果,当
时,
,将到目前为止所有的冲激在当前时刻下的响应累加起来就是当前时刻的总响应,只要认可上表中最后一条的输入信号无误,而
的响应就是对应
,累加形式也是一样的。
四.拉普拉斯变换
补充:拉普拉斯变换的重要作用就是将时域的微分方程变成复频域的代数方程,注意后面的拉普拉斯变换计算都从0开始的原因是一般都将信号考虑从0开始,不考虑时域为负数的情况。
傅里叶变换展示一个函数中出现哪些频率的正弦波,
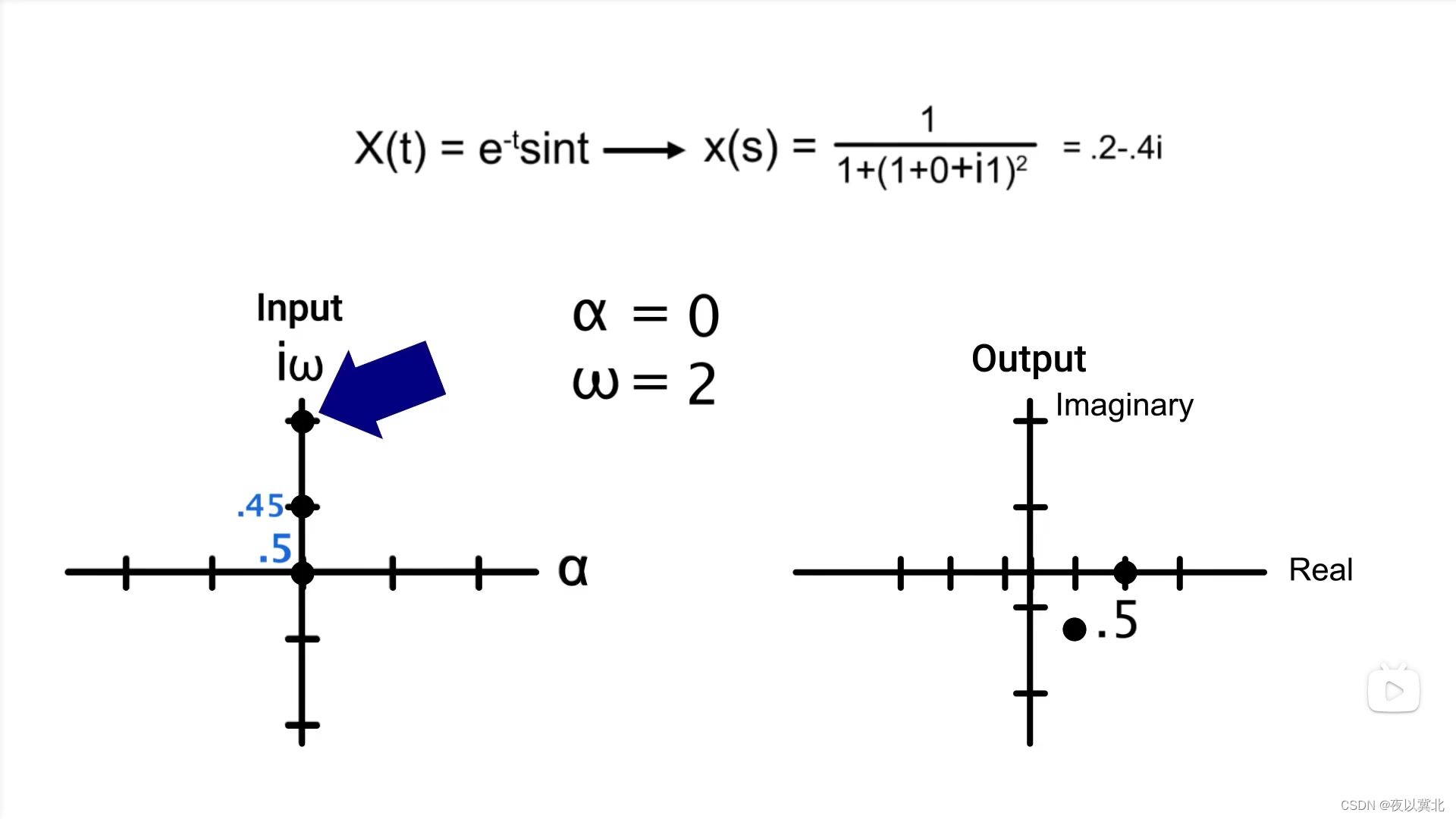
例如,显然X(w)的输出只与w有关,且为复数,因此要用二维坐标系来表示(下图的右边),再计算模值(幅值)就可以得到下图左边的w与幅值的关系图,即傅里叶变换的幅值图
当w=0时,右式就是x(t)在整个区间的积分,即X(0)表示面积

而拉普拉斯变换展示一个函数中的正弦波和指数衰减
,
是衰减项
例如,显然X(w)的输出与w和
有关,且复数项都有w和
,因此要用四个轴来表示,首先是得到一个复数和上面一样用一个二维坐标表示(下图的右边),然后计算模值就可以得到关于w、
和幅值之间的关系图(下图左边)
下图左边就是上图虚轴上的值,右边就是傅里叶变换那里的表示形式,通过俯视的视角看成一条线就是对应左边:
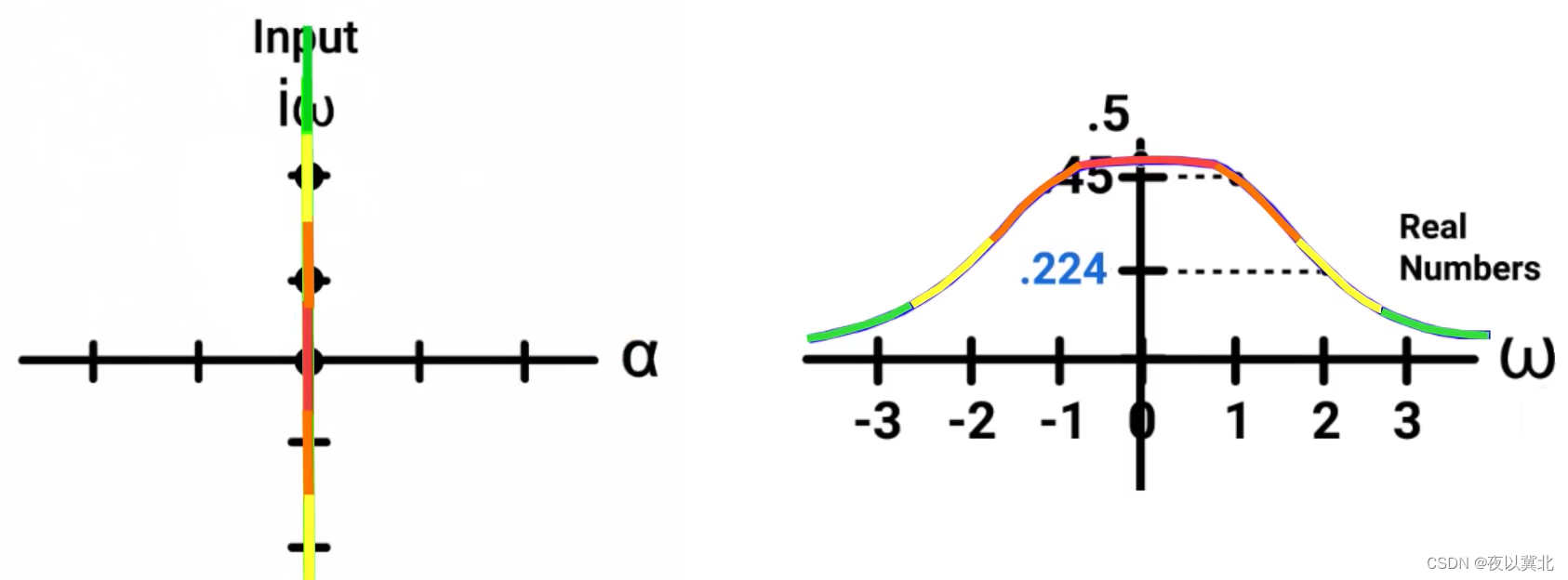
每一个都对应一种傅里叶变换,所有
的傅里叶变换就会形成下图,即拉普拉斯变换
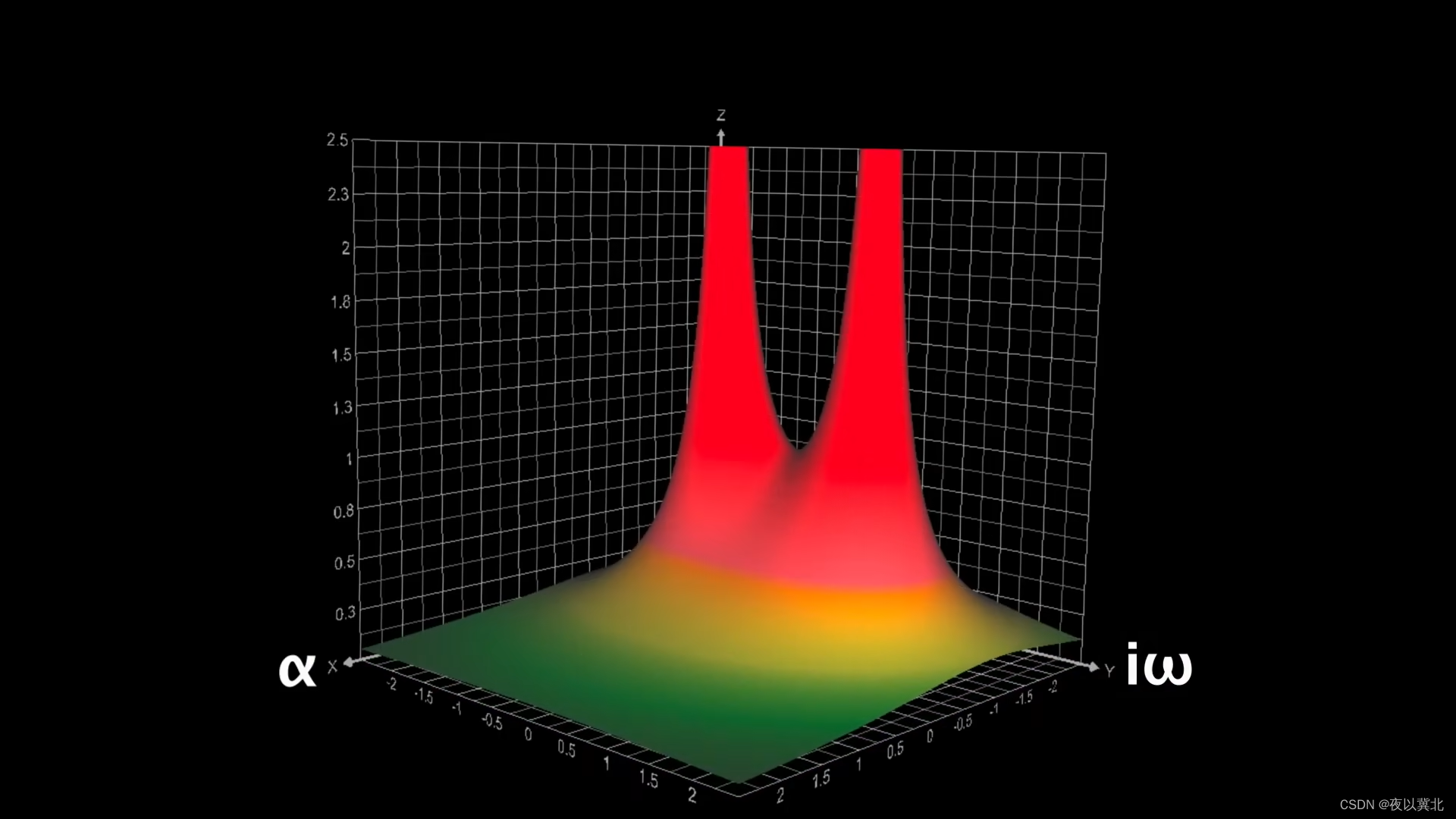
上图无穷高的尖峰就是极点,极点的意义在于将极点对应的复数值代入拉氏变换就是得到,当平面沿着
扫描时,扫描到极点的位置就停止了,此时
这个指数项系数大于1,后面的傅里叶变换不再收敛,拉普拉斯变换也就不存在,这也就是收敛域的概念
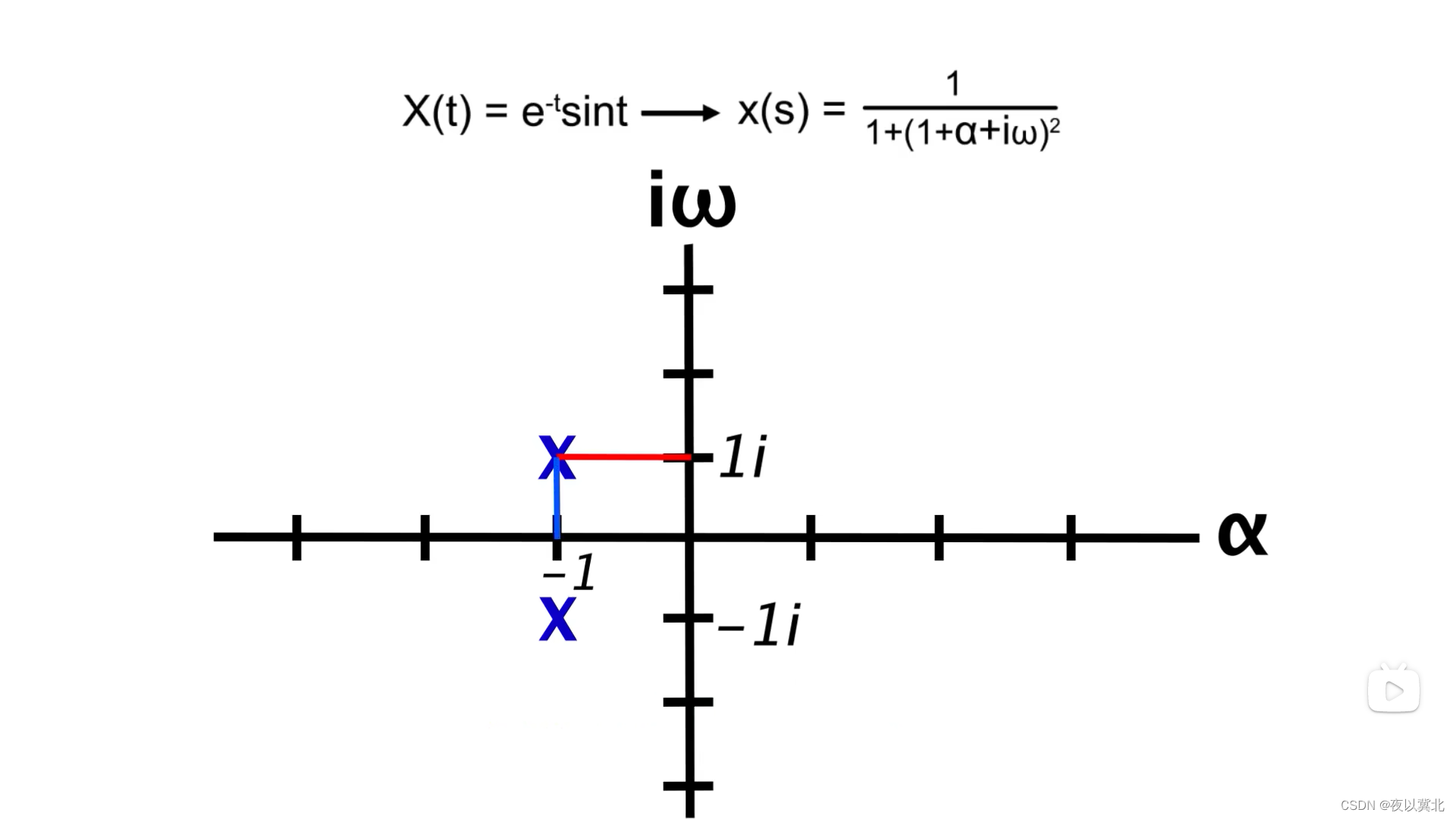 上述是一个极点图,点(-1,1i)表示原函数既有频率为1的正弦波,也有-1的衰减分量
上述是一个极点图,点(-1,1i)表示原函数既有频率为1的正弦波,也有-1的衰减分量
由此可知道如果极点只在虚轴上,就说明原函数只包含正弦曲线,极点里原点越远,说明正弦频率越高,如果极点只在实轴上,就说明原函数只包含指数函数,极点离原点越远,说明衰减得越快。


五.控制理念
在经典控制理论和现代控制理论当中,大部分的研究对象就是常系数线性微分方程,对应的系统就是线性时不变系统

因此,控制基本理念:通过设计不同的系统输入U(s),用U(s)去乘以传递函数G(s),这个时候去配置系统的极点,让系统的极点到达我们希望它到达的地方,从而达到控制系统输出,因为从上面可知 f(t)的衰减量和振荡量 与 极点的实部和虚部 是对应的。
六.一阶系统的单位阶跃响应和时间常数
其实就是研究将单位阶跃做为输入,通过一阶系统的输出,重点就是时间常数


补充新角度看单位阶跃响应
一阶线性时不变系统
传统角度:在自动控制理论当中,可以用传递函数来分析系统,对上述式子两边做拉氏变换得到,输入还是单位阶跃,对应的拉氏变换为
,在上述一阶系统对应的响应在复频域为
,时域为
,然后求时间常数;
回到最开始,如果只考虑的情况,那么系统函数可以重新表示为
,在图像上就是斜率为-a,截距为a的直线
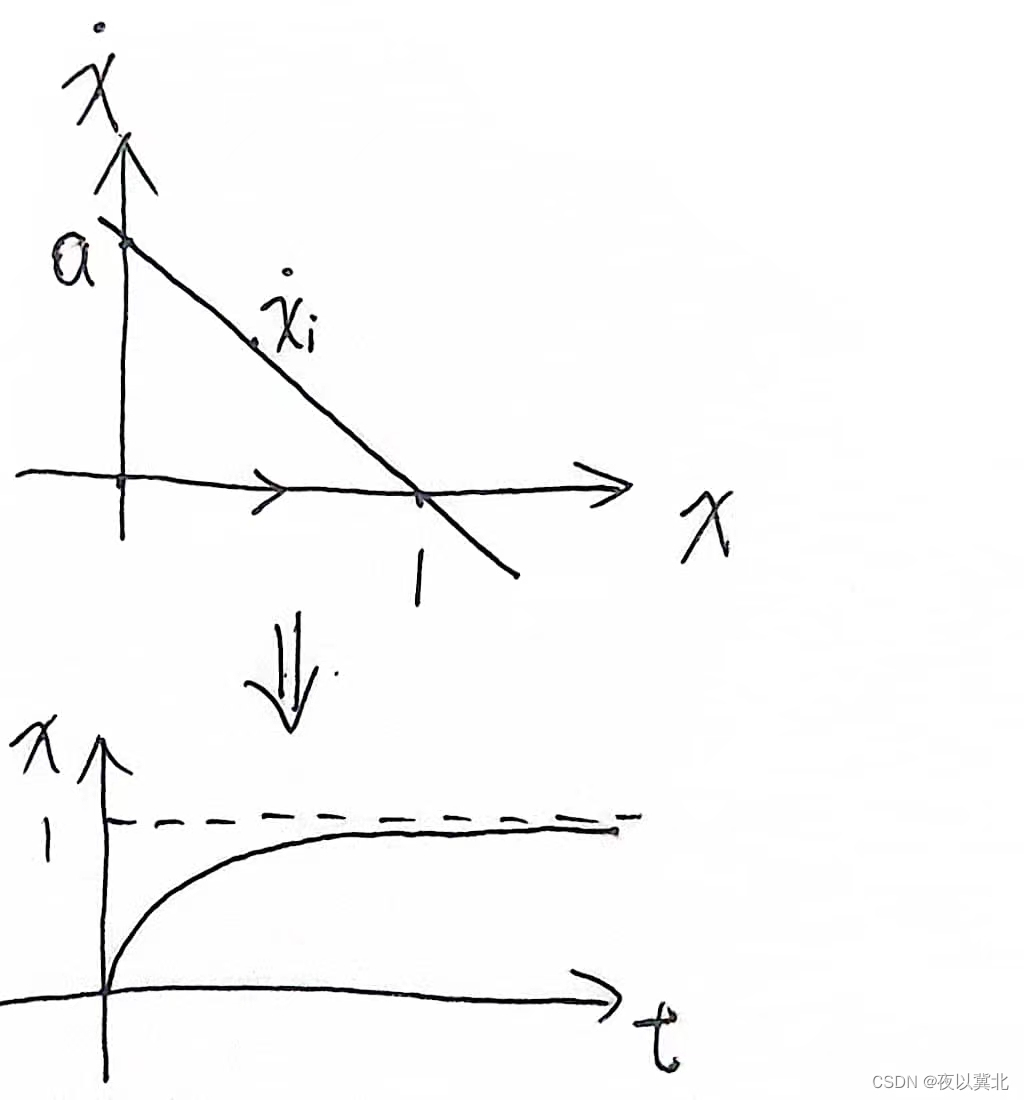
上图表示x与的关系图,以及对应的x的变化图,主要看上图,当初始值
时,
,即导数大于0,表现到上图就是右移,而随着右移
会逐渐下降,表现到图上就是移动变缓慢,直到x=1时也停止移动。






















 3330
3330











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










