作者:aminzeng2022
目录
1 基本概念
在学习和工作中,我们工科人必然都会遇到各种各样的变换,比如傅里叶变换、拉氏变换、Z变换、线性变换等,总是让人感觉头大。虽然可以运用,但总像隔着一层迷雾,让人有一种朦胧的感觉,好像抓住了又好像没有抓牢,当你想靠近它时,却发现还隔着一段距离。就跟追求喜欢的女孩子一样,可以跟你聊天吃饭,就是不答应做你女朋友,让你又爱又气。本系列文章命名为《从“根”上彻底理解各种变换》,就是想让大家彻底理解各种变换的原理,达到一步到位一劳永逸的效果,真正做到知其然且知其所以然。
为了做到从“根”上解决问题,需引入几个基本概念,这些概念也是大家所熟悉的,非常浅显明了,在这些概念的基础上,我们再给出变换的定义,大家就会有豁然开朗的感觉。
1.1 向量
向量有很多种定义,在几何中也叫作几何向量,在物理中也常称为矢量(如力、速度等)。但不管什么叫法,向量都具有两个必备的要素:大小和方向。所以只要满足大小和方向的定义,我们可以灵活地定义向量。
在本文中给出向量的定义:向量是具有大小和方向的一个量。
两个向量的大小和方向都相同,才说两个向量相等。向量可以由一组有序的数列表示,这组序列称为向量的坐标。
如:(a,b)可以表示一个二维向量坐标,(a,b,c)可以表示一个三维向量坐标,![]() 可以表示一个n维向量坐标,函数sin(x)在
可以表示一个n维向量坐标,函数sin(x)在![]() 上的无穷个函数值也可构成一个无穷维向量的坐标。所以函数是特殊的向量。
上的无穷个函数值也可构成一个无穷维向量的坐标。所以函数是特殊的向量。
向量坐标中的数是有顺序的,顺序不同向量也不同。如向量(a,b)和向量(b,a)不是同一个向量,向量(a,b,c)和向量(a,c,b)也不是同一个向量。
向量的大小(也叫模)等于向量坐标中各数的平方和再开根号。如向量A=(a,b)的大小![]() ;向量
;向量![]() 的大小
的大小![]() ;在
;在![]() 取值的向量A=sin(x) 的大小为
取值的向量A=sin(x) 的大小为![]() 。
。
向量的方向由多个角度来定义,通过向量坐标中的每个数与向量大小的比值的反余弦得到这些角度(余弦角)。比如二维向量A=(a,b)由两个余弦角确定其方向:![]() 和
和![]() ;三维向量
;三维向量![]() 由三个余弦角确定其方向:
由三个余弦角确定其方向:![]() 、
、![]() 和
和![]() ,以此类推,n维向量有n个余弦角表示其方向,无穷维向量有无穷个余弦角表示其方向。
,以此类推,n维向量有n个余弦角表示其方向,无穷维向量有无穷个余弦角表示其方向。
如果上述的向量相定义觉得有些抽象,我们可以通过简单的二维向量和三维向量来形象的理解,大家就会知道我们其实早已接触并掌握这些定义了,只是这里更普及抽象化一些。
在二维直角坐标系中,有一个二维向量A=(3,4),图1.1列出了该向量的大小和方向。
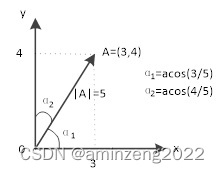
图1.1 直角坐标系下的二维向量
在三维直角坐标系下,有一个三维向量A=(3,4,5),图1.2列出了该向量的大小和方向。
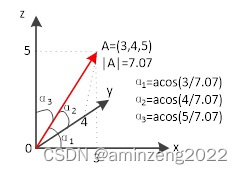
图1.2 直角坐标系下的三维向量
对于n维向量,虽然无法画出其坐标系,但可以自已补脑,在脑中想像一个n维直角坐标系,并在其中画出向量的其大小和方向。
1.2 向量投影
向量投影是两个向量之间的一种运算,形象理解见图1.3所示,从一个向量A的始点和终点向另一个向量B作垂直线,得到的线段长度即是向量A在向量B上的投影值,投影方向与向量B同向时,长度符号为正,反之符号为负。所以向量投影最终得到的是一个带符号的数值(标量)。
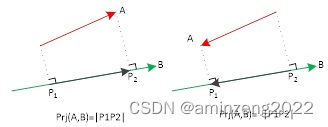
图1.3 两个向量的投影
图形可以帮助理解,但不易得到最终的值。要得到最终的值,还是得通过两个向量的投影运算(点积)得到其投影值。点积就是将两个相同维数的向量的对应坐标值相乘再相加,点积结果是一个标量。如:
向量A:![]() ;
;
向量B:![]() ;
;
向量A投影在B上的值(也就是A和B的点积):
![]()
像函数这种特殊向量就用积分的方式,如:
向量A=sinx,x∈[-π,+π];
向量B=cosx,x∈[-π,+π];
向量A投影在B上的值(也就是A和B的点积):
![]()
垂直:如果![]() ,我们就说向量A和向量B相互垂直。如图1.4中的向量A垂直向量B。
,我们就说向量A和向量B相互垂直。如图1.4中的向量A垂直向量B。

图1.4 向量A垂直向量B
投影(向量点积)的理解是从根本上理解变换的基础。因为从本质上说,各种变换的操作即是一种投影操作。所以,若对投影理解还不是很到位可以找相关资料再学习学习。
1.3 向量基
初次接触向量基可能觉得陌生不好理解,下面由浅入深开始讲解。
前面提到向量可由一组有序数列(即坐标)表示,向量基就是为了描述向量坐标而选择的一组特殊向量。也可以说有了向量基,才能得到向量的坐标值,否则向量只是一个具有大小和方向的量。
我们常见的直角坐标系就是由向量基构成。比如在平面直角坐标系中,二维向量A=(3,4),其中坐标值3和4代表的数值其实就是向量A在坐标轴x、y上的投影值,坐标轴x、y本质上也是向量,x=(1,0)、y=(0,1)。由x、y组成的一组向量就是平面直角坐标系的向量基[(1,0)、(0,1)]。有了这个向量基,向量A的元素3和4才有意义:
A在向量基中的(1,0)上投影值为3:x=3×1+4×0=3;
A在向量基中的(0,1)上投影值为4:y=3×0+4×1=4。
同理, [(1,0,0)、(0,1,0)、(0,0,1)]是三维坐标系下的向量基,此次类推,可得到n维坐标系乃至无穷维坐标系下的向量基。
向量基具有非唯一性、正交性、归一性和完整性等特点。
1.3.1 非唯一性
在一个n维空间中,向量基具有非唯一性。以二维空间举例,见下图1.5所示。在图1.5中,有两个坐标系:![]() 和
和![]() ,
,![]() 逆时针旋转45°后得到
逆时针旋转45°后得到![]() 。
。![]() 的向量基是[(1,0)、(0,1)],
的向量基是[(1,0)、(0,1)],![]() 的向量基是[
的向量基是[![]() 、
、![]() ]。将向量A在
]。将向量A在![]() 上进行投影,得到坐标(3,4);将向量A在
上进行投影,得到坐标(3,4);将向量A在![]() 上进行投影,得到坐标
上进行投影,得到坐标![]() 。
。

图1.5 二维空间下的向量基
通过坐标(3,4)和![]() ,都可得到向量A的大小为|A|=5。在两个坐标系中,向量A的余弦角是不同的,但A相对空间的方向是不变的。所以在两个不同的向量基下可表示同一个向量,说明向量基具有非唯一性。
,都可得到向量A的大小为|A|=5。在两个坐标系中,向量A的余弦角是不同的,但A相对空间的方向是不变的。所以在两个不同的向量基下可表示同一个向量,说明向量基具有非唯一性。
不难推断,在n维空间中向量基不仅具有非唯一性,而且具有无数个!
1.3.2 正交性
上面说向量基具有非唯一性,并不是说随意整几个向量就可以组成一个向量基。向量基必须具有正交性:向量基中任意两个向量相互垂直。只有向量基保证了正效性,向量的长度才能通过所有坐标值的平方和开根号得到。
比如图1.6中,由向量x1、y1组成的向量基是[![]() 、
、![]() ]。很明显,x1和y1不垂直,向量A在x1上的投影为
]。很明显,x1和y1不垂直,向量A在x1上的投影为![]() ,在y1上的投影为4,所以
,在y1上的投影为4,所以![]() ,所以坐标基[
,所以坐标基[![]() 、
、![]() ]不能用来表示二维空间的向量,因为基中的两个向量不垂直。
]不能用来表示二维空间的向量,因为基中的两个向量不垂直。

图1.6 不正交的向量基
在n维空间中的一个n维向量基[x1,x2,x3,⋯,xn]正交,则有![]() (其中k,l=1、2、3、⋯⋯、n,且k≠l)。
(其中k,l=1、2、3、⋯⋯、n,且k≠l)。
1.3.3 归一性
向量基的归一性就是指构成向量基的每个向量的大小都为1。如n维空间中的一个n维向量基[x1,x2,x3,⋯,xn],则有:![]() 、
、![]() 、
、![]() 、⋯⋯、
、⋯⋯、![]() 。
。
为什么要求向量基中的向量大小为1呢?这是为了用此向量基表示向量时保证向量的大小不变。如将平面直角坐标系的向量基定为[(2,0)、(0,2)](每个向理的大小都增大一倍),那么原来长度为5的向量A=(3,4) 在坐标系中投影就会得到新的坐标为A=(6,8),明显![]() ,向量A的大小也增大了一倍。所以不具有归一化性质的向量基表示向量时会改变向量的大小。
,向量A的大小也增大了一倍。所以不具有归一化性质的向量基表示向量时会改变向量的大小。
所以在上面图1.5中,另一向量基为[![]() 、
、![]() ],其中的每一个向量的大小都为1。
],其中的每一个向量的大小都为1。
后面会讲到的傅里叶级数的向量基:1、cosx、sinx、cos(2x)、sin(2x)、cos(3x)、sin(3x)、⋯⋯。每个基中向量在范围[-π,+π]上大小都不为1,在计算投影时必须要先对向量基进行归一化,使向量基中每个基的大小都为1。
1.3.4 完备性
向量基除保证正交性和归一性外,还要保证完备性。向量基的完备性是指n维空间的向量基应由n个相互正交的向量组成,少一个都不行!
在平面直角坐标系中,向量基含有两个正交向量,对应两个垂直的坐标轴;在三维直角坐标系中,向量基含有三个正交向量,对应三个垂直的坐标轴。以此类推,在n维空间中,向量基应包含n个相互正交的向量;对无穷维空间,向量基应包含无穷个相互正交的向量,这时要将所有正交的向量都找出来。
向量基不完备时不能准确表示向量的大小和方向,即变换会存在误差。
1.4 变换
在向量、投影和向量基的定义基础上,给变换进行统一定义如下:
变换即是将某个向量从一个坐标系(向量基1)投影到另一个坐标系(向量基2)上得到新的坐标值的过程。变换用图表示如下:
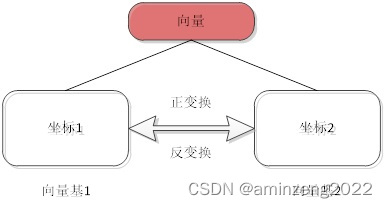
图1.7 变换原理框图
在变换的过程中,向量本身是不变的,只是表示方法不同而已。所以变换的前提是保证不论是用坐标1还是用坐标2,都能得到向量的大小和方向(绝对方向),且大小和方向是不变的。
这就好比我们用放大镜观察物体,看到的景象和用肉眼看到的是不同的,但真实的物体本身唯一的;又比如观察一个三维物体,从前面看和从侧面看,看到的形状是不同的,但物体是同一个物体;还比如我们最常用到的傅里叶变换,将信号从时域变到频域,看到的信息大相径庭,但代表的信号是同一个信号。
需要注意的是,投影计算时要在同一坐标系下。如从坐标1变换到坐标2,向量表示法要基于向量基1,向量基2中的向量表示法也要基于向量基1。回头看图1.5,坐标系1(X1OY1)的向量基是[(1,0)、(0,1)],向量A在坐标系1下的坐标是(3,4),坐标系2(X2OY2)的向量基是[![]() 、
、![]() ],其中
],其中![]() 和
和![]() 表示都是基于向量基1的。所以从坐标系1变换到坐标系2的得到新坐标为
表示都是基于向量基1的。所以从坐标系1变换到坐标系2的得到新坐标为![]() 。
。
同样道理,现在要将坐标系2下的坐标![]() 反变换到坐标系1下,就要得到向量基1中的向量在向量基2中的表示方法,然后再在坐标系2下进行投影。步骤如下:
反变换到坐标系1下,就要得到向量基1中的向量在向量基2中的表示方法,然后再在坐标系2下进行投影。步骤如下:
向量基1中x1向量为(1,0),在坐标系2上投影(注意此处投影还是在坐标系1中进行):

![]()
所以向量x1在坐标系2中的坐标为(![]() ,
, ![]() )。
)。
向量基1中y1向量为(0,1),在坐标系2上投影(注意此处投影还是在坐标系1中进行):
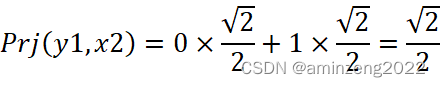
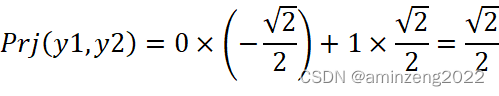
所以向量y1在坐标系2中的坐标为(![]() ,
, ![]() )。
)。
现在坐标系2下,将A=![]() 反变换回坐标系1下:
反变换回坐标系1下:
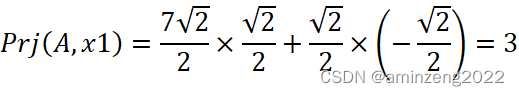
![]()
这就得到了A在坐标系1下的坐标(3,4)。





















 7496
7496











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








