电分糊涂日记之《二阶电路的时域分析》

一、二阶电路的零输入响应分析

我们以电容具有初始值；电感初始值为零的情况分析如下电路
电容的初始状态为 u_C(0₊) = U₀ 电感的初始状态为 i_L(0₊)=0

由KVL、元件VCR,可得到以电容电压为变量的电路微分方程为

换成标准形式【其实就是换成 二阶常系数齐次微分方程】

• 其中 衰减系数为：
  
• RLC串联电路的谐振角频率：
  
  然后求一下特征方程和特征根【这个特征根就是配方-移项求得的】
  

然后就需要讨论 a 与 w₀ 的关系；这个就是看这个电路能不能振荡起来的一个条件；一个有三种情况

• 阻尼电阻：阻尼电阻与电路的动态元件参数、电路结构有关，与电路的激励和初始状态无关。
  

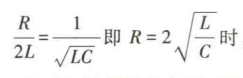
• 1. a > w₀ ：过阻尼
  
  

表明电容一直在释放能量；释放的能量一部分会给电感，电感处于吸收能量状态，即电容释放的能量一部分被电阻消耗，一部分存储于电感；过一段时间后电感储存的能量，电感、电容同时释放的能量均被电阻消耗，最后释放完

• 2. a = w₀ ：临界阻尼
  

波形类似于上图所示波形，仍然无振荡变化过程。然而，这个过程是振荡和非振荡过程的分界线，所以称为临界阻尼过程。

• 1 . a < w₀ ：欠阻尼
  
  
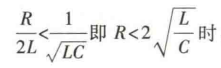
  上所示波形看出，与过阻尼情况不同，欠阻尼情况下，电容电压 u_c(t) 的变化呈衰减振荡趋势，是一个衰减振荡的放电过程。这是由于电阻R值较小，在电容放电(释放能量）的过程中，能量仅被电阻消耗小部分，大量的能量被另一储能元件电感转换为磁场能量储存，当电容储能为零时，电感又开始释放能量，电容被反向充电，又进行电能的储存，如此反复。在电路的动态元件进行周期性的能量交换的过程中，电阻R每次都要消耗一部分能量，使得电容的初始储能在电容与电感周期性的能量交换中被消耗殆尽。
  
  当电路中R=0时，电路初始储能不会被消耗，只会在电容和电感间进行电场储能和磁场储能的不断相互转换，永无休止，成为无阻尼等幅振荡 过程。其响应波形和能量的转换如图所示。
  

经典例题：

二、二阶电路的零状态响应分析

三、二阶电路的全响应