CLASSIFIER-FREE DIFFUSION GUIDANCE

摘要:
分类器引导是最近提出的一种方法,用于在条件扩散模型训练后权衡模式覆盖范围和样本保真度,其理念与其他类型生成模型中的低温采样或截断类似。**分类器引导将扩散模型的得分估计与图像分类器的梯度相结合,因此需要训练一个与扩散模型分开的图像分类器。**这也引发了一个问题,即是否可以在不使用分类器的情况下进行引导。我们表明,确实可以通过纯生成模型在不使用此类分类器的情况下进行引导:在我们所谓的无分类器引导中,我们联合训练一个条件扩散模型和一个无条件扩散模型,并将得到的条件得分估计和无条件得分估计相结合,以实现与使用分类器引导类似的样本质量和多样性之间的权衡。
结论:
我们提出了无分类器引导方法,这是一种在扩散模型中提高样本质量同时降低样本多样性的方法。无分类器引导可以被视为无需分类器的分类器引导,我们展示无分类器引导有效性的结果证实,纯生成扩散模型能够在完全避免分类器梯度的情况下,最大化基于分类器的样本质量指标。我们期待在更多不同的场景和数据模式中对无分类器引导进行进一步探索。
讨论:
我们的无分类器引导方法最实际的优势在于其极其简单:在训练过程中,它只需要对代码进行一行修改——随机丢弃条件信息;在采样过程中,将条件得分估计和无条件得分估计进行混合。相比之下,分类器引导会使训练流程变得复杂,因为它需要额外训练一个分类器。这个分类器必须在加噪的zλz_λzλ上进行训练,因此无法直接使用标准的预训练分类器。
由于无分类器引导能够像分类器引导那样在Inception Score(IS)和Frechet Inception Distance(FID)之间进行权衡,且无需额外训练分类器,我们已经证明可以使用纯生成模型进行引导。此外,我们的扩散模型由无约束的神经网络进行参数化,因此与分类器梯度不同(萨利曼斯和霍,2021年),它们的得分估计不一定形成保守向量场。因此,我们的无分类器引导采样器所遵循的步骤方向与分类器梯度完全不同,因此不能被解释为对分类器的基于梯度的对抗攻击。因此,我们的结果表明,使用纯生成模型,通过一种不利用分类器梯度对图像分类器进行对抗攻击的采样过程,就可以提升基于分类器的IS和FID指标。
我们还对引导机制的工作原理给出了一个直观的解释:它在降低样本的无条件似然的同时增加了条件似然。无分类器引导通过一个负得分项来降低无条件似然,据我们所知,这一点尚未被探索过,并且可能会在其他应用中得到应用。
这里所介绍的无分类器引导依赖于训练一个无条件模型,但在某些情况下可以避免这样做。如果类别分布已知且只有少数几个类别,我们可以利用∑cp(x∣c)p(c)=p(x)∑_c p(x|c)p(c ) = p(x)∑cp(x∣c)p(c)=p(x)这一事实,从条件得分中获取无条件得分,而无需显式地训练无条件得分。当然,这需要对 c 的每个可能值都进行前向传播,并且对于高维条件来说效率会很低。
无分类器引导的一个潜在缺点是采样速度。一般来说,分类器可以比生成模型更小且更快,因此分类器引导采样可能比无分类器引导更快,因为后者需要对扩散模型进行两次前向传播,一次用于条件得分,另一次用于无条件得分。通过改变架构以在网络后期注入条件信息,或许可以缓解运行扩散模型多次传播的必要性,但我们将这一探索留待未来工作。
最后,任何以牺牲多样性为代价来提高样本保真度的引导方法都必须面对一个问题,即多样性的降低是否可以接受。在已部署的模型中可能会产生负面影响,因为在数据的某些部分相对于其他部分代表性不足的应用中,保持样本多样性至关重要。尝试在保持样本多样性的同时提高样本质量,将是未来研究中一个有趣的方向。
介绍:
扩散模型最近作为一类富有表现力且灵活的生成模型崭露头角,在图像和音频合成任务中展现出了具有竞争力的样本质量和似然得分。这些模型在音频合成方面的表现,可与自回归模型相媲美,且推理步骤大幅减。在FID分数和分类准确率方面,它们在ImageNet图像生成任务上的结果优于BigGAN - deep。
分类器引导(classifier guidance)技术利用额外训练的分类器来提升扩散模型的样本质量。在分类器引导技术提出之前,人们尚不清楚如何从扩散模型中生成类似于通过截断BigGAN(Brock等人,2019)或低温Glow(Kingma和Dhariwal,2018)生成的“低温”样本:一些简单的尝试,如缩放模型分数向量或在扩散采样过程中减少添加的高斯噪声量,都是无效的。分类器引导技术则是将扩散模型的分数估计与分类器对数概率的输入梯度相混合。通过改变分类器梯度的强度,分类器引导扩散技术能够以类似于改变BigGAN截断参数的方式,在Inception分数和FID分数(或精确率和召回率)之间进行权衡。
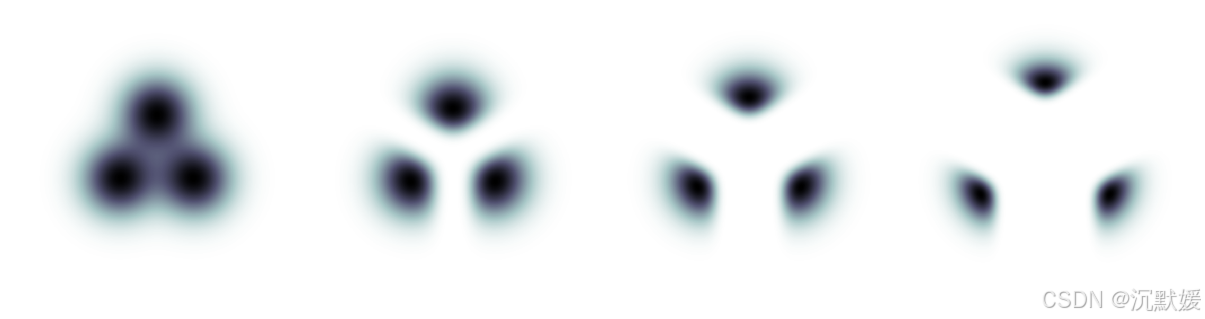
图2:引导(操作)对三个高斯分布混合体产生的影响,每个混合成分代表基于某一类别条件的数据。最左侧的图是非引导的边缘密度。从左到右展示的是在引导强度逐渐增加的情况下,标准化引导条件(分布)混合体的密度。
关心的是能否在不使用分类器的情况下实现分类器引导功能。**分类器引导会使扩散模型的训练流程变得复杂,因为这需要训练一个额外的分类器,并且该分类器必须在含噪数据上进行训练,所以通常无法直接插入一个预训练好的分类器。**此外,由于分类器引导在采样过程中将分数估计与分类器梯度相混合,分类器引导的扩散采样可以被理解为试图用基于梯度的对抗攻击来迷惑图像分类器。这就引发了一个问题:分类器引导之所以能够成功提升基于分类器的指标,如FID(Fréchet Inception距离)和Inception分数(IS),是否仅仅是因为它对这些分类器具有对抗性。沿着分类器梯度的方向进行(调整)也与GAN(生成对抗网络)的训练有一定相似之处,特别是对于非参数生成器而言;这也引发了另一个问题:分类器引导的扩散模型在基于分类器的指标上表现良好,是否是因为它们开始类似于GAN,而众所周知,GAN在这些指标上已经表现出色。
为了解决上述问题,提出了无分类器引导(classifier - free guidance),这是一种完全避免使用任何分类器的引导方法。无分类器引导并非沿着图像分类器的梯度方向进行采样,而是将条件扩散模型和无条件扩散模型(两者联合训练)的分数估计进行混合。通过调整混合权重,我们能够实现与分类器引导类似的FID(Fréchet Inception距离)/IS(Inception分数)权衡。我们的无分类器引导结果表明,纯粹的生成式扩散模型有能力合成出与其他类型生成模型所能生成的、极高保真度的样本。
背景
我们以连续时间的方式训练扩散模型:设 x∼p(x)\mathbf{x} \sim p(\mathbf{x})x∼p(x),且 z={zλ∣λ∈[λmin,λmax]}\mathbf{z} = \{ \mathbf{z}_\lambda \mid \lambda \in [\lambda_{\min}, \lambda_{\max}] \}z={zλ∣λ∈[λmin,λmax]},其中超参数 λmin<λmax∈R\lambda_{\min} < \lambda_{\max} \in \mathbb{R}λmin<λmax∈R,前向过程 q(z∣x)q(\mathbf{z}|\mathbf{x})q(z∣x) 是一个保方差马尔可夫过程(Sohl - Dickstein等人,2015):
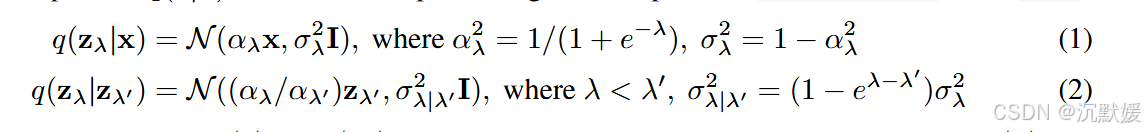
我们将使用符号 p(z)p(\mathbf{z})p(z)(或 p(zλ)p(\mathbf{z}_\lambda)p(zλ))来表示当 x∼p(x)\mathbf{x} \sim p(\mathbf{x})x∼p(x) 且 z∼q(z∣x)\mathbf{z} \sim q(\mathbf{z}|\mathbf{x})z∼q(z∣x) 时,z\mathbf{z}z(或 zλ\mathbf{z}_\lambdazλ)的边缘分布。注意,λ=logαλ2/σλ2\lambda = \log \alpha_\lambda^2 / \sigma_\lambda^2λ=logαλ2/σλ2,所以 λ\lambdaλ 可以解释为 zλ\mathbf{z}_\lambdazλ 的对数信噪比,并且前向过程沿着 λ\lambdaλ 减小的方向进行。

在给定 x\mathbf{x}x 的条件下,前向过程可以通过转移概率 q(zλ′∣zλ,x)=N(μ~λ′∣λ(zλ,x),σ~λ′∣λ2I)q(\mathbf{z}_{\lambda'}|\mathbf{z}_{\lambda}, \mathbf{x}) = \mathcal{N}(\tilde{\mu}_{\lambda'|\lambda}(\mathbf{z}_{\lambda}, \mathbf{x}), \tilde{\sigma}_{\lambda'|\lambda}^2 \mathbf{I})q(zλ′∣zλ,x)=N(μ~λ′∣λ(zλ,x),σ~λ′∣λ2I) 来逆向描述,其中
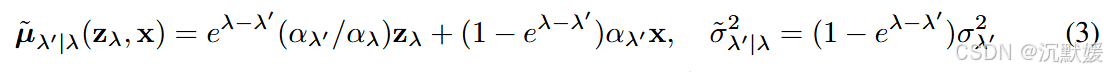
逆向过程生成模型从 pθ(zλmin)=N(0,I)p_{\theta}(\mathbf{z}_{\lambda_{\min}}) = \mathcal{N}(\mathbf{0}, \mathbf{I})pθ(zλmin)=N(0,I) 开始。我们指定转移概率为:
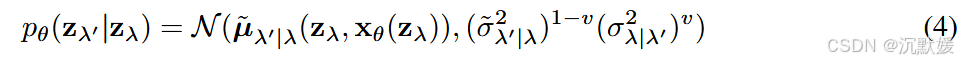
在采样过程中,我们沿着递增序列 λmin=λ1<⋯<λT=λmax\lambda_{\min} = \lambda_1 < \cdots < \lambda_T = \lambda_{\max}λmin=λ1<⋯<λT=λmax 应用此转移过程,进行 TTT 个时间步;换句话说,我们遵循Sohl - Dickstein等人(2015)、Ho等人(2020)的离散时间祖先采样器。如果模型 xθ\mathbf{x}_\thetaxθ 是正确的,那么当 T→∞T \to \inftyT→∞ 时,我们从样本路径分布为 p(z)p(\mathbf{z})p(z) 的随机微分方程(SDE)中获取样本(Song等人,2021b),并且我们用 pθ(z)p_\theta(\mathbf{z})pθ(z) 表示连续时间模型分布。方差是 σ~λ′∣λ2\tilde{\sigma}_{\lambda'|\lambda}^2σ~λ′∣λ2 和 σλ∣λ′2\sigma_{\lambda|\lambda'}^2σλ∣λ′2 的对数空间插值,如Nichol & Dhariwal(2021)所建议;我们发现使用常数超参数 vvv 而非依赖于 zλ\mathbf{z}_\lambdazλ 的学习值 vvv 是有效的。注意,当 λ′→λ\lambda' \to \lambdaλ′→λ 时,方差简化为 σ~λ′∣λ2\tilde{\sigma}_{\lambda'|\lambda}^2σ~λ′∣λ2,因此 vvv 仅在实际中采用非无穷小时间步进行采样时才起作用。
逆向过程的均值来自对 xθ(zλ)≈x\mathbf{x}_\theta(\mathbf{z}_\lambda) \approx \mathbf{x}xθ(zλ)≈x 的估计,该估计被代入 q(zλ′∣zλ,x)q(\mathbf{z}_{\lambda'}|\mathbf{z}_\lambda, \mathbf{x})q(zλ′∣zλ,x)(Ho等人,2020;Kingma等人,2021)(xθ\mathbf{x}_\thetaxθ 也将 λ\lambdaλ 作为输入,但为使符号简洁,我们省略了它)。我们用 ϵ\epsilonϵ - 预测来参数化 xθ\mathbf{x}_\thetaxθ(Ho等人,2020):xθ(zλ)=(zλ−σλϵθ(zλ))/αλ\mathbf{x}_\theta(\mathbf{z}_\lambda) = (\mathbf{z}_\lambda - \sigma_\lambda \epsilon_\theta(\mathbf{z}_\lambda)) / \alpha_\lambdaxθ(zλ)=(zλ−σλϵθ(zλ))/αλ,并在以下目标函数上进行训练:

其中 ϵ∼N(0,I)\boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})ϵ∼N(0,I),zλ=αλx+σλϵ\mathbf{z}_\lambda = \alpha_\lambda \mathbf{x} + \sigma_\lambda \boldsymbol{\epsilon}zλ=αλx+σλϵ,且 λ\lambdaλ 是从 [λmin,λmax][\lambda_{\min}, \lambda_{\max}][λmin,λmax] 上的分布 p(λ)p(\lambda)p(λ) 中抽取的。该目标函数是对多个噪声尺度下的去噪分数匹配(Vincent,2011;Hyvärinen & Dayan,2005)(Song & Ermon,2019),当 p(λ)p(\lambda)p(λ) 为均匀分布时,该目标函数与潜在变量模型的边际对数似然的变分下界成正比 ∫pθ(x∣z)pθ(z)dz\int p_\theta(\mathbf{x}|\mathbf{z}) p_\theta(\mathbf{z}) d\mathbf{z}∫pθ(x∣z)pθ(z)dz,忽略了未指定解码器 pθ(x∣z)p_\theta(\mathbf{x}|\mathbf{z})pθ(x∣z) 和 zλmin\mathbf{z}_{\lambda_{\min}}zλmin 处先验的项(Kingma等人,2021)。
如果 p(λ)p(\lambda)p(λ) 不是均匀分布,该目标函数可以解释为加权变分下界,其权重可以根据样本质量进行调整(Ho等人,2020;Kingma等人,2021)。我们使用受Nichol & Dhariwal(2021)的离散时间余弦噪声调度启发的 p(λ)p(\lambda)p(λ):我们通过 λ=−2logtan(au+b)\lambda = -2 \log \tan(a u + b)λ=−2logtan(au+b) 对均匀分布的 u∈[0,1]u \in [0, 1]u∈[0,1] 进行采样,其中 b=arctan(e−λmax/2)b = \arctan(e^{-\lambda_{\max}/2})b=arctan(e−λmax/2) 且 a=arctan(e−λmin/2)−ba = \arctan(e^{-\lambda_{\min}/2}) - ba=arctan(e−λmin/2)−b。这表示一种修改后的双曲正割分布,以在有界区间上得到支持。对于有限时间步生成,我们使用对应于均匀间隔 u∈[0,1]u \in [0, 1]u∈[0,1] 的 λ\lambdaλ 值,最终生成的样本为 xθ(zλmax)\mathbf{x}_\theta(\mathbf{z}_{\lambda_{\max}})xθ(zλmax)。
因为 ϵθ(zλ)\boldsymbol{\epsilon}_\theta(\mathbf{z}_\lambda)ϵθ(zλ) 的损失函数是所有 λ\lambdaλ 的去噪分数匹配,我们的模型学习到的分数 ϵθ(zλ)\boldsymbol{\epsilon}_\theta(\mathbf{z}_\lambda)ϵθ(zλ) 估计了带噪数据 zλ\mathbf{z}_\lambdazλ 分布的对数密度的梯度,即 ϵθ(zλ)≈−σλ∇zλlogp(zλ)\boldsymbol{\epsilon}_\theta(\mathbf{z}_\lambda) \approx - \sigma_\lambda \nabla_{\mathbf{z}_\lambda} \log p(\mathbf{z}_\lambda)ϵθ(zλ)≈−σλ∇zλlogp(zλ);然而,请注意,由于我们使用无约束神经网络来定义 ϵθ\boldsymbol{\epsilon}_\thetaϵθ,可能不存在梯度为 ϵθ\boldsymbol{\epsilon}_\thetaϵθ 的标量势函数。从学习到的扩散模型中进行采样类似于使用朗之万扩散从收敛到原始数据 x\mathbf{x}x 的条件分布 p(x)p(\mathbf{x})p(x) 的分布序列 p(zλ)p(\mathbf{z}_\lambda)p(zλ) 中进行采样。
在条件生成建模的情况下,数据 x\mathbf{x}x 与条件信息 c\mathbf{c}c(即用于类条件图像生成的类标签)联合绘制。对该模型的唯一修改是逆向过程函数近似器接收 c\mathbf{c}c 作为输入,如 ϵθ(zλ,c)\boldsymbol{\epsilon}_\theta(\mathbf{z}_\lambda, \mathbf{c})ϵθ(zλ,c)。

引导
某些生成模型(如生成对抗网络(GANs)和基于流的模型)一个有趣的特性是,通过在采样时降低生成模型输入噪声的方差或范围,能够执行截断采样或低温采样。其预期效果是降低样本的多样性,同时提高每个单独样本的质量。例如,在BigGAN(Brock等人,2019)中,截断分别在低截断量和高截断量下产生FID分数和Inception分数之间的权衡曲线。Glow(Kingma & Dhariwal,2018)中的低温采样也有类似效果。
不幸的是,在扩散模型中实现截断或低温采样的直接尝试是无效的。例如,缩放模型分数或在逆向过程中降低高斯噪声的方差,会导致扩散模型生成模糊、低质量的样本(Dhariwal & Nichol,2021)。
3.1 分类器引导
为了在扩散模型中获得类似截断的效果,Dhariwal & Nichol(2021)引入了分类器引导(classifier guidance),其中扩散分数(score)θ(zλ,c)≈−σλ∇zλlogp(zλ∣c)\theta(\mathbf{z}_\lambda, \mathbf{c}) \approx - \sigma_\lambda \nabla_{\mathbf{z}_\lambda} \log p(\mathbf{z}_\lambda|\mathbf{c})θ(zλ,c)≈−σλ∇zλlogp(zλ∣c) 被修改为包含辅助分类器模型 pθ(c∣zλ)p_\theta(\mathbf{c}|\mathbf{z}_\lambda)pθ(c∣zλ) 的对数似然梯度,具体如下:
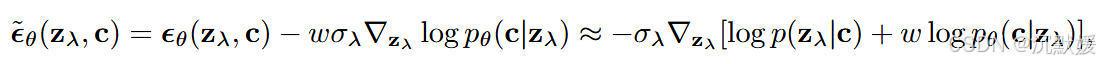
其中 www 是一个控制分类器引导强度的参数。在从扩散模型中采样时,这个修改后的分数 ϵ~θ(zλ,c)\tilde{\epsilon}_\theta(\mathbf{z}_\lambda, \mathbf{c})ϵ~θ(zλ,c) 代替 ϵθ(zλ,c)\epsilon_\theta(\mathbf{z}_\lambda, \mathbf{c})ϵθ(zλ,c) 被使用,从而从分布 p~θ(zλ∣c)∝pθ(zλ∣c)pθ(c∣zλ)w\tilde{p}_\theta(\mathbf{z}_\lambda|\mathbf{c}) \propto p_\theta(\mathbf{z}_\lambda|\mathbf{c}) p_\theta(\mathbf{c}|\mathbf{z}_\lambda)^wp~θ(zλ∣c)∝pθ(zλ∣c)pθ(c∣zλ)w 中得到近似样本。
其效果是提高了分类器 pθ(c∣zλ)p_\theta(\mathbf{c}|\mathbf{z}_\lambda)pθ(c∣zλ) 为正确标签赋予高似然概率的数据的概率:分类效果好的数据在感知质量的Inception分数上会得到高分(Salimans等人,2016),这从设计上奖励了生成模型。因此,Dhariwal和Nichol发现,通过设置 w>0w > 0w>0,他们可以提高扩散模型的Inception分数,但代价是样本的多样性降低。
图2展示了在三类玩具2D示例上数值求解的引导 p~θ(zλ∣c)∝pθ(zλ∣c)pθ(c∣zλ)w\tilde{p}_\theta(\mathbf{z}_\lambda|\mathbf{c}) \propto p_\theta(\mathbf{z}_\lambda|\mathbf{c}) p_\theta(\mathbf{c}|\mathbf{z}_\lambda)^wp~θ(zλ∣c)∝pθ(zλ∣c)pθ(c∣zλ)w 的效果,其中每类的条件分布是各向同性高斯分布。应用引导后,每个条件的形式明显是非高斯的。随着引导强度的增加,每个条件将概率质量放置在离其他类别更远、朝向逻辑回归给出的高置信度方向的位置,并且大部分质量集中在更小的区域。这种行为可以看作是在ImageNet模型中增加分类器引导强度时出现的Inception分数提升和样本多样性降低的简单表现。
理论上,对无条件模型应用权重为 w+1w + 1w+1 的分类器引导,与对条件模型应用权重为 www 的分类器引导会得到相同的结果,因为 pθ(zλ∣c)pθ(c∣zλ)w∝pθ(zλ)pθ(c∣zλ)w+1p_\theta(\mathbf{z}_\lambda|\mathbf{c}) p_\theta(\mathbf{c}|\mathbf{z}_\lambda)^w \propto p_\theta(\mathbf{z}_\lambda) p_\theta(\mathbf{c}|\mathbf{z}_\lambda)^{w + 1}pθ(zλ∣c)pθ(c∣zλ)w∝pθ(zλ)pθ(c∣zλ)w+1;或者用分数表示:
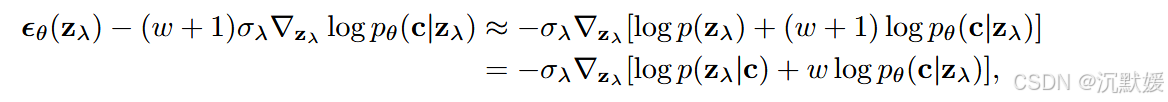
但有趣的是,Dhariwal和Nichol在对已经以类为条件的模型应用分类器引导时获得了最佳结果,而不是对无条件模型应用引导。因此,我们将保持在引导已经以类为条件的模型的设置中。

3.2 无分类器引导
虽然分类器引导如同在截断或低温采样中所预期的那样,成功地在Inception分数(IS)和Fréchet Inception距离(FID)之间进行权衡,但它仍然依赖于图像分类器的梯度。出于第1节所述的原因,我们试图消除分类器。在此,我们描述无分类器引导,它在无需此类梯度的情况下实现相同的效果。无分类器引导是一种修改 ϵθ(zλ,c)\epsilon_\theta(\mathbf{z}_\lambda, \mathbf{c})ϵθ(zλ,c) 以获得与分类器引导相同效果,但无需分类器的替代方法。算法1和算法2详细描述了使用无分类器引导进行训练和采样的过程。
我们没有训练单独的分类器模型,而是选择训练一个无条件的去噪扩散模型 pθ(z)p_\theta(\mathbf{z})pθ(z),该模型通过分数估计器 ϵθ(zλ)\epsilon_\theta(\mathbf{z}_\lambda)ϵθ(zλ) 进行参数化,同时训练一个有条件的模型 pθ(z∣c)p_\theta(\mathbf{z}|\mathbf{c})pθ(z∣c),该模型通过 ϵθ(zλ,c)\epsilon_\theta(\mathbf{z}_\lambda, \mathbf{c})ϵθ(zλ,c) 进行参数化。我们使用单个神经网络对这两个模型进行参数化,对于无条件模型,在预测分数时,我们可以简单地将类标识符 c\mathbf{c}c 输入为空标记 ∅\emptyset∅,即 ϵθ(zλ)=ϵθ(zλ,c=∅)\epsilon_\theta(\mathbf{z}_\lambda) = \epsilon_\theta(\mathbf{z}_\lambda, \mathbf{c} = \emptyset)ϵθ(zλ)=ϵθ(zλ,c=∅)。我们通过以一定的概率 puncondp_{\text{uncond}}puncond(作为超参数设置)将 c\mathbf{c}c 随机设置为无条件类标识符 ∅\emptyset∅,来联合训练无条件和有条件模型。(当然,也可以训练单独的模型,而不是将它们联合训练,但我们选择联合训练,因为它实现起来非常简单,不会使训练流程复杂化,也不会增加参数的总数。)然后,我们使用有条件和无条件分数估计的以下线性组合进行采样:
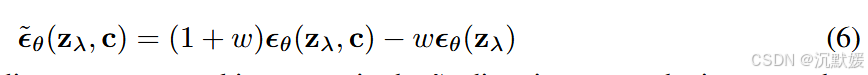
公式(6)中没有分类器梯度,因此,沿着 ϵ~θ\tilde{\boldsymbol{\epsilon}}_\thetaϵ~θ 方向迈出的一步不能被解释为对图像分类器的基于梯度的对抗攻击。此外,由于使用了无约束神经网络,ϵ~θ\tilde{\boldsymbol{\epsilon}}_\thetaϵ~θ 是由非保守向量场的分数估计构建的,所以通常不存在一个标量势(如分类器对数似然),使得 ϵ~θ\tilde{\boldsymbol{\epsilon}}_\thetaϵ~θ 是分类器引导的分数。
尽管通常可能不存在一个分类器,使得公式(6)是分类器引导的分数,但它实际上受到了隐式分类器 pi(c∣zλ)∝p(zλ∣c)/p(zλ)p^i(\mathbf{c}|\mathbf{z}_\lambda) \propto p(\mathbf{z}_\lambda|\mathbf{c}) / p(\mathbf{z}_\lambda)pi(c∣zλ)∝p(zλ∣c)/p(zλ) 梯度的启发。如果我们能得到精确的分数 ϵ∗(zλ,c)\boldsymbol{\epsilon}^*(\mathbf{z}_\lambda, \mathbf{c})ϵ∗(zλ,c) 和 ϵ∗(zλ)\boldsymbol{\epsilon}^*(\mathbf{z}_\lambda)ϵ∗(zλ)(分别对应 p(zλ∣c)p(\mathbf{z}_\lambda|\mathbf{c})p(zλ∣c) 和 p(zλ)p(\mathbf{z}_\lambda)p(zλ)),那么这个隐式分类器的梯度将是 ∇zλlogpi(c∣zλ)=−1σλ[ϵ∗(zλ,c)−ϵ∗(zλ)]\nabla_{\mathbf{z}_\lambda} \log p^i(\mathbf{c}|\mathbf{z}_\lambda) = - \frac{1}{\sigma_\lambda} [\boldsymbol{\epsilon}^*(\mathbf{z}_\lambda, \mathbf{c}) - \boldsymbol{\epsilon}^*(\mathbf{z}_\lambda)]∇zλlogpi(c∣zλ)=−σλ1[ϵ∗(zλ,c)−ϵ∗(zλ)],并且使用这个隐式分类器的分类器引导会将分数估计修改为 ϵ~∗(zλ,c)=(1+w)ϵ∗(zλ,c)−wϵ∗(zλ)\tilde{\boldsymbol{\epsilon}}^*(\mathbf{z}_\lambda, \mathbf{c}) = (1 + w) \boldsymbol{\epsilon}^*(\mathbf{z}_\lambda, \mathbf{c}) - w \boldsymbol{\epsilon}^*(\mathbf{z}_\lambda)ϵ~∗(zλ,c)=(1+w)ϵ∗(zλ,c)−wϵ∗(zλ)。注意这与公式(6)的相似性,但也要注意 ϵ~∗(zλ,c)\tilde{\boldsymbol{\epsilon}}^*(\mathbf{z}_\lambda, \mathbf{c})ϵ~∗(zλ,c) 与 ϵ~θ(zλ,c)\tilde{\boldsymbol{\epsilon}}_\theta(\mathbf{z}_\lambda, \mathbf{c})ϵ~θ(zλ,c) 有根本不同。前者是由缩放后的分类器梯度 ϵ∗(zλ,c)−ϵ∗(zλ)\boldsymbol{\epsilon}^*(\mathbf{z}_\lambda, \mathbf{c}) - \boldsymbol{\epsilon}^*(\mathbf{z}_\lambda)ϵ∗(zλ,c)−ϵ∗(zλ) 构建的;后者是由估计值 ϵθ(zλ,c)−ϵθ(zλ)\boldsymbol{\epsilon}_\theta(\mathbf{z}_\lambda, \mathbf{c}) - \boldsymbol{\epsilon}_\theta(\mathbf{z}_\lambda)ϵθ(zλ,c)−ϵθ(zλ) 构建的,并且这个表达式通常不是(缩放后的)任何分类器的梯度,同样是因为分数估计是无约束神经网络的输出。
事先并不明显的是,使用贝叶斯规则反转生成模型会产生一个能提供有用引导信号的良好分类器。例如,Grandvalet & Bengio(2004)发现,判别模型通常优于从生成模型推导出的隐式分类器,即使在生成模型的设定与数据分布完全匹配的人工情况下也是如此。在我们预期模型会被错误设定的情况下,由贝叶斯规则推导出的分类器可能不一致(Grünwald & Langford,2007),并且我们对它们的性能没有任何保证。然而,在第4节中,我们通过实验表明,无分类器引导能够以与分类器引导相同的方式在FID和IS之间进行权衡。在第5节中,我们讨论了无分类器引导相对于分类器引导的影响。
 无分类器引导:提升扩散模型质量
无分类器引导:提升扩散模型质量


























 5336
5336

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










