（2024，Infini-T，Infini-A，压缩记忆，长期记忆）使用无限注意力的高效无限上下文 Transformer

EDPJ，公众号（EDPJ）

已于 2024-04-13 10:51:30 修改

阅读量1.9k

点赞数 11

分类专栏：论文笔记文章标签： transformer 深度学习人工智能

于 2024-04-13 10:45:30 首次发布

本文链接：https://blog.csdn.net/qq_44681809/article/details/137697269

版权

论文笔记专栏收录该内容

356 篇文章

订阅专栏

Leave No Context Behind: Efficient Infinite Context Transformers with Infini-attention

公和众和号：EDPJ（进 Q 交流群：922230617 或加 VX：CV_EDPJ 进 V 交流群）

Google 在上一篇对 Transformer 的改进的文章中通过对 token 的 “选择” 来减少计算量。而 “选择” 也是 Mamba 中至关重要的一环。

（2024，FLOPs 动态分配，MoD，MoDE，top-k 路由，块丢弃）在基于 Transformer 的语言模型中动态分配计算

（2023，SSM，门控 MLP，选择性输入，上下文压缩）Mamba：具有选择性状态空间的线性时间序列建模_选择性状态空间序列模型

而在本文中，类似于 SSM 和 Mamba，使用 RNN 来为 Transformer 引入长期记忆。此外，它通过复用（reuse）点积注意力计算中的 query、key 和 value 状态（Q、K 和 V），来实现记忆压缩。

0. 摘要

这项工作介绍了一种有效的方法，可以将基于 Transformer 的大型语言模型（LLM）扩展到无限长的输入，并限制内存和计算。我们提出的方法的一个关键组成部分是一种称为无限注意力（Infini-attention）的新型注意力技术。无限注意力将一个压缩式记忆（compressive memory）引入到基本的注意力机制中，并在单个 Transformer 块中构建了掩蔽的局部注意力和长期线性注意力机制。我们在长上下文语言建模基准测试、1M 序列长度的关键上下文块检索和 500K 长度的书籍摘要任务上展示了我们方法的有效性，其中包括了 1B 和 8B 的 LLM。我们的方法引入了最小限制的内存参数，并为 LLM 提供了快速的流式推理（streaming inference）。

2. 方法

图 2 比较了我们的模型 Infini-Transformer 和 Transformer-XL（Dai 等，2019）。与 Transformer-XL 相似，Infini-Transformer 在一个片段序列上操作。我们在每个片段内计算标准的因果点积注意力上下文。因此，点积注意力的计算在某种意义上是局部的，它涵盖了当前段的总 N 个标记的索引 S（N 是段的长度）。

然而，局部注意力（Dai 等，2019）在处理下一个片段时会丢弃前一个片段的注意力状态。在 Infini-Transformers 中，我们提议重新使用旧的 KV 注意力状态，以使用压缩记忆保留完整上下文历史。因此，Infini-Transformers 的每个注意力层都具有全局压缩和局部细粒度状态。我们将这样一个高效的注意力机制称为 Infini-attention，如图 1 所示。

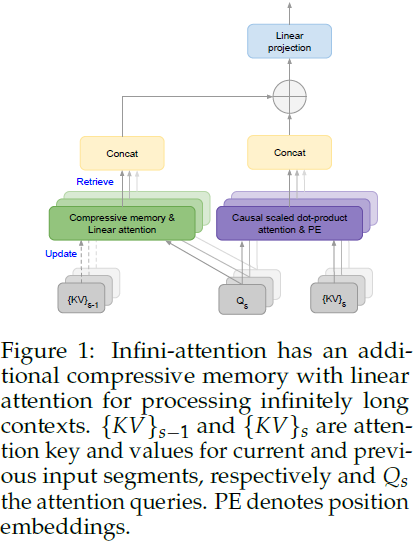
2.1 Infini-attention

如图 1 所示，我们的 Infini-attention 计算局部和全局上下文状态，并将它们组合为其输出。类似于多头注意力（multi-head attention，MHA），除了点积注意力，它还在每个注意力层保留 H 个并行的压缩记忆（H 是注意力头的数量）。

2.1.1 扩展的点积注意力

多头扩展点积注意力（multi-head scaled dot-product attention）（Vaswani等，2017），特别是其自注意力变体（Munkhdalai 等，2016；Cheng等，2016），一直是 LLM 中的主要构建模块。MHA 在建模上下文相关的动态计算方面具有很强的能力，并且在自回归生成模型中广泛利用了其时间掩码（temporal masking）的便利性。

在普通 MHA 中，单个头从输入片段序列 X∈ R^(N × d_model) 计算其注意力上下文 A_dot ∈ R^(N × d_value) 如下。首先，它计算注意力 query、key 和 value 状态：

其中，W_K ∈ R^(d_model × d_key)，W_V ∈ R^(d_model × d_value)，W_Q ∈ R^(d_model × d_key) 是可训练的投影矩阵。然后，注意力上下文被计算为所有其他值的加权平均值。

对于 MHA，我们并行计算每个序列元素的 H 个注意力上下文向量，沿第二维将它们连接起来，然后最终将连接的向量投影到模型空间以获得注意力输出。

2.1.2 压缩记忆

在 Infini-attention 中，我们不是为压缩记忆计算新的记忆条目，而是复用（reuse）点积注意力计算中的 query、key 和 value 状态（Q、K 和 V）。点积注意力和压缩记忆之间的状态共享和复用不仅能够实现高效的插入式长上下文适应，还能加速训练和推理过程。与先前的工作类似（Munkhdalai 等，2019），我们的目标是在压缩记忆中存储 key 和 value 状态的绑定（bindings），并使用 query 向量检索。

虽然文献中提出了不同形式的压缩记忆（Hopfield，1982；Kanerva，1988；Schlag等，2019；Munkhdalai等，2019），但为了简单和计算效率，在这项工作中，我们使用关联矩阵（associative matrix）来参数化记忆（Schlag等，2020）。这种方法进一步使我们能够将记忆更新和检索过程转化为线性注意力机制（Shen等，2018），并利用相关方法中的稳定训练技术。特别地，我们采用了 Katharopoulos 等人（2020）提出的更新规则和检索机制，主要是因为其简单性和竞争性能表现。

记忆检索。在 Infini-attention 中，我们通过使用 query Q∈ R^(N × d_key) 从记忆 M_(s−1) ∈ R^(d_key × d_value) 中检索新内容 A_mem ∈ R^(N × d_key)：

其中，σ 和 z_(s−1) ∈ R^(d_key) 分别是非线性激活函数和归一化项。由于非线性和归一化方法的选择对于训练稳定性至关重要，我们按照 Katharopoulos 等人（2020）的方法，将所有 key 的总和记录为归一化项 z_(s−1)，并使用元素级 ELU + 1 作为激活函数（Clevert等，2015）。
记忆更新。一旦检索完成，我们使用新的 KV 条目更新记忆和归一化项，并获得下一个状态：

然后，新的记忆状态 Ms 和 zs 传递到下一个片段 S + 1 中，在每个注意力层中建立循环。方程（4）中的右侧项 σ(K)^T·V 被称为关联绑定运算符(（associative binding operator）（Smolensky，1990；Hebb，2005；Schlag等，2020）。

受到增量规则（delta rule）（Munkhdalai等，2019；Schlag等，2020；2021）的启发，我们将其纳入了我们的 Infini-attention 中。通过检索现有的 value 条目并在应用关联绑定作为新更新之前从新 value 中减去它们，增量规则尝试稍微改进记忆更新。

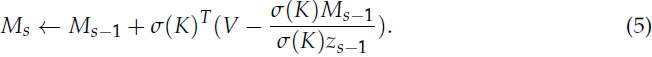
这个更新规则（线性+增量）在记忆中保持关联矩阵不变，如果 KV 绑定已经存在于记忆中，则仍然跟踪与前一个（线性）相同的归一化项，以确保数值稳定性。

长期上下文注入。我们通过一个学习得到的门控标量 β 将局部注意力状态 A_dot 和记忆检索的内容 A_mem 聚合起来：

这只添加了一个标量值作为每个头的训练参数，同时允许模型中长期和局部信息流之间的可学习权衡（Wu等，2022）。类似于标准 MHA，对于多头 Infini-attention，我们并行计算 H 个上下文状态，并将它们连接和投影为最终的注意力输出 O ∈ R^(N × d_model)：

其中，W_O ∈ R^(H × d_value × d_model) 是可训练的权重。

2.2 记忆和有效上下文窗口

我们的 Infini-Transformer 能够在有限内存占用的情况下实现无限上下文窗口。为了说明这一点，表 1 列出了先前的段级记忆模型及其上下文-内存占用和以模型参数和输入段长度定义的有效上下文长度。Infini-Transformer 在单层每个头中存储压缩上下文的内存复杂度为 d_key × d_value + d_key，而对于其他模型，复杂度随着序列维度的增加而增加——内存复杂度取决于 Transformer-XL（Dai等，2019）、Compressive Transformer（Rae等，2019）和 Memorizing Transformer（Wu等，2022）的缓存大小或者 RTM（Bulatov等，2022）和 AutoCompressors（Ge等，2023）的软提示大小。

除了当前状态，Transformer-XL 还计算对上一段缓存的 KV 状态的注意力。由于这是每一层都要做的，Transformer-XL 将上下文窗口从 N 扩展到 N×l 个 token，并额外增加了 (d_key + d_value) × H × N × l 的内存占用。
压缩 Transformer 在 Transformer-XL 的基础上添加了第二个缓存，并存储了上一段的激活的压缩表示。因此，它将 Transformer-XL 的上下文窗口扩展了 c×r×l，但仍然具有较大的上下文-内存复杂度。
进一步发展这个想法，记忆 Transformer 选择将整个 KV 状态作为输入序列的上下文进行存储。由于在这种情况下存储成本变得过高，它们将上下文计算限制为仅在单个层中进行。通过利用快速 kNN 检索器，记忆 Transformer 构建一个覆盖长度为 N×S 的完整序列历史的上下文窗口，但存储成本增加。
我们的实验表明，Infini-Transformer LM 在记忆 Transformer 的基础上可以实现超过 100 倍的压缩率，同时进一步改善了困惑度得分。

RMT 和 AutoCompressors 允许无限的上下文长度，因为它们将输入压缩为摘要向量，然后将它们作为额外的软提示输入传递给后续的段。然而，在实践中，这些技术的成功高度取决于软提示向量的大小。换句话说，必须增加软提示（摘要）向量的数量才能通过 AutoCompressors 实现更好的性能（Chevalier等，2023），而随之而来的是内存和计算复杂度快速增长，导致效率降低。在AutoCompressors（Chevalier等，2023）中也观察到需要一个高效的压缩目标来训练这种提示压缩技术（Ge等，2023）。

3. 实验

我们在涉及极长输入序列的基准测试上评估了我们的 Infini-Transformer 模型：长上下文语言建模、100 万长度的关键上下文块检索和 50 万长度的书籍摘要任务。对于语言建模基准测试，我们从头开始训练我们的模型，而对于关键上下文块检索和书籍摘要任务，我们持续预训练现有的LLMs，以突出我们方法的插入式长上下文适应能力。

门控分数可视化。图 3 展示了每层中所有注意力头部的压缩记忆的门控分数，即 sigmoid(β)。在训练后，Infini-attention 中出现了两种类型的头部：具有接近 0 或 1 的门控分数的专门头部，以及得分接近 0.5 的混合头部。专门头部通过局部注意力计算处理上下文信息或从压缩记忆中检索，而混合头部将当前上下文信息和长期记忆内容聚合到单个输出中。有趣的是，每一层至少都有一个短距离头部，允许输入信号向前传播直至输出层。我们还观察到在前向计算过程中长期和短期内容检索的交错。

4. 相关工作

压缩记忆（Compressive memory）。受生物神经元中的可塑性启发（Munkhdalai＆Yu，2017a；Miconi等，2018），压缩记忆方法将参数化函数视为储存和检索信息的记忆（Hinton＆Plaut，1987；Schmidhuber，1992；Ba等，2016；Munkhdalai等，2019）。与 Transformer KV 内存阵列（Vaswani等，2017；Wu等，2022）不同，后者随着输入序列长度增加而增长，压缩记忆系统为了计算效率而保持恒定数量的内存参数。这些参数通过更新规则进行修改以存储信息，然后通过内存读取机制进行检索（Graves等，2014；Sukhbaatar等，2015；Munkhdalai＆Yu，2017b）。

压缩的输入表示可以视为过去序列片段的摘要（Rae等，2019；Chevalier等，2023）。沿着这个方向，更近期的工作已经开始利用 Transformer LLM 本身来压缩输入序列以进行高效的长上下文建模（Bulatov等，2022；Chevalier等，2023；Ge等，2023；Mu等，2024）。然而，之前的段级压缩方法，包括压缩 Transformer （Rae等，2019），仍然丢弃了旧段的记忆条目，以便为新的段释放空间，从而将其上下文窗口限制在最近的段。这与我们的 Infini-attention 形成对比，后者以递归的方式计算到固定数量的内存参数的增量记忆更新。

长上下文连续预训练。有一系列的工作延伸了点积注意力层，并继续为长上下文训练 LLMs（Xiong等，2023；Fu等，2024）。注意力扩展包括将稀疏性纳入注意力层（Chen等，2023b；Ratner等，2022；Mohtashami＆Jaggi，2024），以及操作位置编码（Chen等，2023a；Peng等，2023）。尽管基于位置编码的方法，如位置插值技术（Chen等，2023a），在数据效率上可能是有效的，因为它们只调整注意力层中的位置偏置，但对推理来说仍然昂贵。

注意力机制也容易受到注意力漏斗（attention sink）（Xiao等，2023）和中间丢失（lost-in-the-middle）（Liu等，2024）等问题的影响。因此，它们在上下文长度超过训练过程中观察到的长度时往往难以应对（Press等，2021；Kazemnejad等，2024）。

Infini-attention 通过在长序列上进行段级流式计算并采用固定的局部注意力窗口，解决了这些问题。我们的 Infini-Transformers 在训练 32K 甚至 5K 长度序列时成功推广到 100 万输入长度范围。

高效的注意力。高效的注意力技术试图通过近似或系统级优化来提高点积注意力的效率。针对不同形式的高效注意力近似已经探索了多种方向，包括基于稀疏性的（Child等，2019；Beltagy等，2020；Sukhbaatar等，2021；Ding等，2023）和线性注意力近似（Shen等，2018；Katharopoulos等，2020；Schlag等，2021）。在这些中，线性注意力变体与关联记忆矩阵（Schlag等，2020；2021）和元学习神经记忆（Munkhdalai等，2019）密切相关，其中 KV 绑定（Smolensky，1990）存储在快速权重中（Hinton＆Plaut，1987；Schmidhuber，1992；Ba等，2016），这些权重根据新的上下文信息进行修改。最近，通过利用特定硬件架构提出了系统级优化技术，以使确切的注意力计算更加高效（Dao等，2022；Liu等，2023）。

5. 结论

一个有效的记忆系统不仅对于理解 LLM 中的长上下文至关重要，而且对于推理、规划、持续适应新知识，甚至学习如何学习也是至关重要的。本研究将压缩记忆模块与普通点积注意力层紧密集成。这种微妙但关键的注意力层修改使得 LLM 能够在有限的内存和计算资源下处理无限长的上下文。我们展示了我们的方法可以自然地扩展到输入序列长度为百万级别，同时在长上下文语言建模基准和书籍摘要任务上优于基线。我们还展示了我们方法的良好长度泛化能力。对于训练了 5K 序列长度的 1B 模型，其能够解决 1M 长度问题。