（2022，扩散模型，评分函数，数据流形的内在维度，SVD）使用扩散模型估计数据流形的维度

Your diffusion model secretly knows the dimension of the data manifold

公和众和号：EDPJ（进 Q 交流群：922230617 或加 VX：CV_EDPJ 进 V 交流群）

目录

0. 摘要

1. 引言

2. 相关工作

3. 背景：基于评分的扩散模型

4. 提出的方法：内在维度（Intrinsic Dimension）估计

6. 局限性

7. 实验

8. 结论及进一步方向

---

0. 摘要

在这项工作中，我们提出了一种使用训练好的扩散模型来估计数据流形维度的新框架。扩散模型逼近评分函数，即目标分布的噪声污染版本在不同污染水平下的对数密度梯度。我们证明，如果数据集中在嵌入高维环境空间的流形周围，那么随着污染水平的降低，评分函数会指向流形，因为这个方向成为了最大可能性增加的方向。因此，对于较小的污染水平，扩散模型为我们提供了对数据流形法向束（normal bundle）的近似。这使我们能够估计切向空间（tangent space）的维度，即数据流形的内在维度（Intrinsic Dimension）。据我们所知，我们的方法是第一个基于扩散模型的数据流形维度估计器，并且在对欧几里得数据和图像数据进行的控制实验中，它的性能优于已建立的统计估计器。 

（2024，扩散，去噪调度，维度，误差，收敛速度）适应基于分数的扩散模型中的未知低维结构

1. 引言

许多现代实际数据集包含大量变量，通常超过观测数量。这在建模时带来了重大挑战，因为维度灾难。然而，尽管存在这种复杂性，这类数据通常集中在一个低维流形周围，这一概念被称为流形假设【Fefferman 等，2013】。这一假设指导了现代高维数据建模技术的发展，如 GAN 【Goodfellow 等，2014】和 VAE【Kingma 和 Welling，2013】，以及降维方法，如 PCA【Pearson，1901】和 t-SNE【Hinton 和 Roweis，2002】。这些方法需要了解数据的内在维度，这是一个关键的超参数。

在这项工作中，我们介绍了一种新方法，通过利用训练好的扩散模型中的信息来估计数据流形的维度。

扩散模型【Sohl-Dickstein 等，2015；Ho 等，2020a】是一类新的深度生成模型，能够在不需要事先了解数据内在维度的情况下捕捉复杂的高维分布。我们展示了尽管这些模型不显式依赖数据的内在维度，但它们隐含地估计了数据的内在维度。

如【Song 等，2020；Ho 等，2020a】所示，扩散模型执行分数匹配【Hyvärinen，2005】，因此包含了数据分布对数密度梯度的信息。我们的方法利用了一个见解：在数据流形附近，对数密度的梯度是与流形本身正交的。这一关键观察为推断流形的维度提供了工具。

我们在已知数据流形维度的合成欧几里得数据（synthetic Euclidean）和图像数据集上评估了该方法的性能。此外，我们将该方法应用于 MNIST 数据集【LeCun 和 Cortes，2010】（其内在维度未知），并通过训练具有不同潜在维度的自编码器的重建误差评估其性能。

2. 相关工作

估计内在维度的问题已被广泛研究。主要有两条研究路线：基于 PCA 的方法和基于最近邻的方法。

PCA。

• 在早期工作中【Fukunaga 和 Olsen，1971】，作者提出了一种基于局部 Karhunen–Loève 展开的方法。
• 在随后的几年中，许多基于PCA的方法被开发出来。
• 最值得注意的是，在【Minka，2000】中，作者提出了一种基于概率 PCA（PPCA）框架的内在维度估计器【Bishop 和 Tipping，2001】。
• 在【Fan 等，2010】中，提出了一种局部 PCA 方法。

最近邻。

• 在【Pettis 等，1979】中，作者提出了一种基于最近邻信息的估计器。
• 在【Levina 和 Bickel，2004】中，作者介绍了一种基于与 m 个最近邻距离的最大似然（MLE）方法。他们的方法在【Haro 等，2008】的工作中得到了进一步改进。

其他。

• 最近，Pope 等【2021】将 MLE 方法应用于估计现代图像数据集（如 MNIST【LeCun 和 Cortes，2010】、CIFAR【Krizhevsky，2012】和 ImageNet【Deng 等，2009】）的内在维度。
• 其他工作则探索了使用基于分形的方法【Camastra 和 Vinciarelli，2002】或填充数（packing numbers）【Kégl，2002】的几何方法。

据我们所知，我们是第一个提出使用扩散模型近似数据流形内在维度的方法。

3. 背景：基于评分的扩散模型

在【Song 等，2020】中，基于分数的生成模型【Hyvärinen，2005】和基于扩散的生成模型【Sohl-Dickstein 等，2015；Ho 等，2020a】被统一到一个单一的连续时间基于分数的框架中，其中扩散由一个随机微分方程表示，可以逆转来生成样本。通过一个神经网络 sθ(xt,t) 逼近评分函数 ∇_(xt) ln⁡ p_t(xt) 来训练扩散模型。有关扩散模型的训练和采样的更多细节在附录 A 中描述。

4. 提出的方法：内在维度（Intrinsic Dimension）估计

考虑一个数据集

D ​∼ p0​(x)，它由 N 个独立的 d 维向量 x^(i) ∈ R^d 组成，这些向量从分布 p0(x) 中抽取。分布 p0(x) 的支持集在一个嵌入在 d 维环境空间中的 k 维流形 M 上。我们的目标是从 D 中推断出流形 M 的维度 k。

我们根据方差爆炸（VP） SDE dx_t = g(t)dw_t【Song 等，2020】来扰动数据，并训练一个神经网络 sθ(xt,t) 来逼近噪声扰动目标分布的评分函数，即 ∇_(xt) ln⁡ p_t(xt)，对于由扩散时间 t 索引的一系列扰动水平。我们使用带有似然加权的加权去噪分数匹配目标来训练模型，见【Song 等，2021】。有关扩散模型训练的更多细节可以在附录 B 中找到。

考虑一个流形 M 上的数据点 x_0​，并通过前向过程在短时间 t_0 内使用转移核（transition kernel）

将其扰动到环境空间中。如下一节所示，在 x_(t0)​​ 处，分数向量 sθ(x_(t0)​​, t0) 将指向其在 M 上的正交投影，使其几乎与 T_(x0)M 正交。由于这个原因，这个评分向量将几乎完全包含在 N_(x0)M（x_0 处的法向空间）中，因此在从 x_0 扩散的 K 个点上评估的评分向量组成的矩阵的秩不应超过 N_(x0)M 的维度。有了足够的样本，矩阵

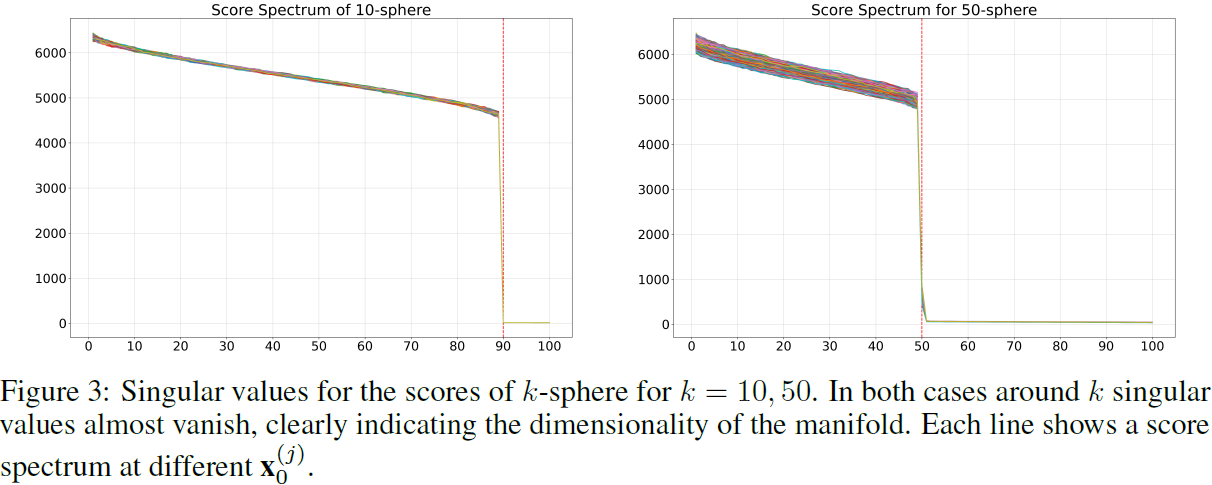
的秩估计了法向空间的维度，从中可以估计流形的维度。在我们的方法中，我们在时间 t0 = ϵ 采样 K = 4d 个扩散点，并计算 S 的 SVD，最终我们估计内在维度 ^k(x0) 为消失奇异值的数量。

结果谱图显示在法向空间的维度处或非常接近处有显著下降。剩下的非零但较小的奇异值对应于评分向量的切向分量。这个行为是预期的，因为评分向量不可避免地会有一个非常小的切向分量，原因将在后面的章节中解释。选择 ^k(x0) 的截断点通常在视觉上非常明显，但可以通过选择谱图中最大下降点来自动化：

在选择 x_0 时，我们理想上希望选择一个评分近似质量高、切向分量最小和流形曲率低的点。然而，由于这些因素是不可控的，我们随机选择多个 x^(j)_0 值并为每个值绘制一个谱图。对于简单的分布，评分谱图看起来相似，在准确值处有下降。对于更复杂的分布，下降位置随 x^(j)_0 的选择而变化。我们发现，最大估计的 ^k 提供了最好的估计结果。方法的理论理解支持这一点，详见后续章节。 

6. 局限性

在第 5 节中，我们确定了在给定足够小的 t 时的完美评分近似情况下，我们的方法能正确估计维度。然而，在实际操作中，我们的方法可能会遇到两类错误：近似误差和几何误差。近似误差是由于评分近似

不完美而产生的。几何误差（离散误差）则是在所选取的采样时间 t 不足够小时产生的，可能会影响我们方法的准确性，原因有二。首先，这可能导致评分向量的切向分量增加。其次，如果 x^(i)_t 离 M 太远，流形的曲率可能会导致不同 i 下的法向空间

产生差异。

我们通过实验证明了我们的方法对近似误差的稳健性，发现其对评分近似中的小误差具有稳健性。此外，我们分析了该方法对 p_0 非均匀性的敏感性，这可能在 t > 0 时引入轻微的切向评分分量。我们发现，使用最大

可以使我们的方法适应流形表面上不同程度的非均匀性，表现出比其他非线性估计器（MLE，局部PCA）更好的鲁棒性，而不需要减小 t。详见附录 G。

我们注意到定理 5.1 假设数据分布的支持完全在流形内。因此，我们通过实验研究了当数据集中在流形周围但不完全在流形内时方法的适用性。我们发现，对于 k-球体，只要数据紧密集中在流形周围，我们的方法仍然可靠。详见附录 G。

7. 实验

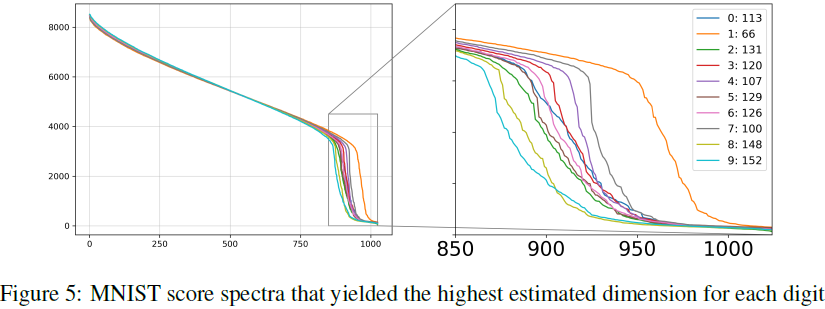
MNIST。在我们的研究中，我们还应用了所提出的技术来估计著名的 MNIST 数据集的内在维度——这是一个内在维度尚未确定的图像数据集。我们的研究结果表明，不同数字的内在维度存在差异。例如，数字 “1” 的估计维度为 66，而数字 “9” 的估计维度显著更高，为 152。这一差异可以归因于数字 “9” 固有的几何复杂性。图 5 通过显示每个数字的评分谱图阐明了这些观察结果，这些谱图产生了每个数字的最大估计维度。我们在表 1 中展示了每个数字的估计维度，附录 F.3 中包含了每个数字的完整谱图集。

8. 结论及进一步方向

在这项工作中，我们从理论上证明并通过实验验证了扩散模型可以从数据中推断出内在维度。我们引入了一种方法，通过预训练的扩散模型估计数据流形的内在维度。该方法利用了这样一个观察结果：在足够小的扩散时间下评估的扩散模型近似于数据流形的法向束（normal bundle）。我们的工作提供了双重贡献：它强调了扩散模型能够检测数据的低维结构，并提供了一种严格的内在维度估计方法。

我们的方法已经在欧几里得数据和图像数据上进行了严格测试，并且在内在维度的准确估计方面表现出一致性，尤其是在高维流形上优于已建立的统计估计器。此外，我们的研究引入了 MNIST 的维度的新估计，与在一系列潜在维度上训练的自动编码器的预测结果高度一致。

据我们所知，我们是第一个提出基于扩散模型的内在维度估计方法的人。我们的方法在高维流形上的优异表现归因于神经网络架构中近似评分函数的归纳偏差所带来的增强统计效率。我们的工作为理解和估计内在数据维度开辟了新途径，具有在机器学习领域的潜在影响。未来的研究应探索该方法在其他数据类型上的适用性及其在各个领域的潜力。