定理1(罗尔(Rolle)中值定理)
若函数f满足如下条件:
(i)f在闭区间[a,b]上连续;
(ii)f在开区间(a,b)上可导;
(iii)f(a)=f(b);
则在(a,b)上至少存在一点 使得
使得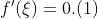
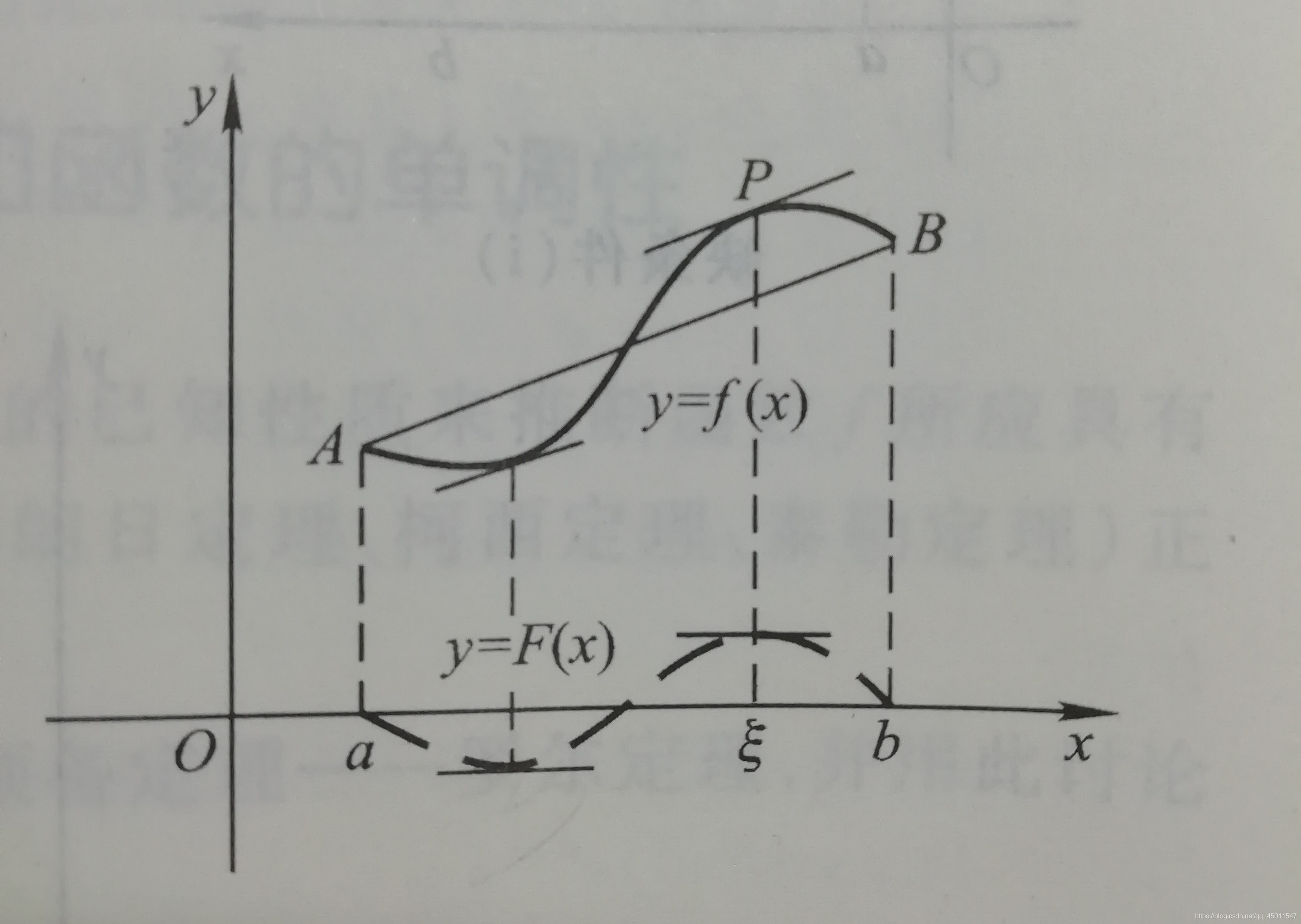
罗尔定理的几何意义:在每一点都可导的一段连续曲线上,如果曲线的两端高度相等,则至少存在一条水平直线,如图所示;
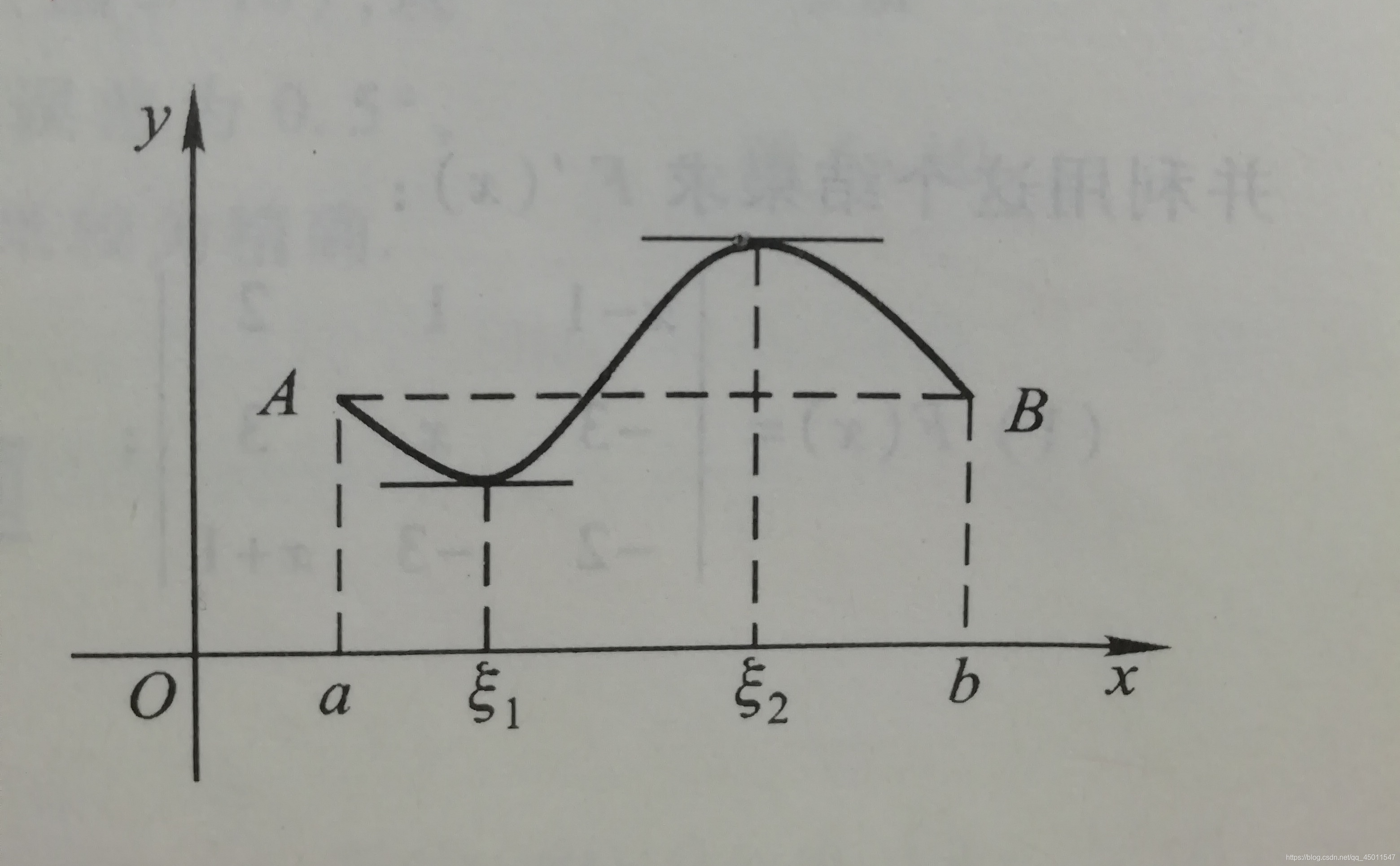
注:定理中的三个条件缺一不可。
定理2(拉格朗日(Lagrange)中值定理)
若函数f满足如下条件:
(i)f在闭区间[a,b]上连续;
(ii)f在开区间(a,b)上可导;
则在(a,b)上至少存在一点 使得
使得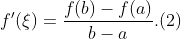
显然,特别当f(a)=f(b)时,本定理的结论即为罗尔定理的结论,这表明罗尔定理是拉格朗日定理的一个特殊情形。
拉格朗日中值定理的几何意义:在满足定理条件的曲线y=f(x)上至少存在一点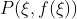 该曲线在该点处的切线平行于曲线两端点的连线AB,如图所示;
该曲线在该点处的切线平行于曲线两端点的连线AB,如图所示;
公式(2)称为拉格朗日公式.
拉格朗日公式还有几种等价表示形式:
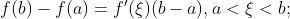
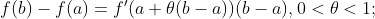
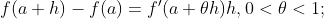
推论1:若函数f在区间I上可导,且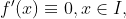 则f为I上的一个常量函数。
则f为I上的一个常量函数。
推论2:若函数f和g均在区间I上可导,且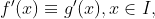 则在区间I上f(x)与g(x)只相差某一常数,即f(x)=g(x)+c (c为某一常数).
则在区间I上f(x)与g(x)只相差某一常数,即f(x)=g(x)+c (c为某一常数).
推论3(导数极限定理)
设函数f在点 的某邻域
的某邻域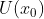 上连续,在
上连续,在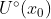 内可导,且极限
内可导,且极限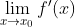 存在,则f在点
存在,则f在点 可导,且
可导,且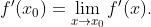
导数极限定理适合于用来求分段函数的导数。
定理3
设f(x)在区间I上可导,则f(x)在I上递增(减)的充要条件是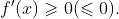
定理4
若函数f在(a,b)上可导,则f在(a,b)上严格递增(递减)的充要条件是:
(i)对一切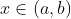 有
有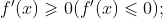
(ii)在(a,b)的任何子区间上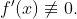
推论:设函数在区间I上可微,若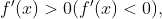 则f在I上严格递增(严格递减)。
则f在I上严格递增(严格递减)。
定理5(达布(Darboux)定理)
若函数f在[a,b]上可导,且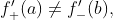 k为介于
k为介于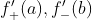 之间任一实数,则至少存在一点
之间任一实数,则至少存在一点 使得
使得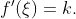
有时定理5称为导数的介值定理.
推论:设函数f(x)在区间I上满足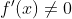 那么f(x)在区间I上严格单调。
那么f(x)在区间I上严格单调。
定理6(柯西中值定理)
设函数f和g满足
(i)在[a,b]上都连续;
(ii)在(a,b)上都可导;
(iii) 和
和 不同时为零;
不同时为零;
(iv)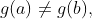
则存在 使得
使得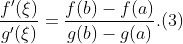
柯西定理的几何意义:把f,g这两个函数写作以x为参量的参数方程在uOv平面上表示一段曲线,如图所示,由于(3)式右边的
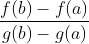 表示连接该曲线两端的弦AB的斜率,而(3)式左边的
表示连接该曲线两端的弦AB的斜率,而(3)式左边的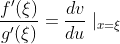 则表示该曲线上与
则表示该曲线上与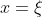 相对应的一点
相对应的一点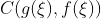 处的切线的斜率,因此(3)式即表示上述切线与弦AB互相平行。
处的切线的斜率,因此(3)式即表示上述切线与弦AB互相平行。
























 1327
1327

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








