cs231n 课程学习 三——反向传播算法

cs231n 课程学习 三——反向传播算法

cs231n 课程资源：Stanford University CS231n: Convolutional Neural Networks for Visual Recognition

我的 github 作业：FinCreWorld/cs231n: The assigments of cs231n (github.com)

一 简介

在本节将介绍反向传播算法（backropagation）。通过递归地使用链式法则，反向传播算法可以计算表达式的梯度。在下文中，我们给定一个输入向量 $x$，以及关于 $x$ 的函数 $f(x)$，随后计算 $f$ 关于 $x$ 的梯度（$\nabla f(x)$）。对于损失函数，样例 $(x_i,y_i)$ 以及权重 $W$ 和偏移矢量 $b$ 都是输入向量，但是我们重点关注损失函数 $L$ 关于 $W,b$ 的梯度，进而应用梯度下降算法。

二 简单表达式以及梯度的认识

首先从导数的定义开始
$$\frac{df(x)}{dx}=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$$
导数表示了函数在某一点的变化率，通过微分相关知识可以知道
$$f(x+h)=f(x)+h\frac{df(x)}{dx}$$
从而可以发现，在点 $x$ 处，如果 $x$ 增加了一个极小的量 $h$，那么函数值 $f(x+h)$ 就会相应的增加 $\frac{df(x)}{dx}$ 倍。即如果 $f^{\prime }(x)=3$，那么如果 $x$ 增加了 $h$，对应的 $f(x+h)$ 相比于 $f(x)$ 会增加 $3h$。

我们将情况扩展到二元函数
$$f(x,y)=xy$$
对该函数求偏导，有
$$\frac{\partial f}{\partial x}=y\frac{\partial f}{\partial y}=x$$
同理的，如果 $x,y=3,4$，那么 $f(x,y)$ 在 $x$ 增加 $h$ 时，其函数值增加 $4h$

由于其有两个自变量，因此我们使用梯度的概念代替导数的概念，梯度是一个向量
KaTeX parse error: Undefined control sequence: \pmatrix at position 11: \nabla f=\̲p̲m̲a̲t̲r̲i̲x̲{\frac{\partial…
对于函数 $f(x,y)=\max (x,y)$，有
$$\begin{gathered} \frac{\partial f}{\partial x}=1x\ge y \\ \frac{\partial f}{\partial y}=1y\ge x \end{gathered}$$

三 复合表达式以及链式法则的应用

我们给出一个稍微复杂的表达式，并应用链式法则求解问题，给定下列函数
$$f(x,y,z)=(x+y)z$$
我们可以将其看做如下形式
$$f(x,y,z)=qzq=x+y$$
则有
$$\begin{array}{r}\frac{\partial f}{\partial q}=z\frac{\partial f}{\partial z}=q\\ \frac{\partial q}{\partial x}=1\frac{\partial q}{\partial y}=1\end{array}$$
如果我们应用链式法则，就可以得到
KaTeX parse error: Expected 'EOF', got '&' at position 2: &̲\frac{\partial …
我们可以绘制如下计算过程图

绿色数字表示正常计算的值，已知 $x=-2,y=5,z=-4$ 进一步计算出 $q$ 的值，最后算出 $f=-12$。而红色的值表示反向传播的梯度，首先 $f$ 针对本身的梯度为 $1$，随后计算出 $dz=3$，$dq=-4$，最后算出 $dx=dy=dq=-4$（$\frac{\partial q}{\partial x}=\frac{\partial q}{\partial y}=1$）

进一步的，可以这样理解反向传播算法。每一次运算看做一个门，在正向运算中，计算出运算值以及针对输入的偏导数，在上例中，数据经过 + 时，计算出 $q$ 值以及 $\frac{\partial q}{\partial x}=\frac{\partial q}{\partial y}=1$，数据经过 * 时，计算出 $f$ 值以及偏导 $\frac{\partial f}{\partial q}=z\frac{\partial f}{\partial z}=q$。随后进行反向传播计算，初始时 $f$ 的输出偏导为 1，沿着计算路径反向传播，每经过一个门，就将 $f$ 相对于该门输出的偏导乘上该门输出相对于该门输入的偏导，从而得到$f$ 相对于该门输入的偏导。

四 使用模块化思想简化反向传播算法

给定一个函数
$$f(w,x)=\frac{1}{1+e^{-(w_0{x}_0+w_1{x}_1+w_2)}}$$
我们可以将其拆解称若干单步运算，将运算图绘制如下

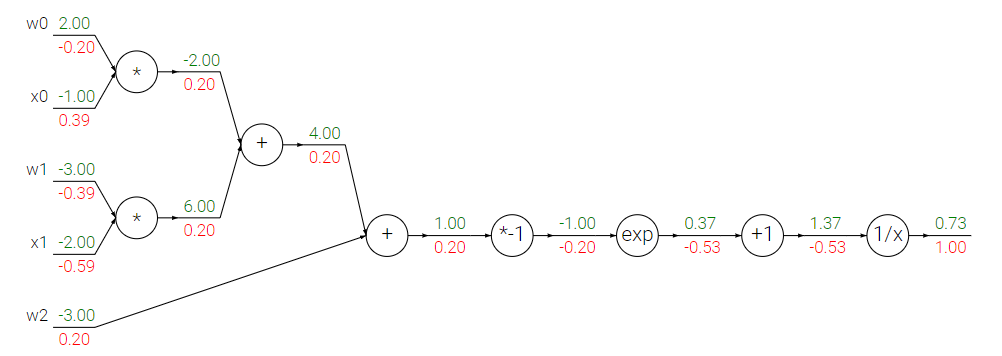
我们可以发现上述表达式的链过长，我们可以将几个相连的运算打包成一个运算。我们可以发现上述函数由点积和sigmoid函数复合而成。我们在运算时无需将sigmoid函数拆解，而是将其看做一个独立的运算即可。
$$\begin{gathered} \sigma (x)=\frac{1}{1+e^{-x}} \\ \frac{d\sigma (x)}{dx}=\frac{e^{-x}}{(1+e^{-x}{)}^2}=(1-\sigma (x))\sigma (x) \end{gathered}$$
因此我们可以简化上图中的最后一部分计算，针对 sigmoid 函数我们无需拆解运算步骤使用反向传播算法，直接代入公式即可。

数据预处理的重要性：对于乘法运算，比如 $f=w\ast x$，则 $\frac{df}{dw}=x$，如果我们的输入样例拥有较大的数值，比如 1000，那么 $w$ 的梯度就会很大，因此我们需要进行数据预处理，将所有数据减去均值，甚至除以方差，进行规范化处理。

五 向量运算

我们拥有权重矩阵 $W_{D\times M}$ 以及训练数据 $X_{N\times D}$，在线性分类器中，我们通常会进行如下计算
$$Y=XW$$
其中 $Y$ 表示对于所有样例我们在不同类别上的分数。随后我们会使用 $Y$ 计算损失函数，得到损失函数值 $L$，$L$ 为标量。假设我们根据损失函数（softmax或者svm损失函数）已经计算得到了 $\frac{\partial L}{\partial Y}$，则有
KaTeX parse error: Undefined control sequence: \pmatrix at position 33: …}}{\partial Y}=\̲p̲m̲a̲t̲r̲i̲x̲{ \frac{\partia…
即 $L$ 对 $Y$ 的偏导为一个与 $Y$ 相同形状的矩阵，表示 $L$ 对于 $Y$ 中每一个元素的偏导。

我们需要计算 $\frac{\partial L}{\partial X}$ 以及 $\frac{\partial L}{\partial W}$ 的值，通过链式法则，我们可以得到
$$\frac{\partial L}{\partial X}=\frac{\partial L}{\partial Y}\frac{\partial Y}{\partial X}\frac{\partial L}{\partial W}=\frac{\partial L}{\partial Y}\frac{\partial Y}{\partial W}$$
但是我们很少将 $\frac{\partial Y}{\partial X}$ 显示的计算出来，因为该矩阵拥有 $M\times N\times N\times D$ 个元素，计算量较大。我们可以充分利用线性分类器的特性，化简偏导

考虑 $L$ 对于 $x_{i,j}$ 的偏导数，有
$$\begin{array}{rl}\frac{\partial L}{\partial x_{i,j}}& =\sum _{s=1}^N\sum _{t=1}^M\frac{\partial L}{\partial y_{s,t}}\frac{\partial y_{s,t}}{\partial x_{i,j}}\\ & =\frac{\partial L}{\partial Y}\cdot \frac{\partial Y}{\partial x_{i,j}}\end{array}$$
其中 $\cdot$ 表示内积。

其中
KaTeX parse error: Undefined control sequence: \pmatrix at position 40: …tial{x_{i,j}}}=\̲p̲m̲a̲t̲r̲i̲x̲{ 0 & 0 & 0 & \…
其中仅第 $i$ 行有值，其余行皆为 0，因此
$$\begin{array}{rl}\frac{\partial L}{\partial x_{i,j}}& =\frac{\partial L}{\partial Y}\cdot \frac{\partial Y}{\partial x_{i,j}}\\ & =\frac{\partial L}{\partial y_{i,1}}\ast w_{j,1}+\frac{\partial L}{\partial y_{i,2}}\ast w_{j,2}+\cdots +\frac{\partial L}{\partial y_{i,M}}\ast w_{j,M}\\ & ={\frac{\partial L}{\partial Y}}_i{W}_j^T\end{array}$$
则
KaTeX parse error: Undefined control sequence: \pmatrix at position 49: …}{\partial X}&=\̲p̲m̲a̲t̲r̲i̲x̲{ \frac{\partia…
至此我们推导出来了公式！

综上，对于 $N\times D$ 矩阵 $X$，$D\times M$ 矩阵 $W$，以及公式 $Y=XW$，以及关于 $Y$ 的损失函数 $L$，假设我们已知 $\frac{\partial L}{\partial Y}$，计算 $\frac{\partial L}{\partial X}$ 时我们无需显示的计算 $\frac{\partial Y}{\partial X}$，而是通过公式
$$\begin{array}{rl}\frac{\partial L}{\partial X}& =\frac{\partial L}{\partial Y}{W}^T\end{array}$$
即可计算结果。同样的，我们可以推出
$$\begin{array}{rl}\frac{\partial L}{\partial W}& =X^T\frac{\partial L}{\partial Y}\end{array}$$
一个便捷的方法是通过矩阵相乘维度的变化来确定公式。$\frac{\partial L}{\partial W}$ 是 $D\times M$ 维，唯一能够得出该维度的是 $X^T$ 与 $\frac{\partial L}{\partial Y}$ 相乘。综上，我们推出了关于线性层的偏导法则。结合损失函数（softmax、svm）的偏导，再利用反向传播算法，我们就能够轻易的计算出损失函数关于任意输入的偏导。