GAMES101: 现代计算机图形学入门（2）几何、光线追踪

浮沉丶奕辻琮

已于 2024-08-05 14:32:01 修改

阅读量605

点赞数 1

分类专栏： GAMES101 文章标签：算法图形渲染

于 2023-05-24 19:59:54 首次发布

本文链接：https://blog.csdn.net/qq_45617648/article/details/130135936

版权

GAMES101 专栏收录该内容

2 篇文章 1 订阅

订阅专栏

GAMES101: 现代计算机图形学入门
链接：GAMES101

1. 几何

1.1 几何的表示

隐式几何：通过一个函数表达式来表示的几何体，即 f(x，y，z)=0。

优点：很容易判断一个点在不在几何体上。
缺点：很难通过表达式看出几何体的形状。

显式几何：通过参数映射的方法来表示的几何体，即每个（u，v）都有对应的（x，y，z）。

优点：我们只需遍历所有的（u，v）即可得到几何的形状。
缺点：很难判断一点是否在几何体上。

1.2 隐式几何

1.2.1 CSG（Constructive Solid Geometry）

基本的几何体通过基本的运算（交、叉、并）得到的复杂几何体，这操作被称为CSG。

1.2.2 距离函数（SDF）

距离函数：任何一个点到达边界的最短距离，在内部为正，在外部为负。

我们想要得到一个逐渐混合的东西，比如下面的融合就需要用上图的SDF的混合，而不是原本的混合。通过距离函数的融合，相当于实现了表面特征的融合。

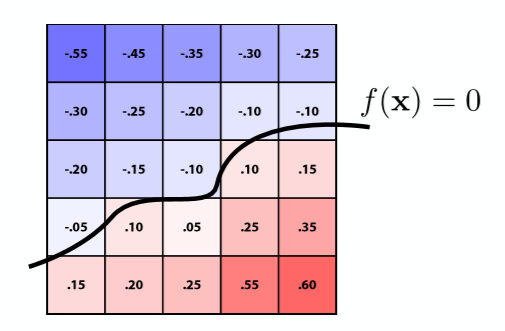
几何体的边界，即为SDF=0，类似于等高线，下图为水平集的表示方法，当然有其他方法。

1.2.3 分型

特点：自相似，自己和整体长得很像，与递归结构一致。

1.3 显式几何

1.3.1 点云

点云是空间中很多很多点的集合，只要点足够密集那么一定能表示任意的几何体。
如果点云的点不够密集，那么就会看不出形状。

1.3.2 多边形网格

将面拆分为三角形或者四边形，存储三角形的顶点信息。

使用.obj的文件存储几何体的顶点（v）、面的法线（vn）、纹理坐标（vt）和这三者之间的关系（f）。关系的表示方式f(v/vt/vn)，即三角形由哪三个顶点，哪三个纹理坐标，哪三个法线来表示。

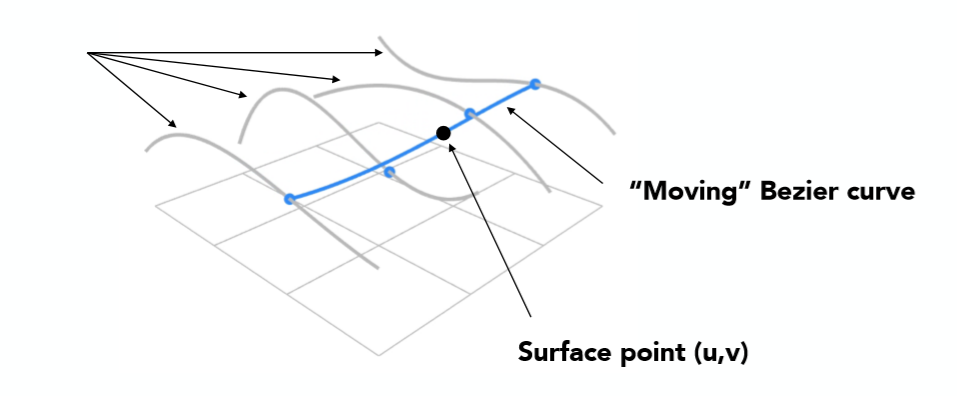
1.3.3 贝塞尔曲线

一定要经过起止点，若干个控制点用于控制曲线弯曲的方向，最终形成一条光滑的曲线。

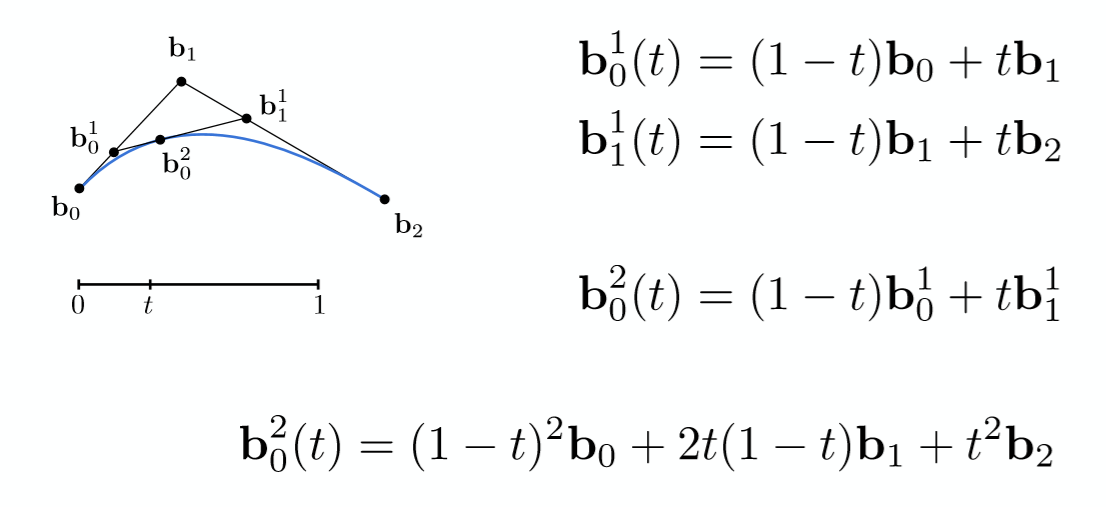
用t在各点之间不断的做lerp插值，最终会递归成一条光滑的曲线。

分析即可得到代数表达式为一个二项分布的多项式，称为伯恩斯坦多项式。

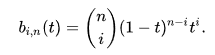
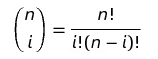
贝塞尔曲线的性质：
（1）在仿射变换下，贝塞尔曲线不变，也就是可以直接对曲线进行仿射变换；而在投影变换下，贝塞尔曲线会变。
（2）凸包性质：连接最外围的控制点，贝塞尔曲线一定在连出来的凸包内。特殊的，控制点为一条直线，贝塞尔曲线即为相同的直线。
（3）逐段的贝塞尔曲线：如果点太多，我们一般每4个控制点定义一条光滑的贝塞尔曲线。
（4）CN连续性：为了保证逐段的贝塞尔曲线的光滑连接，我们需要保证连续。C0连续：一段的终止点等于下一段的起点；C1连续：终止点等于起点，并且该点为两边的中点。

其它的曲线
B-Splines（Basis Splines）：奇函数样条线，拥有局部性（拖拽一两个点，不影响整体）。
本节课不深入介绍，详情了解：清华大学-计算机图形学基础（国家级精品课）

1.3.4 贝塞尔曲面

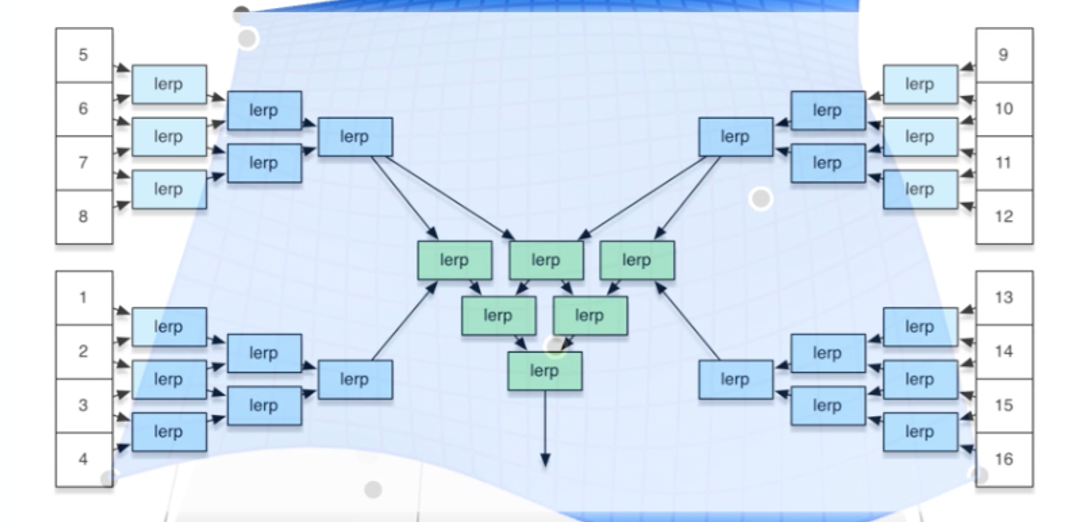
用16个点去控制形成的曲面，先在u方向的形成4条贝塞尔曲线，再在4条贝塞尔曲线上，在v方向控制出最终的点（u，v）。

1.4 网格细分

1.4.1 Loop细分

注意：Loop不是循环，而是发明者的名字。
loop细分直接用三角形三条边的中点拆分为4个三角形，先细分再调整。
对于新的顶点，我们对其周围的原来的点求平均。

对于原来的顶点，我们认为不止和邻近的原来顶点的值有关，还与自己的值有关，因此求个加权。即邻近的顶点很多，那么更多的相信邻近的点，如果邻近的顶点很少，更多的相信自己。
定义：n为顶点的度（连接边的数量），u为与度有关的数，如果n=3，u=3/16，其余情况下u=3/(8n)。

1.4.2 Catmull-Clak细分

我们定义
（1）四边形面：四条边的面
（2）奇异点：度不为4的点
我们注意到，在非四边形面上点一个中点，因为该点要与各边中点相连，那么该点一定是奇异点，同时该非四边形面会减少。

同时，定义顶点的变化，都是平均的方式进行细分。
定义：f为面上的中点（新点），e为边上的中点（新点），v为原来的点（老点），p为该点自己（老点）。

2. 光线追踪

2.1 阴影图（Shadow Mapping）

2.1.1 硬阴影

从光源看向场景，记录所有能看到点的深度，形成一张深度图。
从真正的摄像机看向场景，把所有能看到的点投影回光源的位置，形成另一张深度图。
比较两张深度图，深度相同的，即为能看到的，深度不同的就是阴影。

2.1.2 软阴影

软阴影是针对光源有一定大小的优化，如下图的半阴影区。

2.2 Whitted-Style 光线追踪

Whitted-Style即模拟光线不断弹射的过程（光线的反射和折射）。

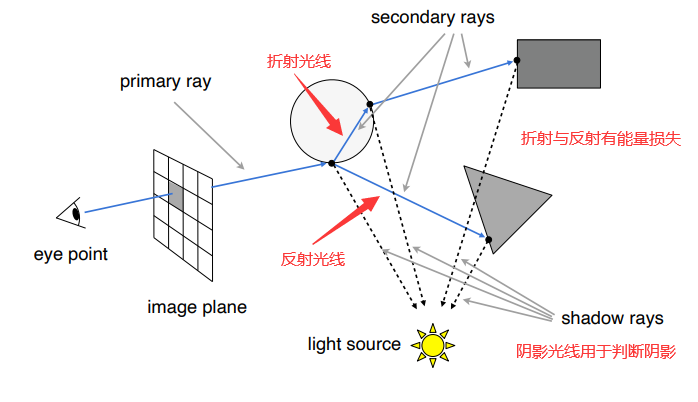
2.2.1 光线的定义

注意：规定光线沿直线传播，不考虑其波动性，光线与光线之间不会碰撞，所有的光线可理解为光源射向我们的眼睛。

我们将光线理解为从一个点出发，向某一方向发出的射线。

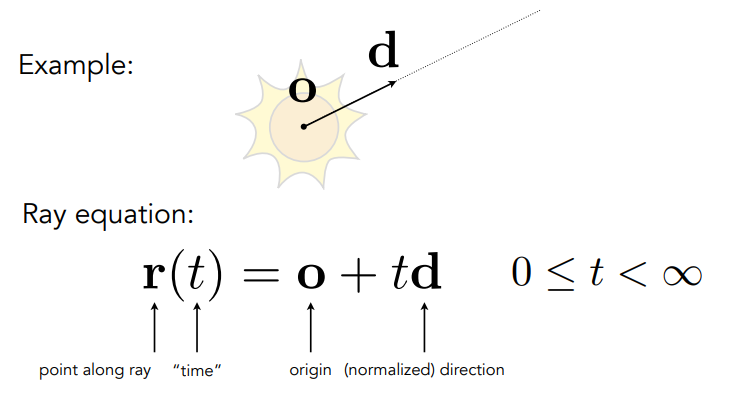
注意：光线定义中的r(t)一定是一个点。

2.2.2 光线与球面求交

球面的方程：球上的点到球心的距离等于半径。

2.2.3 光线与三角形面求交

我们拆分为两部分，第一步我们求光线与三角形所在的平面求交，第二步判断该点是否在三角形内。
平面的方程：利用点法式写出平面的方程。

我们将光线的方程与平面的方程联立求解，求出t。

使用MT算法进行优化（三角形内部点的方程使用重心坐标写出，再进行联立求解）。

符合正解的条件：t，b1，b2均为正数。

2.3 加速结构

我们把光线与所有的三角形都要求交，弹射多次计算过程会非常慢，因此我们需要加速这一过程。

2.3.1 包围盒

包围盒（Bounding Volumes）：我们使用简单的形状将物体包起来。
如果光线连包围盒都碰不到，那更不可能碰到包围盒中的物体，以下为二维的包围盒。

对于三维空间的长方体，我们理解为三对不同的沿x、y、z轴的对立面组成的集合，即轴对齐包围盒（AABB）。

2.3.2 光线与包围盒求交

我们以二维为例，我们对所有轴都做与之相交的tmin和tmax，最后我们算出最大的tmin和最小的tmax。

对于三维也是一样，当光线进入三个对立面时，才算进入盒子，当光线出了一个对立面，就算离开盒子了。

检查进入的时间小于离开的时间那么光线一定会进入盒子一段时间。
检查离开的时间是否小于0，即盒子一定早于射线，不可能穿过盒子，一定没有交点。
检查离开的时间大于等于0，但是进入的时间小于0，即光线一定在盒子里，光线与盒子一定有交点。

综上我们得出光线与盒子有交点的条件为：进入时间小于离开时间，并且离开时间要大于0。
对于包围盒求交点的优化：我们联立算出对立面的其中一个，又因为平行，就可以算出另一个对立面的参数t。

（1）在光线追踪之前，首先找到包围盒，把包围盒分成一个个格子的网格。
（2）遍历网格，若网格中存在物体的表面使用灰色标记。

（3）以光线射的方向开始计算，计算出光线能遍历到的网格，如下图光线方向，只需判断右和上面的格子。（光栅化一条线）
（4）判断网格中是否存在物体表面（即灰色标记），若有则光线有可能和物体相交，进一步判断光线与物体求交。

注意：如何定划分的网格数量？格子的数量 = C * 物体的数量，C = 27，当然实际情况中不一定。

2.3.3 空间划分

实际情况下，物体在场景中一定是不均匀的，因此我们的网格划分也应该不均匀，引出了很多空间划分的分类。

Oct-Tree：八叉树，在三维空间中，每次均匀的分为8块。
KD-Tree：每次以轴向方向划分为两部分，一般以不同轴向交替划分，因此每次细分为两部分，结构类似二叉树。
BSP-Tree：与KD-Tree类似，只是不是以轴向方向进行划分，因此很难计算。

由于KD-Tree好算且优良，我们以KD-Tree为例分析。
KD-Tree划分步骤：

我们以KD-Tree划分的方式构建二叉树，使用AABB，从根节点开始判断所有点与光线是否存在交点。若存在交点，则该点的两个子节点都可能存在交点，逐层往下判断直至判断到叶子结点。
注意：中间的结点只存储指针，叶子结点才存储实际的物体。

KD-Tree的缺点：
（1）难以判断划分的包围盒与物体构成的三角形是否相交，即盒子如何与三角形求交的问题。
（2）同一个物体可能划分到了两个不同的包围盒中。

2.3.4 物体划分

BVH（Bounding Volume Hierarchy）是对物体进行划分，为解决KD-Tree的缺点，我们可以选择使用BVH。
划分步骤：
（1）按照三角形进行划分，一个物体只可能存在在一个包围盒中。
（2）找到一个包围盒，使用递归直接对包围盒中的三角形进行分组，分成两部分，再重新计算他们的包围盒。
（3）当叶子节点中存在足够少的三角形就停止划分。

注意：
（1）每次划分沿着最长的轴进行划分，同时划分沿着xyz轴。
（2）划分时通常寻找一个变量的中位数进行划分，保证划分出的树接近平衡，便于查找。对于这个变量我们可以选择三角形的重心坐标，此处可以用排序的更多算法（TopK问题、快速选择）自行了解。

Intersect(Ray ray, BVH node) 
{  
    /** 光线与盒子不相交 */
    if (ray misses node.bbox) 
        return;
    /** 光线与盒子相交，且节点是叶子节点 */
    if (node is a leaf node)     
        test intersection with all objs; // 判断盒子中所有的三角形
        return closest intersection; // 返回最近的一个三角形
    /** 光线与盒子相交，且节点不是叶子节点 */
    hit1 = Intersect(ray, node.child1); // 递归判断
    hit2 = Intersect(ray, node.child2);
    return the closer of hit1, hit2; 
}

2.4 路径追踪

由于Whitted-Style 光线追踪的效果不真实，我们要研究真实的物理量，因此引入辐射度量学，也就是路径追踪。
我们定义光照的几个属性：
（1）Radiant Energy
（2）Radiant Flux
（3）Rediant Intensity
（4）Rediant Irradiance
（5）Radiant Radiance

2.4.1 辐射度量学

1. Radiant Energy（Q）
定义：光线辐射出来的能量，用Q表示，单位为J（焦耳）。

2. Radiant Flux
定义1：单位时间内的能量，与功率类似，单位为W（瓦特）或者 lm（流明）。
定义2：在物理上，理解为单位时间内通过一个感光平面的光子的数量。

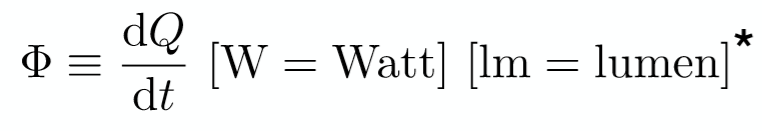
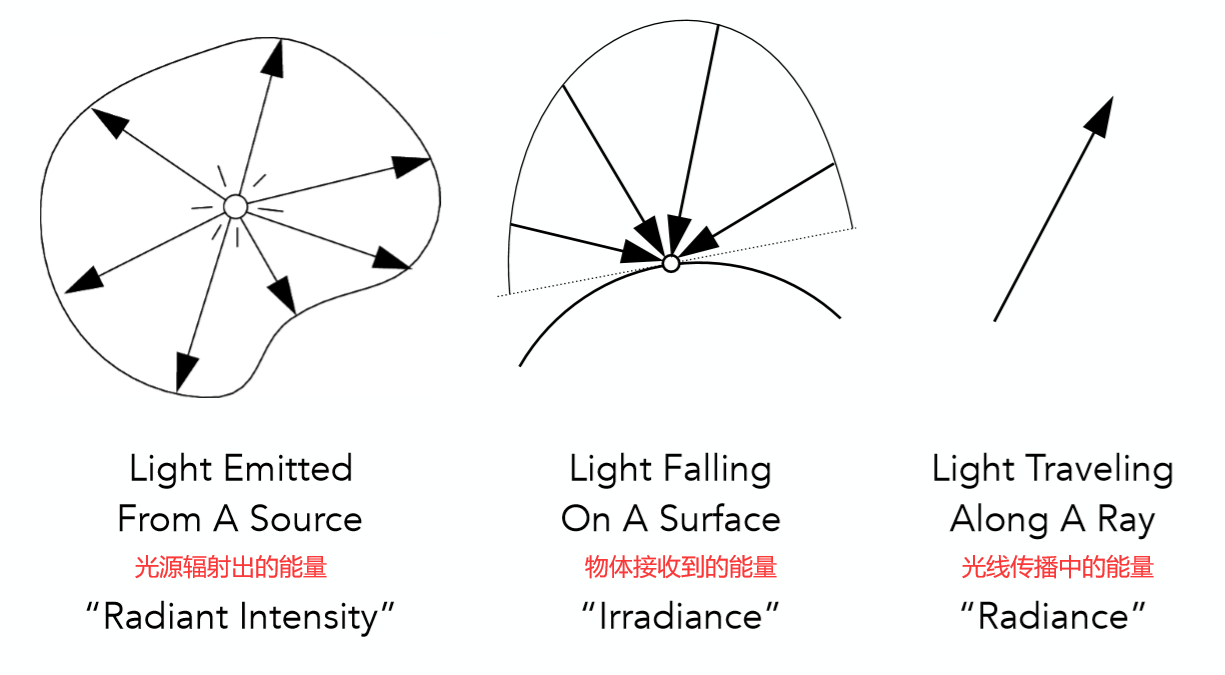
3. Rediant Intensity（I）
定义：单位立体角上功率的大小，用I表示，单位为cd（坎德拉）。

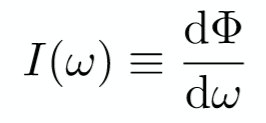
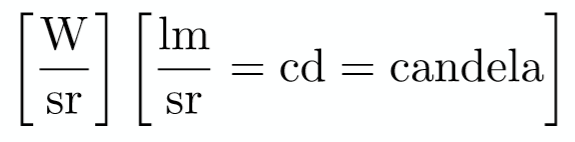
弧度制：θ=l/r，l为弧长，r为半径。整个圆弧度为2π。
立体角：以w方向投影到球面坐标系中，并以dθ和dϕ表示。（极小的变化求微分）

dw为立体角微分，A为圆面积，r为半径。整个立体角为4π。

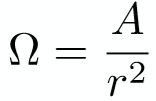
对于点光源，立体角为4π。

4. Rediant Irradiance（E）
定义：单位面积上，某个点接收到的功率，用E表示，单位为Lux（勒克斯）。

此功率方向与面积法线方向一致，需要处理成投影的cosθ

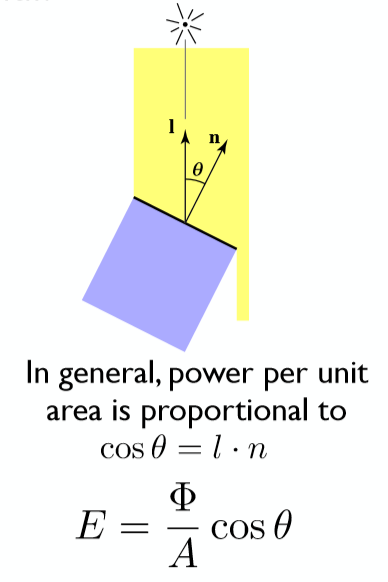
5. Radiant Radiance（L）
定义：单位面积上，单位立体角上，某个点接收到的功率，用L表示，单位为nit（尼特）。

注意：我们考虑dA入射和出射的能量。

Rediant Irradiance与Rediant Radiance的区别：
Irradiance是一个点接收到来自所有立体角的光线的能量。
Radiance是一个点接收到来自某一立体角的光线的能量。
因此Irradiance可看做所有立体角的Radiance求和。

2.4.2 双向反射分布函数（BRDF）

BRDF（Bidirectional Reflectance Distribution Function）
我们将反射理解为光线打到一个点上，光的能量被点吸收了，剩下的能量就是反射出去的能量。这与材质相关，因此BRDF可以定义材质的反射光的能力。
BRDF定义了一个点沿某个立体角反射出的L与沿某个方向接收到的E之间的比值，因此表示了入射光与反射光的比例关系。

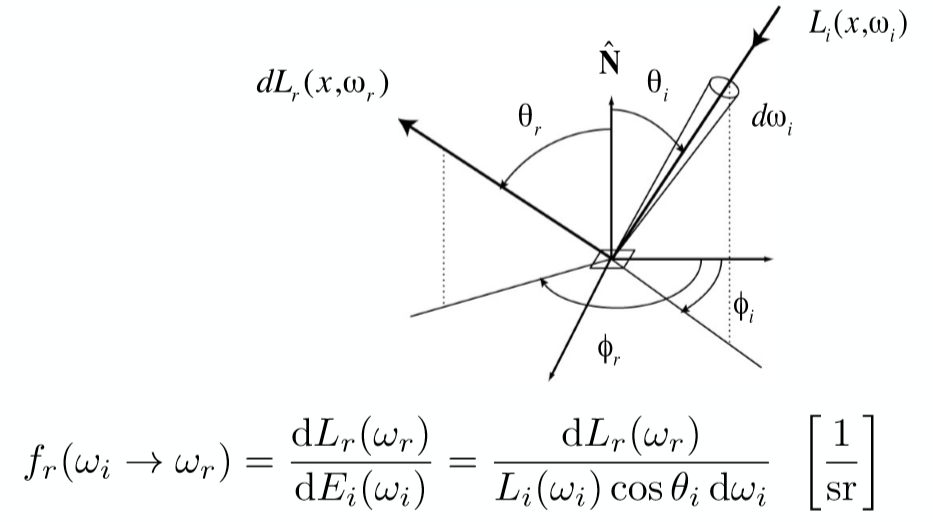
我们将所有的入射立体角进行积分，我们能得到沿某一方向出射的L。
这就是反射方程，研究了在不同方向光照的情况下，我们规定一个特定的观测方向，观察到的L.。

2.4.3 渲染方程

渲染方程定义了自发光Le和反射光，即渲染方程等于自发光加上反射方程。

注意：n·wi = cosθ
渲染方程定义了所有光线传播的规律，渲染方程也是现代图形学的基础！

我们将渲染方程写成数学表达，采用微分算子和二项式定理进行求解。

注意：
（1）E为自身的能量，KE为一次反射的能量（直接光照），K2E为两次反射的能量（间接光照），以此类推。
（2）L可简单的理解为全局光照，即直接光照+间接光照。
（3）光栅化只能做E+KE（光源自己和直接光照），后面的光栅化很难实现，而光线追踪就是解决后面部分的。
（4）K一定小于1，所以全局光照一定会收敛到一个值，而不会一直变亮。

上面的效果是直接光照（左图），加上反射一次后的全局光照（右图），光栅化一般只得到左图的结果。

2.4.4 蒙特卡洛积分

蒙特卡洛积分是去用概率论的办法来求一个定积分的值，我们对函数域进行多次采样，采样值求出一个均值作为均值的近似值。

使用蒙特卡洛积分去求解渲染方程

使用蒙特卡洛积分，相当于朝所有方向随机的打一条射线，如果打中就求解对应的渲染方程，打中的概率即为pdf(wi)，pdf(wi)因为是对半球上立体角的平均，所以是1/2π。

/** 直接光照的路径追踪 */
shade(p, wo)
    Randomly choose N directions wi~pdf
    Lo = 0.0
    For each wi
        Trace a ray r(p, wi)
        If ray r hit the light
            Lo += (1 / N) * L_i * f_r * cosine / pdf(wi) // 应用蒙特卡洛积分
    Return Lo

通过递归的方法直接能写出全局光照的路径追踪。

/** 全局光照的路径追踪 */
shade(p, wo)
    Randomly choose N directions wi~pdf
    Lo = 0.0
    For each wi
        Trace a ray r(p, wi)
        If ray r hit the light
            Lo += (1 / N) * L_i * f_r * cosine / pdf(wi)
        Else If ray r hit an object at q
            Lo += (1 / N) * shade(q, -wi) * f_r * cosine / pdf(wi) // 应用蒙特卡洛积分递归地求间接光照
    Return Lo

上述代码会出现的问题与解决：
（1）如果使用递归的方法，第一次假设是100个，第二次就会递归成10000个，增量是指数级的。只有当蒙特卡洛积分的采样为1时才不会出现指数级的爆炸，因此我们用N = 1来解决，这就是路径追踪（N = 1），而分布式光线追踪（N != 1）此处不管。

shade(p, wo)
    Randomly choose ONE direction wi~pdf(w) // 只选择一个w
    Trace a ray r(p, wi)
    If ray r hit the light
        Return L_i * f_r * cosine / pdf(wi)
    Else If ray r hit an object at q
        Return shade(q, -wi) * f_r * cosine / pdf(wi)

而N = 1一定会造成很大的误差，因此我们选取多个路径求平均。

ray_generation(camPos, pixel)
    Uniformly choose N sample positions within the pixel
    pixel_radiance = 0.0
    For each sample in the pixel
        Shoot a ray r(camPos, cam_to_sample)
        If ray r hit the scene at p
            pixel_radiance += 1 / N * shade(p, sample_to_cam) // 选取N个不同的位置，每次shade求平均
    Return pixel_radiance

（2）递归没有结束条件，因此会无限循环。我们可以使用Russian Roulette（俄罗斯轮盘赌）的方法，选取随机数，让其会停止递归，如果随机值不用停止，我们返回L/P，如果停止，我们返回0，最终的期望一定和原值L一致。

核心思想：使用Russian Roulette（俄罗斯轮盘赌），即无偏估计；利用期望E不变并限制P来随机解决问题。

shade(p, wo)
    Manually specify a probability P_RR
    Randomly select ksi in a uniform dist. in [0, 1] // 产生一个随机数
    If (ksi > P_RR) return 0.0; // 如果限制条件，则直接返回0

    Randomly choose ONE direction wi~pdf(w)
    Trace a ray r(p, wi)
    If ray r hit the light
        Return L_i * f_r * cosine / pdf(wi) / P_RR
    Else If ray r hit an object at q
        Return shade(q, -wi) * f_r * cosine / pdf(wi) / P_RR

2.4.5 提高效率

我们如果只用均匀的方法进行蒙特卡洛积分，那么对于光源很小的情况，可能就需要很多光线才能成功。

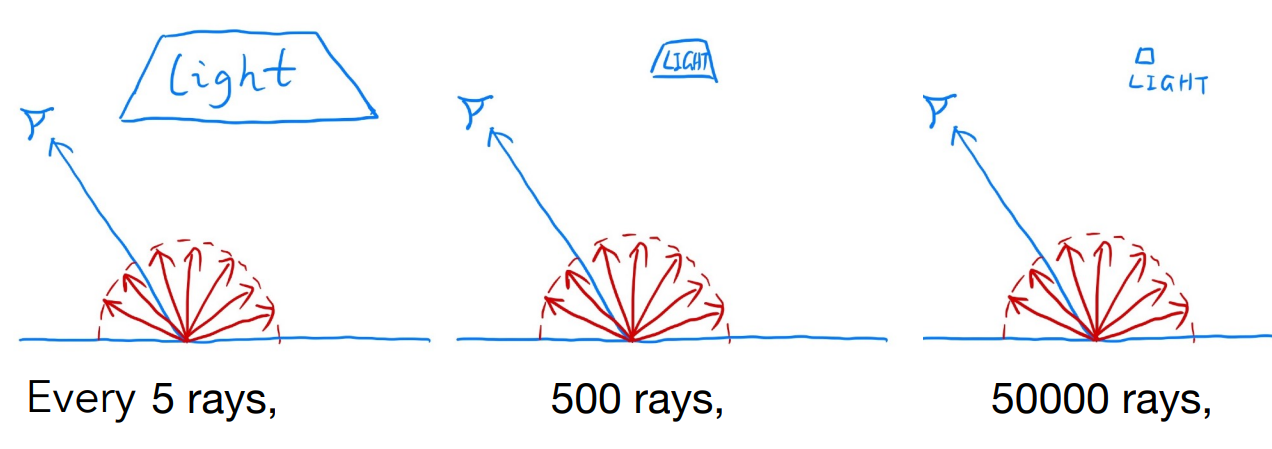
因此我们为了改进，我们只对光源进行采样，把渲染方程写成对光源表面积的积分。

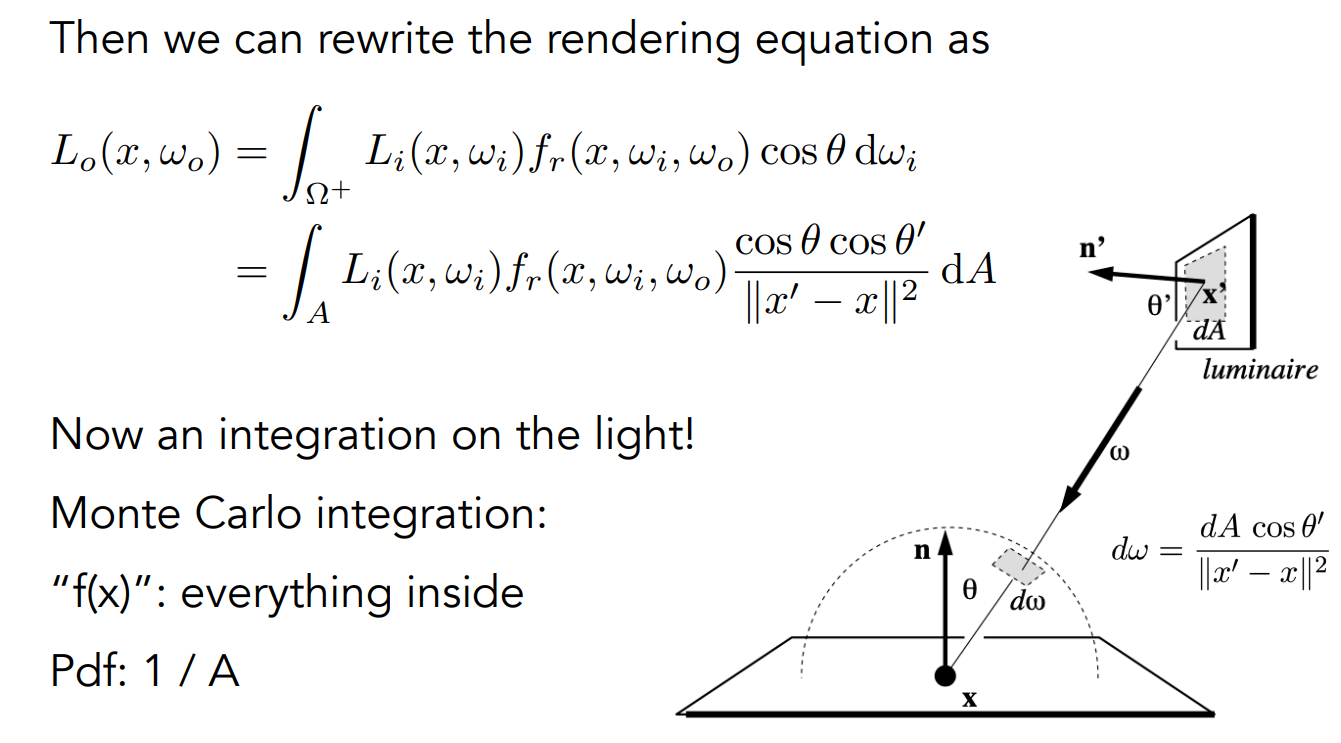
shade(p, wo)
    // 直接从光源射出的射线，转换到dA面积上积分
    Uniformly sample the light at x’ (pdf_light = 1 / A)
    L_dir = L_i * f_r * cos θ * cos θ’ / |x’ - p|^2 / pdf_light
    // 其他的反射光线
    L_indir = 0.0
    Test Russian Roulette with probability P_RR
    Uniformly sample the hemisphere toward wi (pdf_hemi = 1 / 2pi)
    Trace a ray r(p, wi)
    If ray r hit a non-emitting object at q
        L_indir = shade(q, -wi) * f_r * cos θ / pdf_hemi / P_RR
    Return L_dir + L_indir

2.5 光线追踪遗留问题

课程中未讲到的问题，之后可自行了解：
（1）怎么对函数进行采样，给你任意一个函数怎么采样它（采样理论）
（2）选择什么样的pdf（重要性采样理论）
（3）选择什么样的随机数（low discrepancy sequences）
（4）采样方法的混合，比如上面的对面积采样和对半球采样的混合（multiple imp. sampling）
（5）为什么所有的Radiance的平均就是单个像素的Radiance（pixel reconstruction filter）
（6）对一个像素来说，Radiance怎么转化为Color（伽马矫正，曲线，颜色空间）