自动控制原理＜二＞

二、稳定性分析（stability）

在建立一个控制系统的过程中，系统的稳定性是系统的基础，常说判定系统优劣的三要素有稳、准、快。第一要素就是稳，只有在稳定的系统中才有准确性和快速响应的说法。并才能达到的控制的目的以及可以进一步进行优化控制器,可以用下图金字塔进行简单的表现稳定性的重要性：

图1：稳定性金字塔

那么怎么去判断一个系统的稳定性呢？在控制系统中我们常常把一个系统先转换到用复频域来表示（因为在复频域中可以将积分微分简化为简单的s和1/s），简化了分析。那么在复频域要怎么去判断稳定性？这有是一个问题。书上说只要保证复频域系统传递函数的极点只要分布在虚轴的左半平面系统就平衡，让我们一步步来看这是为什么？

图2：极点分布在虚轴的左半平面

我们先来看一个简单的例子，分别描述了三种系统：

• 不稳定系统A
• 临界稳定系统B
• 稳定系统C

依次从左到右表示：不稳定系统A、临界稳定系B、统稳定系统C。

在理想的环境下，当施加一个外力时

系统A：小球将无止境的一直加速下滑，系统将再也回不到原始的稳定点。

系统B：小球将在一个稳定的轨迹范围内做往返运动，系统不可能回到原始的稳定点。

系统C：小球在摩擦力的作用下，经过一段时间小球将回到稳定的位置。

• 让我们进一步从闭环系统分析一下系统C为什么可以达到稳定

首先我们先要知道稳定的标准，在此系统中稳定就是小球停止。那么我们可以得到如下关系

输入量：外力

输出量：加速度

反馈量：摩擦力

​ 我们说在闭环系统中，输出量的大小往往决定了输入量的多少，所以通过建立输出量，输入量，反馈量的方程

很简单的就可以得到此系统是一个闭环的负反馈系统，从而使系统能够达到稳定的效果。

我们刚刚通过一个简单的例子，我们大概的知道了稳定的主观表现形式，其实就是使一个系统趋向于一个固定的设定值。那么系统稳定性在客观的传递方程中是一个什么样的提现呢？我们先来讨论一下什么是极点什么是零点。如下图所示：

图3：传递函数中的零极点

D(s)：分子为零是零点,，常用Zi表示

N(s)：分母为零是极点，常用Pi表示

现在我们用例子来讨论一下极点：

如下图：例1

例1：讨论极点

①：我们将式子通过令分母等于0，可以得到两个极点一个为正一个为负。

②：我们通过裂项将分式裂成两个分式。

③：使用拉普拉斯的反变换可以得到时域方程

我们来对时域方程进行讨论：

​ 首先看负极点p1=-3 对应的图像是一个收敛的，随时间趋向于0的函数，是稳定的。

​ 其次看正极点P2= 2 对应的图像是一个发散的，随时间逐渐趋向于无穷大的函数，是不稳定的。

​ 那么我们将两个函数相加，可想而知系统是不稳定的。

例1简单的表现了为什么正极点会导致系统不稳定，那么如果极点是共轭负数根会是怎么样呢？我们通过一下例子再进行讨论：

如下图，例2：

例2：再次讨论极点

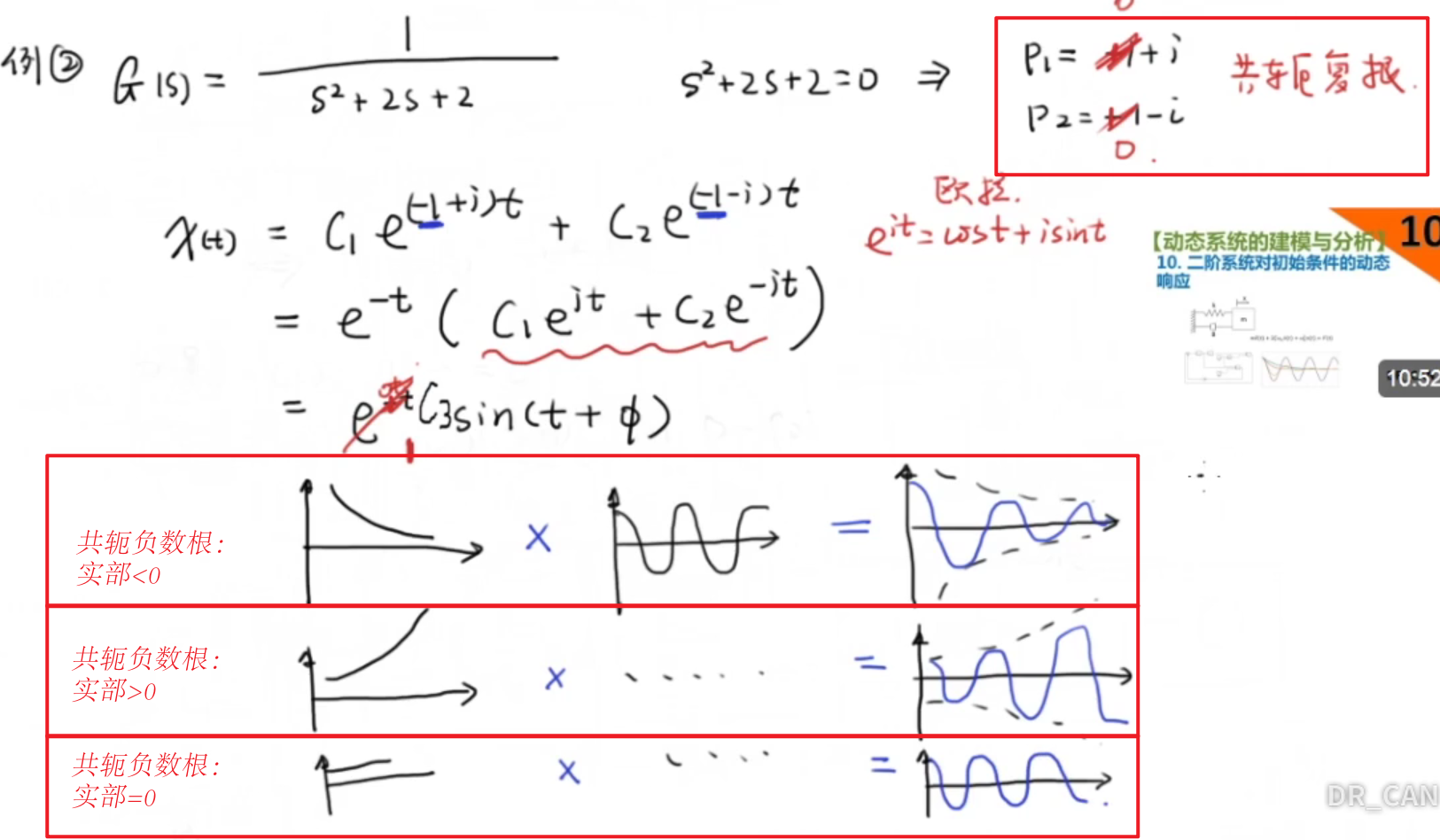
例1讨论了极点是正和负的实数情况，接下来需要讨论的是共轭复根的情况：

见上图中红色框的表。

最后总结一下极点分布对系统稳定性的影响。

图4：根的分布与系统的稳定性

‘所以想要设计一个稳定的系统，我们只需要对D控制器进行处理，使分母1+DGH的极点分布与左半平面即可。

图5：稳定系统的设计要求