写在前面
受课程的大作业启发,仔细学习了下反向传播的具体实现过程。
感谢各路大神在相关方面写的文章。
我们都知道CNN在训练时既有前向传播也有反向传播,但是在Pytorch中只需要一行代码就可以实现反向传播。 我们不必手动实现它们。 因此,大多数深度学习书籍也没有涵盖它。
文章会从卷积层、池化层、批标准化三部分进行分析。
正文
1.卷积层中的反向传播
参考了Pavithra Solai 的博客。
1.1 链式法则
开始公式推导之前我们先要了解链式法则的计算。
这部分比较基础,如果提前了解过的可以直接跳过。
我们举两个例子来做说明:
Case1
取y=g(x),z=h(y)。

当改变x时,x 会通过 g 影响 y,而当改变 y 时,y 会通过 h 影响 z。
因此,如果我们要计算 dz/dx,由于这种效应,我们可以计算 dz/dy 乘 dy/dx。
Case2
取x=g(s),y=g(s)。

然后有一个函数k,它需要x和y来得到z。 因此,对 s 进行更改会同时影响 x 和 y,从而导致 x 和 y 同时影响 z。 然后当我们计算 dz/ds 时。 我们需要计算的是 ∂ z ∂ x d x d s + ∂ z ∂ y d y d s \frac{\partial{z}}{\partial{x}}\frac{dx}{ds}+\frac{\partial{z}}{\partial{y}}\frac{dy}{ds} ∂x∂zdsdx+∂y∂zdsdy。
这就是链式法则。
现在我们提出一个简单的计算图

我们可以将 CNN 想象成这个简化的计算图。 假设我们在该计算图中有一个门 f,输入 x 和 y 输出 z。
我们可以很容易地计算局部梯度——将 z 相对于 x 和 y 的微分即为
∂
z
/
∂
x
\partial{z}/\partial{x}
∂z/∂x和
∂
z
/
∂
y
\partial{z}/\partial{y}
∂z/∂y。
对于卷积层的前向传播,输入X和F穿过卷积层,最后使用损失函数获得损失L。 当我们开始反向计算损失时,层与层之间,我们从前一层得到损失的梯度,即 ∂ L / ∂ X \partial{L}/\partial{X} ∂L/∂X和 ∂ L / ∂ F \partial{L}/\partial{F} ∂L/∂F。
1.2 前向传播
我们从前向传播开始,使用3×3输入
X
X
X 和2×2卷积核
F
F
F进行卷积以获得2×2结果
O
O
O,即如下图所示:

进行卷积的过程可以可视化如下:

基于前向传播公式,我们可以进行反向传播计算。
如上所示,我们可以找到相对于输出
O
O
O的局部梯度
∂
O
/
∂
X
∂O/∂X
∂O/∂X 和
∂
O
/
∂
F
∂O/∂F
∂O/∂F。利用前一层的损失梯度——
∂
L
/
∂
O
∂L/∂O
∂L/∂O ,并使用链式法则,我们就可以计算出
∂
L
/
∂
X
∂L /∂X
∂L/∂X 和
∂
L
/
∂
F
∂L/∂F
∂L/∂F了。
PS:为啥我们要算
∂
L
/
∂
X
∂L /∂X
∂L/∂X 和
∂
L
/
∂
F
∂L/∂F
∂L/∂F?
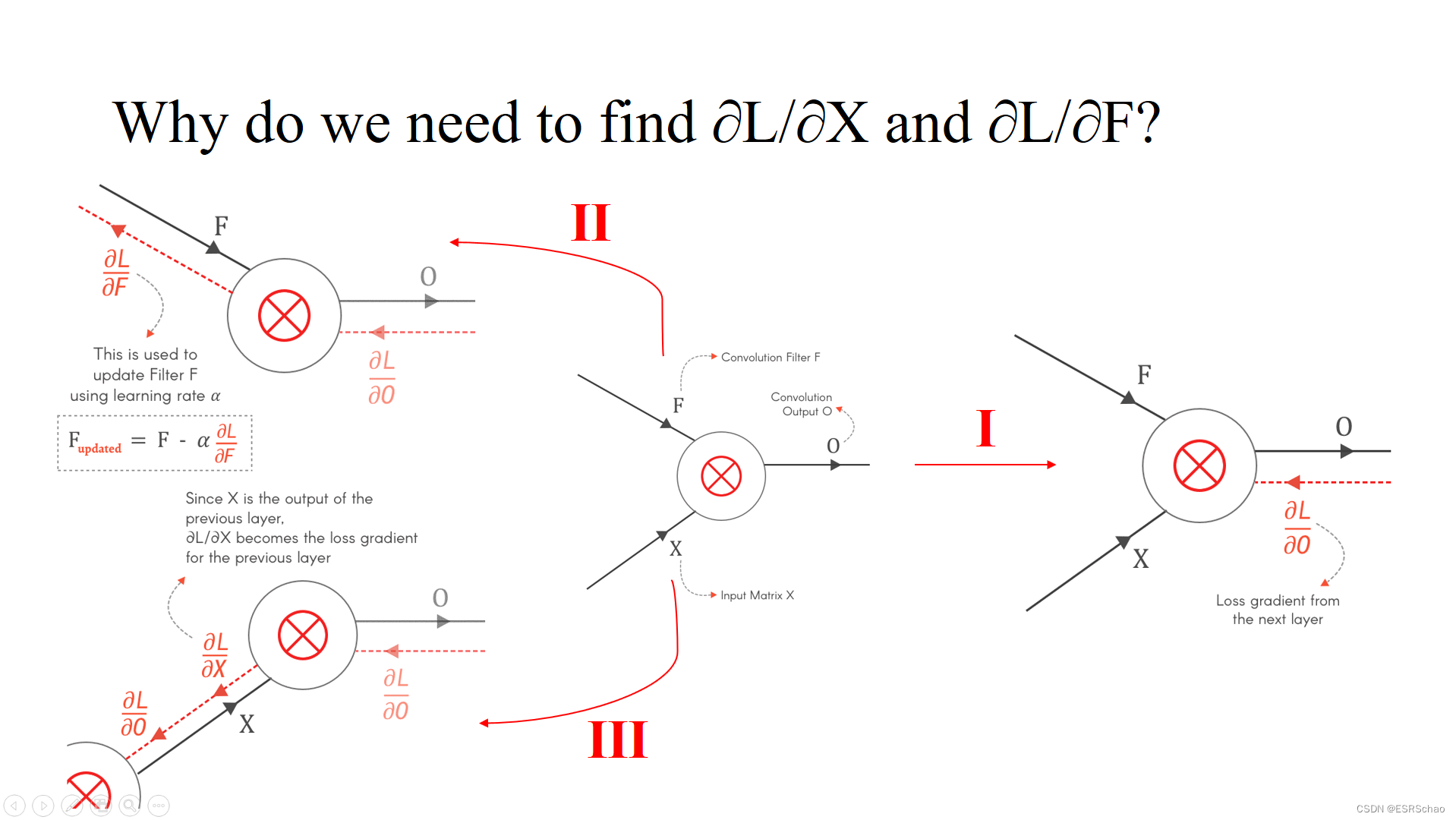
(1) 根据公式
F
u
p
d
a
t
e
d
=
F
−
α
∂
L
∂
F
F_{updated}=F-\alpha\frac{∂L}{∂F}
Fupdated=F−α∂F∂L可以看出
F
F
F是我们需要计算更新的参数,而它的更新正是通过
∂
L
/
∂
F
∂L/∂F
∂L/∂F参数来实现的。
(2)
∂
L
/
∂
X
∂L/∂X
∂L/∂X作为这一层的输入部分,在反向传播时可以看作反向传播的输出,而这个输出正是上一层的输入梯度,有了
∂
L
/
∂
X
∂L/∂X
∂L/∂X我们才能继续前一层的反向传播计算。
1.3 ∂O/∂F
第一步是局部梯度
∂
O
/
∂
F
∂O/∂F
∂O/∂F的计算

以
O
11
O_{11}
O11为例,我们只需要对
O
11
O_{11}
O11公式中对应的的
F
F
F求偏导即可。 这一步很简单。

然后使用链式法则我们可以得到
∂
L
/
∂
F
∂L/∂F
∂L/∂F,可以通过
∂
L
/
∂
O
∂L/∂O
∂L/∂O和
∂
O
/
∂
F
∂O/∂F
∂O/∂F的卷积得到。我们利用下式将其展开:

展开可以可到如下四个式子:

按照之前说的求完偏导可以得到:

可以将其表示为输入
X
X
X 和损失梯度
∂
L
/
∂
O
∂L/∂O
∂L/∂O 之间的卷积运算,如下所示。

这样我们就找到了
∂
O
/
∂
F
∂O/∂F
∂O/∂F,接下来是
∂
O
/
∂
X
∂O/∂X
∂O/∂X。
1.4 ∂O/∂X
和之前求解
∂
O
/
∂
F
∂O/∂F
∂O/∂F的过程相似,还是以
O
11
O_{11}
O11为例,这次我们需要对
O
11
O_{11}
O11公式中对应的的
X
X
X求偏导。

这样我们就得到新的梯度,利用链式法则我们可以写出新的卷积:

展开求偏导可以得到:

这9个式子乍一看没规律,但是他们依旧符合卷积的计算规则。
具体是什么规则呢,我们先将
F
F
F旋转 180 度,这可以通过先垂直翻转然后水平翻转来完成。

然后我们对它做full mode的卷积操作(卷积的几种模式的讲解可以参考这位博主的博文)。
'Full-Convolution’可以如下图可视化表示:

上面的卷积操作生成了
∂
L
/
∂
X
∂L/∂X
∂L/∂X 的值,因此我们可以将
∂
L
/
∂
X
∂L/∂X
∂L/∂X 表示如下:

现在我们已经找到了
∂
L
/
∂
X
∂L/∂X
∂L/∂X和
∂
L
/
∂
F
∂L/∂F
∂L/∂F,我们现在可以得出这个结论:
卷积层的前向传播和反向传播都是卷积。
结论可以用以下公式表示。

2.池化层中的反向传播
这部分参考了Lei Mao 大佬的博文。
由于池化层没有任何可学习的参数,因此反向传播只是上游导数的上采样操作。
这里我们拿 Max Pooling 来进行举例分析。

其中:
从Max Pooling的公式可以看出,当
x
x
x为最大值时,对输入和输出进行偏导后得到的权重
w
w
w会取1。即:

根据此公式,我们就可以得出结论:
Max Pooling的反向传播为对于非最大值没有梯度。
篇幅原因,Batch Normalization部分将在下半部分讲解。








 本文详细探讨了卷积神经网络(CNN)中卷积层和池化层的反向传播过程。通过链式法则,解释了如何计算卷积层中输入和滤波器的梯度,并展示了如何应用这些梯度来更新参数。对于池化层,特别是最大池化,说明了其反向传播仅仅是上游导数的上采样操作。此外,文章还指出卷积层的前向和反向传播本质上都是卷积操作。
本文详细探讨了卷积神经网络(CNN)中卷积层和池化层的反向传播过程。通过链式法则,解释了如何计算卷积层中输入和滤波器的梯度,并展示了如何应用这些梯度来更新参数。对于池化层,特别是最大池化,说明了其反向传播仅仅是上游导数的上采样操作。此外,文章还指出卷积层的前向和反向传播本质上都是卷积操作。


















 7140
7140

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








