Open3D的隐藏点去除算法如何实现？点云隐藏点去除算法——超详细底层算法实现讲解【深入了解算法本质】

写在前面

Open3D中的隐藏点去除算法（Hidden Point Removal）的作用是从给定视点渲染点云时，去除背景中未被其他点遮挡的点，从而提高点云的可视化效果。Open3D库中实现了[Katz2007]提出的一种基于点云可见性近似计算的隐藏点去除方法。该方法不需要进行曲面重构或法向量估计，直接利用点云数据计算点的可见性。
在使用Open3D库时我们只需要一行
_, pt_map = pcd.hidden_point_removal(camera, radius)
就可以从原始点云

得到隐藏点去除掉后的点云

但是这种算法是如何在几乎不存在点遮挡的点云中实现遮挡点去除的呢？
我找到了这篇文献Direct Visibility of Point Sets对代码的底层逻辑进行一些了解。后来有很多人在这篇文章的基础上进行了优化，但是万变不离其宗，下面就对文章的算法进行讲解。

文章解读

介绍

论文介绍了一种新的方法——直接从点云中提取可见性信息。点云是一个包含3D位置信息的采样点集，与传统的网格表示相比更加简单和灵活。通过提取点云中的可见性信息，可以实现点集的可视化、视角相关的快速重构和实时的阴影投射。本文提出的方法简单快速，不依赖于屏幕分辨率和网格拓扑结构，并且适用于各种维度的点云。另外还对算法进行了理论证明，并给出了实验结果和应用示例。

算法实现

给定一个点集 P = { p i ∣ 1 ≤ i ≤ n } ⊂ ℜ D P = \{p_{i}|1\le{i}\le{n}\}\sub{\Re^{D}} P={pi​∣1≤i≤n}⊂ℜD,这些点是在一个连续的表面$S$上采样得来的。以及一个视点$C$。我们的目标就是去找到所有在视点$C$上能看到的所有点集$P$中的点。

这种问题因为点云的稀疏性导致几乎所有点都是可见的，所以简单的直线可见性判断无法适用所有情况。所以要有新的点云可见性定义方法。如果一个点在半径为$\rho$的开放球

在数学中，一个点$p$的$r$半径开放球$B_r(p)$是指以$p$为球心，$r$为半径的球体，但不包含球体表面上的任何点。也就是说，$B_r(p)$包含所有距离$p$小于$r$的点，但不包括球体表面上的点。

内的任何位置发生微小扰动都不会被其他点遮挡，那么这个点就是可见的。
显然，可见性的合理标准必须与采样密度相关。假设$P$是平面$S$的一个$\rho -$采样，即如果我们用半径为$\rho$的开放球来围住每一个采样点$p_i$那么表面$S$将完全包含在这些球的并集内。如果在球的任何位置扰动$p_i$的位置其均不被其他点遮挡，那么$p_i$就是可见点。但是这种算法只在视线垂直于表面时有较好效果，当平面是斜面时表现不好。但是我们还要去避免计算表面法线。
为了解决这个问题，作者提出了一个名为隐藏点移除（HPR）的算子，它具有正确性、适用于倾斜曲面和合理的时间复杂度等特点。该运算符由两个步骤组成：反演(Inversion)和凸包构造(Convex Hull Construction)。

反演（点变换）

给出点集$P$和$C$,我们将$P$和一个坐标系相关联，让$C$置于原点。那么我们就需要找到一个函数将点$p_i$映射到沿着$C$到$p_i$的射线上，并在$\Vert p_i\Vert$中单调递减。其中$\Vert \cdot \Vert$是一种范数。本文介绍了名为Spherical Flipping的反演方法，它将D维球面于半径为$R$圆心在$C$的球体联系起来，这个球包含了$P$的所有点。用下式将$p_i$进行镜像反射。
$${\hat{p}}_i=f(p_i)=p_i+2(R-\Vert p_i\Vert )\frac{p_i}{\Vert p_i\Vert }$$
镜像反射的示意图如下，该公式实现了对蓝色的猫猫从绿色的球面进行镜面反射到外圈红色猫猫。

作者提示了反演函数不止这一种，像是$\tilde{f}(p_i)=\frac{p_i}{\Vert p_i\Vert \gamma }$这种公式也可以实现类似的效果。

凸包构造

点云的凸包是包含所有点的最小凸集。Open3D 包含计算点云凸包的方法。该实现基于 Qhull。使用函数compute_convex_hull就可以得到下图效果的可视化凸包：

但是这种凸包是如何构建的？
通过上一步的点变换我们可以得到变换后的点云$\hat{P}$,我们要计算的凸包是变换后的点云$\hat{P}$和中心点$C$的并集的。
文章中的主要结果就是提取了位于 P ^ ∪ { C } \hat{P}\cup\{C\} P^∪{C}凸包上的点来将其等价为可见点。这里球心$C$的引入是有必要性的，因为如果C在点云的外部时物体背面的点就会在凸包上。
我们从而可以引出一个定义：

如果点$p_i$的反射点$\widehat{p_i}$位于 P ^ ∪ { C } \hat{P}\cup\{C\} P^∪{C}的凸包上，那么点$p_i$被标记为从$C$可见。

HPR算子可以被应用于任何维度，在二维空间中更易于理解。当我们考虑一个二维点集$p_i\in P$。不失一般性，将$p_i$置于X轴上。使用极坐标系$(r,\theta )$，我们可以将$P_i$写成$p_i=(r_i,0)$。其中$r_i$是$p_i$到$C$的距离，与X轴的夹角为0。考虑穿过$\widehat{p_i}$并与X轴形成角度$\beta$的直线$\hat{L}$,如下图所示：

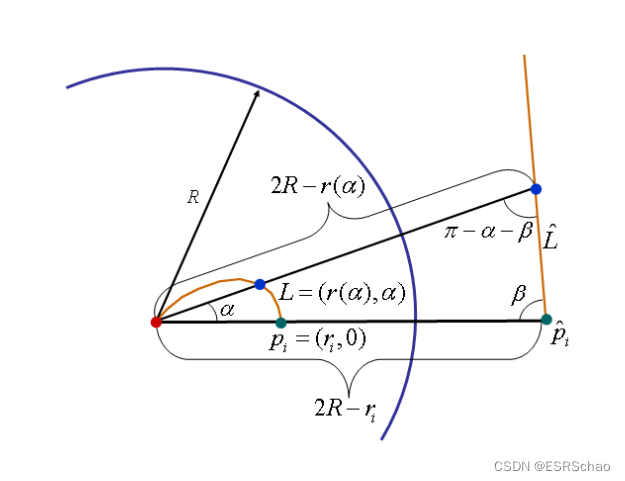
我们要找到$\hat{L}$球形翻转对应的线$L=(r(\alpha ),\alpha )$,使用正弦定理我们可以得到：
$$\frac{2R-r_i}{\sin (\pi -\alpha -\beta )}=\frac{R-r(\alpha )}{\sin \beta }$$
从而得到
$$L=(r(\alpha ),\alpha )=(2R+\frac{(r_i-2R)\sin \beta }{\sin (\alpha +\beta )},\alpha )$$
曲线$L$同时经过了$p_i$和$C$，在笛卡尔坐标系中需要用x和y的四次多项式表示。
下图说明了$L$的形状如何随着角度$\beta$的变化而变化。

$L$和X轴定义了与点$p_i$相关的空白区域。$p_i$的可见性取决于该区域的大小。该区域越大则$p_i$就越可见。HPR的重要特性就在于这个大小是由$p_i$周围的点自适应确定的，如下所述：
对于所有给定点$p_i$,$P$的两侧总存在两个特殊点$p_j$和$p_k\in P$,它们对应的曲线$L_j=(r_j({\alpha }_j),{\alpha }_j)$和$L_k=(r_k({\alpha }_k),{\alpha }_k)$,它们之间的区域就是最大可能的空白区域，如图下图所示：

当$p_i$可见时

当$p_i$不可见时

从曲线的公式可以推断出最大区域对应最小的$\beta$。这意味着对于$p_i$
而言，与最大可能空白区域相对应的${\beta }_j$和${\beta }_k$最小的。
${\beta }_j$和${\beta }_k$可以从$L$的方程里面提取出来。对于可见的$p_i$，${\beta }_j$和${\beta }_k$的和应满足${\beta }_j+{\beta }_k\le const$。
设置$const=\pi$意味着在计算上不需要为每个点找到最大化空区域大小的相邻点$p_j、p_k$了。相反，计算 P ^ ∪ { C } \hat{P}\cup\{C\} P^∪{C}的凸包就足够了。这是因为当且仅当 P ^ ∪ { C } \hat{P}\cup\{C\} P^∪{C}所有点位于由$\overline{\hat{p_i},\hat{p_j}}$和$\overline{\hat{p_i},\hat{p_k}}$定义的半空间的一侧时，点$\widehat{p_i}$才位于 P ^ ∪ { C } \hat{P}\cup\{C\} P^∪{C}的凸包上。在文中的情况下，由于$L_j$和$L_k$之间的区域是空的（图中的灰色区域），所以$\widehat{L_j}$和$\widehat{L_k}$远端的区域必须是空的。
这一观察结果在计算上很重要，也是HPR算子如此高效的原因，如果不计算凸包就必须找到$p_j$和$p_k$使算法成为二次型（在3D中甚至是三次型）。相反，如果需要做的就是计算凸包并考虑如果$\widehat{p_i}$在$\hat{P}$的凸包上时点$p_i$是可见的就可以了。因此HPR算子定义了空区域的形状和大小。
上述说明可以拓展到3D，在这种情况下空区域就不是由曲线而是由曲面定义的。此外，在3D中不是使用两个相邻点而是至少三个相邻点定义包围空体积的表面，但是这种凸包解决方法的思路是一致的。
值得注意的是，即使我们定义的$\pi$是个恒定的阈值，能见度的阈值也可以通过改变球体的半径来间接修改，$R$较大时有更大的可见范围，但在使用不同的反演函数时上述解释将保持不变但是$L$的形状会发生变化。