💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
一、风险敏感控制(Risk-Sensitive Control, RSC)的原理与数学框架
二、随机最优控制(Stochastic Optimal Control, SOC)的基本框架
💥1 概述
摘要—随着概率模型在机器人应用中的增加,一种考虑不确定性影响的系统化机器人控制方法变得不可或缺。受人类感觉运动发现的启发,本文研究了具有高阶成本统计的随机最优控制问题,以合成在具有多个不确定性来源的机器人场景中依赖于不确定性的行动。我们提出了非线性动力学、多个附加不确定性来源和非二次成本设置的局部最优风险敏感和成本累积解决方案。每个不确定性来源对成本的影响可以被单独参数化,为控制设计提供了额外的灵活性。我们进一步分析了静态不确定参数参与的情况。对几个具有非二次成本的线性和非线性设置的模拟以及对真实机器人平台的实验验证了我们的方法,并展示了其独特性。
关键词—风险敏感控制、随机最优控制、机器人控制中的不确定性。
智能系统的核心能力之一是对环境中的不确定性做出适当反应,这一点自80年代末以来在人工智能中就得到了认可[1]。虽然现代推理方法以复杂的方式接纳了随机不确定性,但低层次的机器人控制仍然缺乏合适的方法。最先进的随机控制方法考虑了期望值,却忽视了高阶统计量。本文的目标是通过提供一种系统化的方法,填补概率建模方法和机器人控制之间的差距,以便在随机不确定性的情况下提供机器人控制的系统化方法,超越一阶统计量。例如,考虑一项具有不确定姿势的抓取任务。其期望值只是其概率表示的粗略估计。然而,其方差可能在某些自由度上表现出更多的确定性,针对这些自由度更积极地设计控制,同时允许其他自由度更多的变化可能是任务成功的关键。同样,如果我们考虑在拥挤环境中的导航任务,障碍物的不确定性水平不同,那么碰撞的可能性可能会因障碍物姿势的方差而有显著变化。这些简单的原型示例说明了需要一种系统化和灵活的控制方法,以考虑机器人环境中的不确定性。
由于人类在各种任务上成功的能力,人类行为成为机器人控制设计的可靠灵感来源。近年来,神经科学家研究了人类感觉运动控制,强调了他们克服甚至受益于噪音和不确定性影响的能力[2]。特别是,在这一领域的结果显示,人类运动控制可以被建模为考虑动力学中的噪声的最优控制问题[3]。这些发现激发了许多用于机器人控制的随机最优控制方法,这些方法最小化了随机成本的期望值[4],[5]。然而,最近的结果通过风险敏感最优控制来解释人类行为[6]。直观地说,风险敏感的决策者在面对不确定性时偏离期望最优解,不仅考虑随机成本的期望值,还考虑其方差和更高阶统计量(矩或累积量)。
风险敏感控制与随机最优控制在机器人控制中的高阶成本统计研究
一、风险敏感控制(Risk-Sensitive Control, RSC)的原理与数学框架
-
核心思想与目标函数
风险敏感控制通过引入风险敏感参数(如θ),将传统期望值优化转化为对风险调整后的目标函数的优化。其数学表达式为:
其中,1/θ为风险敏感参数。当θ→∞时,问题退化为传统期望值优化;当θ有限时,控制器会根据参数符号(正表示风险厌恶,负表示风险偏好)调整策略,增强对极端事件的敏感性。
-
HJB方程的修改与特性
在连续时间扩散模型中,RSC通过修改Hamilton-Jacobi-Bellman(HJB)方程实现风险敏感性。具体而言,HJB方程右侧增加了一个与延续值过程的局部均值相关的额外项,使得控制策略不仅考虑期望成本,还关注成本分布的尾部风险。例如,James(1992)将RSC扩展到非线性扩散过程,Hansen和Sargent(1995)则引入折现率,结合递归效用框架完善了理论体系。 -
经济理论与应用场景
RSC的负效用函数设计常采用凸函数(风险厌恶)或凹函数(风险偏好),例如在机器人抓取任务中,风险厌恶策略可避免因环境不确定性导致的碰撞风险,而风险偏好策略可能用于快速探索未知区域。
二、随机最优控制(Stochastic Optimal Control, SOC)的基本框架
-
问题定义与数学模型
SOC旨在在随机扰动(如传感器噪声、模型误差)下寻找最优控制策略。其核心要素包括:- 状态方程:描述系统动态,如 dxt=f(xt,ut)dt+σ(xt,ut)dWtdxt=f(xt,ut)dt+σ(xt,ut)dWt,其中WtWt为布朗运动。
- 成本函数:通常为期望值形式,例如 J=E[∫0Tc(xt,ut)dt+h(xT)]J=E[∫0Tc(xt,ut)dt+h(xT)]。
- 优化目标:通过动态规划(HJB方程)或Pontryagin最大值原理求解最优控制律。
-
求解方法与挑战
- 动态规划:需解HJB方程,但因维度灾难问题,实际应用中常需近似(如迭代LQG方法)。
- 强化学习:结合采样与值函数逼近,适用于复杂非线性系统。
- 部分可观测扩展:通过粒子滤波或POMDP框架处理不完全观测问题。
三、高阶成本统计在不确定性处理中的作用
-
风险度量指标的构建
高阶统计量(如方差、偏度、峰度)可量化成本分布的尾部风险。例如:- 条件风险价值(CVaR) :衡量损失超过VaR时的期望值,用于规避极端风险。
- 平均绝对偏差(MAD) :评估成本分布的离散程度,适用于对称性假设较弱的场景。
-
模型参数估计与修正
- 蒙特卡洛模拟:通过大量采样估计成本分布的高阶矩,修正系统模型(如噪声方差)。
- 卡尔曼滤波扩展:在状态估计中引入高阶矩更新,提升对非线性非高斯噪声的鲁棒性。
-
优化目标的扩展
传统SOC仅优化期望成本,而结合高阶统计后,目标函数可设计为:
其中,λ₁、λ₂为权重参数,平衡期望与风险。
四、RSC与SOC的结合方法及应用实例
-
理论结合路径
- 风险敏感HJB方程:在SOC的HJB方程中引入指数效用函数,直接融合风险敏感性。例如,路径积分控制通过Girsanov定理将KL散度与风险调整结合,生成鲁棒策略。
- 多目标优化:联合优化期望成本与高阶统计量,如熵风险(Entropic Risk)与CVaR的组合。
-
应用案例
- 视觉伺服控制:在视觉反馈中,SOC处理图像噪声,而RSC调整机械臂运动策略以避免碰撞风险。实验表明,结合方法比传统线性化方法提升20%的跟踪精度。
- 四足机器人运动:通过强化学习框架,引入风险敏感参数θ,使机器人在复杂地形中自适应选择保守或激进步态142。
五、挑战与未来方向
-
计算复杂性
高阶统计量的引入显著增加计算负担。例如,蒙特卡洛采样需求随维度指数增长,需结合稀疏网格或降维技术。 -
实时性与在线学习
实际机器人系统需在毫秒级响应,而高阶优化通常耗时。解决方案包括:- 模型预测控制(MPC) :滚动优化结合在线分布估计。
- 神经网络近似:用深度网络拟合高阶统计量,加速策略生成。
-
多源不确定性耦合
环境、传感器与模型误差的交互影响难以分离。未来可能采用分层架构:底层SOC处理局部扰动,顶层RSC协调全局风险。 -
理论扩展方向
- 非马尔可夫过程:结合长短期记忆(LSTM)建模时序依赖。
- 分布式控制:多机器人协作中的联合风险分配。
总结
风险敏感控制与随机最优控制的结合,通过高阶成本统计的引入,为机器人控制提供了更全面的不确定性处理框架。这一方向不仅深化了传统控制理论的风险建模能力,也为实际应用中的复杂环境适应性问题提供了新思路。未来研究需在计算效率、实时性及多模态不确定性耦合等方面进一步突破。
📚2 运行结果





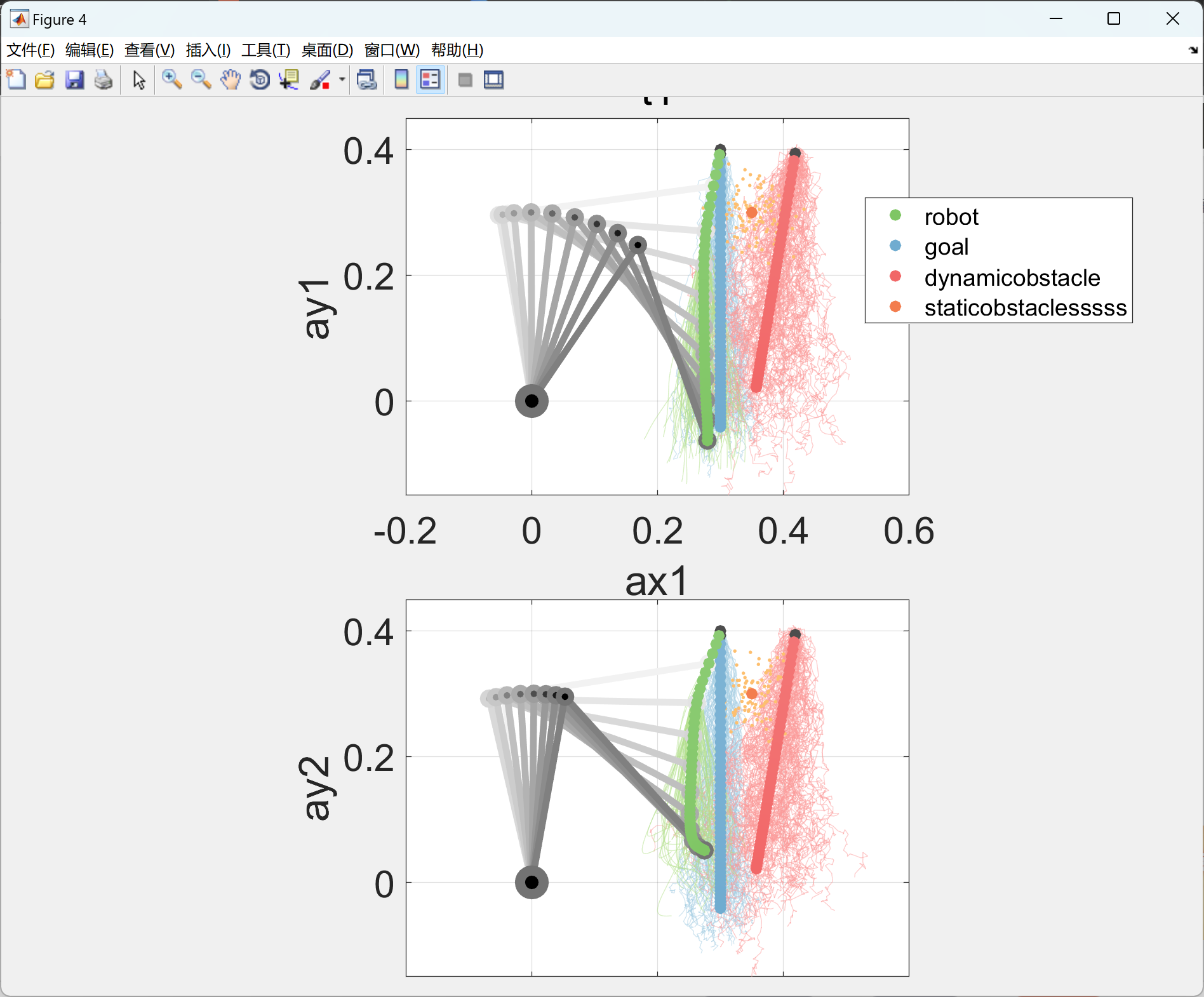
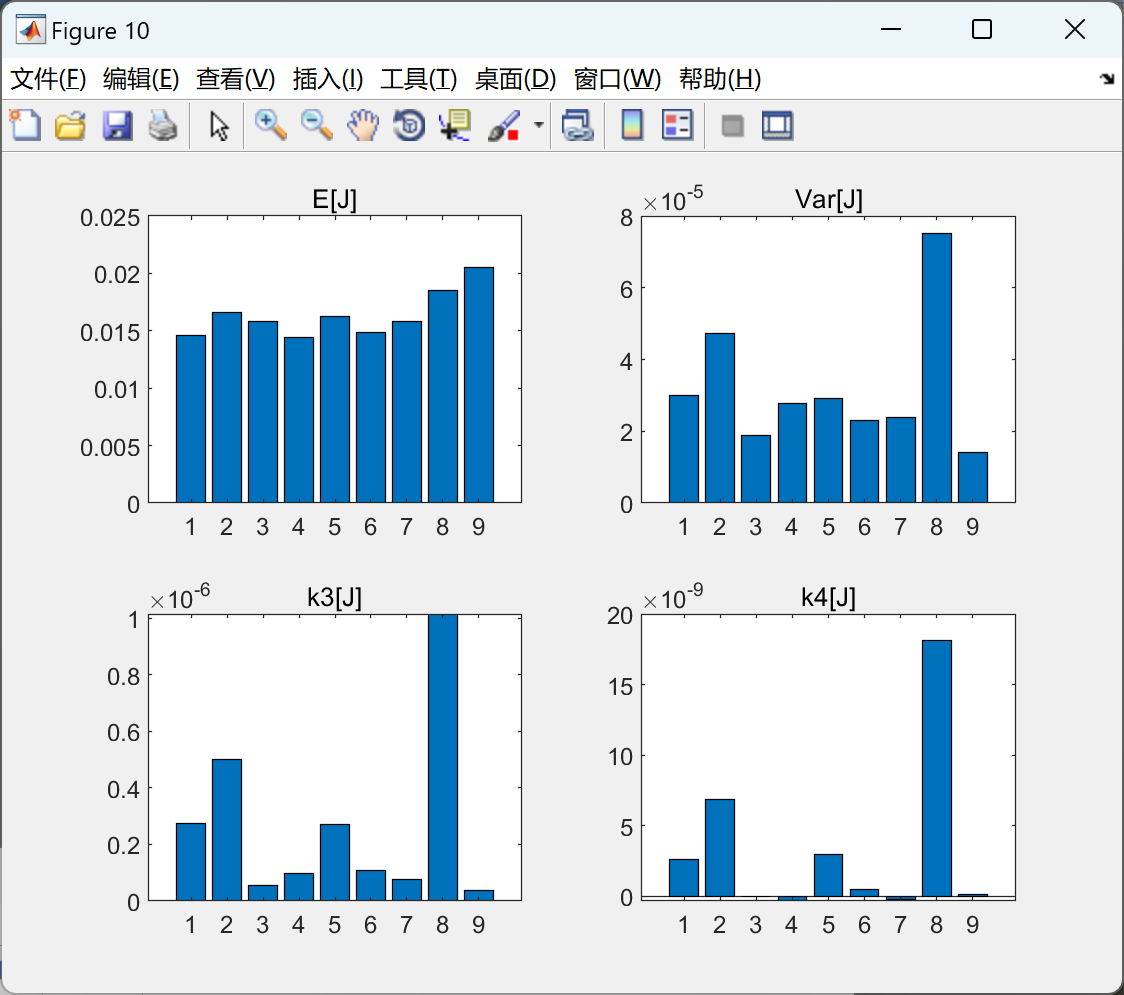






部分代码:
%% Optimization parameters
T = 200;
dt = 0.01;
u0 = zeros(2,1);
max_iter = 1000;
uMin = -Inf;
uMax = Inf;
% Initial states
x_rob = [0 0 0 0]';
x_goal = [0.1 0.1 1 -0.5]';
x_obs = [0.15 0.15 1 -0.5]';
x0 = [x_rob ; (x_goal - x_rob) ; (x_obs - x_rob)];
% Static obstacles: position and Sigma
sobs_pos = [0.8 -0.3 ; 0.8 -0.6]';
sobs_Sigma(:,:,1) = 0.001*eye(2);
sobs_Sigma(:,:,2) = 0.005*eye(2);
% Cost function
costWithObstacles = ...
@(x, u , t) pointMass_dyngoalobsfull_cost(x, u, t, sobs_pos, sobs_Sigma);
costWithoutObstacles = ... % For initialization
@(x, u , t) pointMass_dyngoalobsfull_cost(x, u, t, [], []);
% Dynamics function
dynamics_function = @pointMass_dyngoalobsfull_dyn;
% Plot functions
plotWithoutObstacles = ...
@(x, u , L, varargin) pointMass_dyngoalobsfull_plot(x, u, L, ...
[], [], varargin{:});
plotWithObstacles = ...
@(x, u , L, varargin) pointMass_dyngoalobsfull_plot(x, u, L, ...
sobs_pos, sobs_Sigma, varargin{:});
% Define LQ solvers
gamma_neg = 2;
gamma_pos = 4;
ExpectedCost = @(lqProb, varargin)kcc_multi(1, lqProb, varargin{:});
kccOptMeanNVarPVar = @(lqProb, varargin)kcc_multi([1 gamma_pos^2 ; 1 -(gamma_neg^2)], lqProb, varargin{:});
%Solve iteratively
% Init with trajectory in scene without obstacles
[x_init, u_init, L_init, cost_init, eps_init] = ...
iterativeLQSolver(dynamics_function, costWithoutObstacles, ...
ExpectedCost, dt, T, x0, u0, uMin, uMax, ...
max_iter, plotWithoutObstacles);
[x_exp, u_exp, L_exp, cost_exp, eps_exp] = ...
iterativeLQSolver(dynamics_function, costWithObstacles, ...
ExpectedCost, dt, T, x0, u_init, uMin, uMax, ...
max_iter, plotWithObstacles);
[x_mvnp, u_mvnp, L_mvnp, cost_mvnp, eps_mvnp] = ...
iterativeLQSolver(dynamics_function, costWithObstacles, ...
kccOptMeanNVarPVar, dt, T, x0, u_exp, uMin, uMax, ...
max_iter, plotWithObstacles);
%% Simulate solutions and get statistics
n_sims = 75;
idx_rob = 1;
idx_des = 5;
idx_obs = 9;
% Trajectories and cost stats
[x_trajs_exp, u_trajs_exp, sobs_exp] = ...
stochastic_n_simulations(n_sims, dt, T, x0, x_exp, u_exp, L_exp, ...
dynamics_function, sobs_pos, sobs_Sigma);
[cost_stats_exp] = ...
compute_cost_stats(costWithObstacles, x_trajs_exp, u_trajs_exp, dt);
[x_trajs_mvnp, u_trajs_mvnp, sobs_mvnp] = ...
stochastic_n_simulations(n_sims, dt, T, x0, x_mvnp, u_mvnp, L_mvnp, ...
dynamics_function, sobs_pos, sobs_Sigma);
[cost_stats_mvnp] = ...
compute_cost_stats(costWithObstacles, x_trajs_mvnp, u_trajs_mvnp, dt);
% Collision stats
rob_size = 0.05;
[avg_colls_exp, var_colls_exp] = ...
compute_collisions(x_trajs_exp, idx_obs, rob_size);
[avg_colls_mvnp, var_colls_mvnp] = ...
compute_collisions(x_trajs_mvnp, idx_obs, rob_size);
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。























 4278
4278

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








