带隙基准电路

最新推荐文章于 2025-03-10 21:28:50 发布

再世孟子

最新推荐文章于 2025-03-10 21:28:50 发布

阅读量9.2k

点赞数 27

分类专栏：模拟IC学习文章标签：经验分享

本文链接：https://blog.csdn.net/qq_46579389/article/details/127214669

版权

模拟IC学习专栏收录该内容

9 篇文章

订阅专栏

注：难得有个国庆长时间的空闲，有连续的时间学习电路知识，这次调了3个带隙基准电路（不过没绘制版图，时间上来不及），因为是初学者调的不一定好，各位懂的带佬多给点意见，嘿嘿嘿！！！

文章目录

- 1 带隙基准原理

1 带隙基准原理

1.1基本器件特性

（还不晓得囊个开个头比较好呀，还是参考几本圣经算了）
ADC、DAC、LDO等电路能够实现将模拟量转换成数字量、数字量转换成模拟量以及为后级负载提供一个相对稳定且不易改变的电源电压。这时一个能够提供几乎不随电源电压以及温度变化的基准就变得非常的重要了，他能为ADC、DAC提供一个用于参考比较的基准电压，ADC、DAC得到的实际输出值与理想的输出值的偏差很大部分就取决于带隙基准，当然LDO电路也是。

传统的带隙基准电路主要用到了采用二极管连接的三极管器件、电阻、以及MOS管构成的放大器。带隙基准的原理也就是将一个正温度系数的电压和一个负温度系数的电压按照一定的比例相加，也就得到了一个几乎不随温度变化的基准电压。所以首先来看看采用二极管连接的三极管随温度变化的特性（我这里用的sansen书上的内容，感觉对采用二极管连接的三极管特性描述这些理解推导比拉扎维理解深一点）。（下面内容对二极管连接的三极管全部统称为二极管算了，然后为啥采用二极管连接的三极管而不直接采用二极管sansen书上给出的解释是二级管的电流电压关系在热电压KT/q前面有个1.05~1.1的系数，但是采用二极管连接的三极管却咩有。）
![在这里插入图片描述](https://img-blog.csdnimg.cn/adfad460c53a4f598478179308abdb69.png

一般我们可以用指数关系描述二极管的电流和电压的关系即公式1（别去纠结为啥少了模电书上那个1，热电压才26mV，VBE一般都是600mV往上，后面那个1完全可以忽略，我算了哈指数项在VBE=600mV的电压下值为10^10量级。），当考虑温度影响时可以用公式2描述，也就是说前面的系数项Is也会受到温度的影响。这里就有三个变量了，Ic、T、VBE。我们同时也想了解温度对VBE的影响，三个变量这种情况我们采用高中就学过的控制变量法，将Ic保持不变，可以得到VBE随温度的变化，也就是公式3，其中每个项的定义可以在下面的图中看到。（下图中λ约为2mV/℃，sansen，拉扎维，Allen三本书给出的各不相同，分别是2mV/℃，1.5mV/℃，2.2mV/℃）
在这里插入图片描述
最终其实可以写成下面这个公式：（这里我们可以看到VBE和温度的关系其实是一个一阶项加一个lnT有关的项）
$V_{\mathrm{BE}}(T)=V_{\mathrm{g0}}-\left(V_{\mathrm{g0}}-V_{\mathrm{BE(Tr)}}\right) \frac{T}{T_r}-(\eta-m) V_T \ln \frac{T}{T_r}$
需要记住：

$V_{g0} = 1156mV$
$V_{BE}(T_r) = 700mV$
$T_r = 300K$
η约等于4，对于恒定的电流m约为0，而对于一个PTAT（正比于温度的电流）电流m约为1，（记住这个结论等会对带隙基准的高阶曲率进行补偿时会用到。）

1.2 如何得到正温度系数和负温度系数的量（输出为1.21V左右的带隙基准）

负温度系数的量：
刚才我们看到VBE已经是一个与温度负相关的量了，不考虑高阶项VBE基本上是一个与温度成一阶关系的量，这里我们就得到了一个负温度系数的量，当然前提是能够得到一个恒定的电流或者PTAT电流。
在这里插入图片描述
正温度系数（抄一手拉扎维书）：
1964年人们就认识到，如果两个BJT工作在不相等的电流下，那么他们的基极发射极电压的差值就与绝对温度成正比。

上图采用了两个相同的晶体管，但是两边加的电流有一个比例n。同样的加相同的电流改变二极管的比例可以得到同样的正温度系数的电压。如下图：
在这里插入图片描述
现在我们还存在两个问题：

恒定的电流或者PTAT电流如何生成如何生成
如何将两个电压相加

再分析分析上面这个图，X和Y点差一个热电压×lnn。不管如何改变电流XY点的电压差都不变，这里如果我们在Y点加上一个电阻R，使得其电流流过电阻产生的压降等于压差，但是再次注意到电流是恒定的，电流在电阻上的压降也为恒定的，如果把电流变成PTAT的电流，那么就有可能使得XY两端电压相等，换句话说如果我们使得XY两点的电压相等我们就得到了一个PTAT电流，并且这个电流等于 $V_Tln(n)/R$ 。这里就将正温度系数的电压转变成了电流。这样我们就可以通过VBE和这个生成的PTAT电流构造几乎与温度无关的电压了。（如何使得XY点的电压相等，我们注意到理想运放虚短原理，即理想运放的两个输入端口可以视为电压相等）
在这里插入图片描述

1.3 三个带隙基准的原理

1.3.1 输出1.21V的带隙基准

这里直接参考的李福乐老师的图。
在这里插入图片描述
输出电压可以表示为：
$\begin{aligned} V_{\text {tult }} &=V_{\mathrm{BE} 2}+\frac{V_T \ln n}{R_0}\left(R_0+R_2\right) \\ &=V_{\mathrm{BE} 2}+\left(V_T \ln n\right)\left(1+\frac{R_2}{R_0}\right) \end{aligned}$

1.3.2 电流模式的带隙基准（低压带隙基准）

在这里插入图片描述
之前提到，只要使得XY点的电压相等也就产生了PTAT电流，此时再次查看XY点的电压变化情况，这里的电压会随着VBE的电压变化而变化，那么在XY点分别接入一个电阻，那么就可以产生一个负温度系数的电流，同样的通过调整电阻的比例可以得到温度系数较小的恒定电流，再将这个电流通过电流镜复制到另外一个支路，通过电阻，也就可以得到我们想要的一个低压带隙基准了。

$V_{\mathrm{BG}}=\frac{R_4}{R_2}\left(\left|V_{\mathrm{BE} 1}\right|+\frac{R_2}{R_1} V_T \ln n\right)$
上述推到未考虑电阻随温度的变化特性，但是我们还是可以从公式中看到，最终电阻全部在分子或者分母，可以将电阻的温度特性抵消掉（当然还得记住这只是理论推导，实际上我们还是希望电阻的变化尽可能的小）。

1.3.3 带曲率校正的带隙基准

之前我们提到，在恒定的电流下，二极管的电压VBE可以写成：
$V_{\mathrm{BE}}(T)=V_{\mathrm{g0}}-\left(V_{\mathrm{g0}}-V_{\mathrm{BE(Tr)}}\right) \frac{T}{T_r}-(\eta-m) V_T \ln \frac{T}{T_r}$
并且有：η约等于4，对于恒定的电流m约为0，而对于一个PTAT（正比于温度的电流）电流m约为1

刚才通过将一个正温度系数电压/电流和一个负温度系数电压/电流按一定的比例相加得到了温度系数较小的电压/电流，同样的思路，通过一定的方式VBE后面的高阶项（lnT/Tr）给提取出来，叠加到刚才得到的量上，那么就可以得到一个补偿掉ln(T/Tr)的基准。
在这里插入图片描述
（这里直接截的论文原图）Q1Q2上的电流为PTAT电流，Q3上的电流为温度系数较小的电流，那么就可以发现Q1与Q3上的电压有个差值，这个差值为：
$V_{N L} \cong V_{\mathrm{BE}, Q_3}(T)-V_{\mathrm{BE}, Q_{1,2}}(T)=V_T \ln \frac{T}{T_0}$
进一步可以得到：
$\begin{aligned} V_{\text {out }} &=V_T\left(\frac{R_3 \ln (N)}{R_0}\right)+V_{\mathrm{BE}}\left(\frac{R_3}{R_1}\right)+V_{N L}\left(\frac{R_3}{R_{4,5}}\right) \\ &=\frac{R_3}{R_1}\left(\frac{R_1 \ln (N)}{R_0} V_T+V_{\mathrm{BE}}+\frac{R_1}{R_{4,5}} V_{N L}\right) \end{aligned}$

2.失配和速度以及噪声的问题

2.1失配：

首先看看MOS管随机失配的影响：
$\begin{gathered} \Delta V_{\mathrm{TH}}=\frac{A_{\mathrm{VTH}}}{\sqrt{W L}} \\ \Delta\left(\mu C_{\text {ox }} \frac{W}{L}\right)=\frac{A_K}{\sqrt{W L}} \end{gathered}$
对做输入差分管的MOSFET有：（这里截图为National Semiconductor的一个pdf，之前在eetop上找到的，这里理解也比较简单，对差分对，我们的目的就是使得两个差分对通过的电流相等，直接求全微分，得到Vgs与Vt还有β的关系，β=μCoxW/L）
在这里插入图片描述
所以对与输入差分对我们要取小的这个过驱动电压，或者说大的gmoverId值，即往亚阈值区那个方向取。
对电流镜有（这里由于Vgs相等，看的是电流随β和Vt偏差的变化，所以同样直接求导，得出Id与其他量的函数）：
在这里插入图片描述
最后可以得到对电流镜要取大的过驱动电压，小的gmoverId值。
然后还有BJT的偏差（来自sansen书上，这里是做差分输入管推导出来的）：

这里我们可以看到BJT的偏差相对于MOSFET小很多（KT/q的值比(Vgs-Vt)/2小得多），也就是说在CMOS工艺中的带隙基准由BJT导致的Vos占比很小（拉扎维书上直接没有考虑BJT的偏差，只考虑了运放的偏差）。
失配影响（这里图来自一个大佬的博客，博客链接在最下面的部分）：
在这里插入图片描述

2.2 速度和噪声的问题

这里主要讲的问题还是带隙基准不能通过miller补偿来实现环路的稳定性，主要的原因就是miller补偿添加的大电容很容易就将对应管子gate端的变化耦合到drain端，具体还是参考拉扎维书上的分析：
在这里插入图片描述

emmmm 环路稳定性问题不想扯了，不过提醒哈二极管连接的BJT的等效电阻的推导。

在这里插入图片描述

当初上模电的老师说Rb一般为300Ω，还有个β的问题，一般来说贝塔都是几十往上走的，不过CMOS工艺中的BJT我仿真了一哈只有β≈2。不过对你推导影响不大的。

3 带隙基准

3.1 输出1.21V左右的带隙基准

（我也没搞成symbol然后再建立原理图做测试，主要是我懒）
在这里插入图片描述

运放采用了折叠式共源共栅结构，为了尽可能的减小失配把输入差分管压到了亚阈值区去，而NMOS电流镜那里直接搞成了倒比管（W/L=1：2），主要是为了提高过驱动电压尽可能的减小失配。然后为了减小失配还在source端加了电阻（不大7K左右），这玩意叫源极退化技术。
然后是电阻的选取，前面提到虽然公式上的确是把对应电阻的温度系数抵消了，但实际上还是希望有温度系数小的电阻。所以这里采用了p参杂的poly电阻（rpposab_3t_ckt电阻），为啥要采用这个电阻看下面的图（可以说这个电阻不仅相对误差比较小，同时还有非常小的温度系数）（图片来自我用的工艺库的pdf文档），然后还要注意为了版图好画好做匹配（虽然我并没有画版图），我们需要用一个宽度和长度固定的电阻作为参考电阻，其他的需要的电阻值通过多个参考电阻的串联或者并联得到。
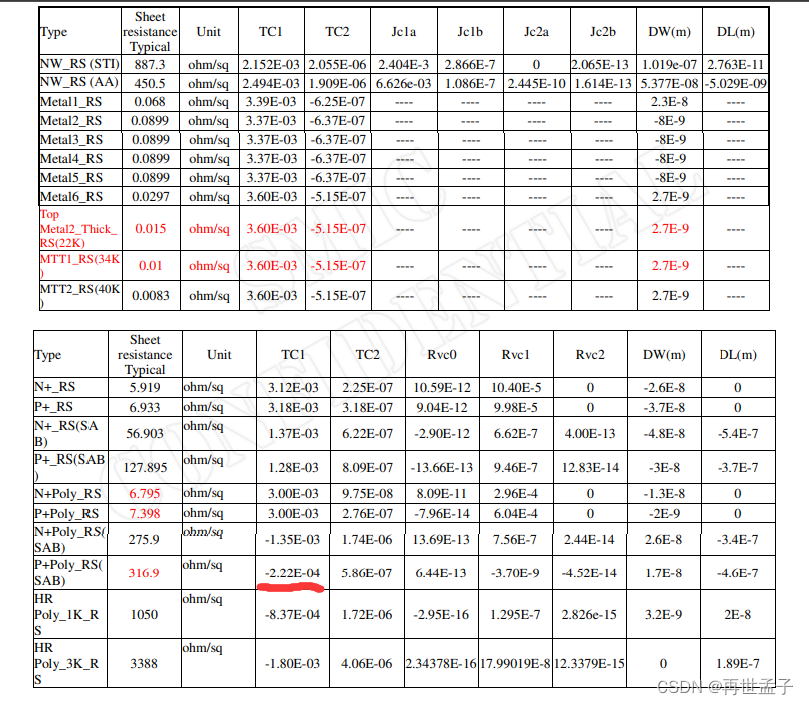
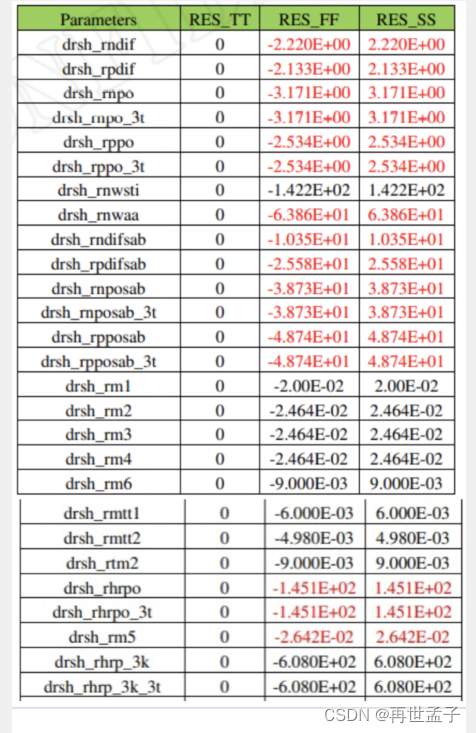
启动电路，emmmm我就用了之前看到的一篇论文上面的启动电路，不过现在这个电路在2V的时候启动似乎有点问题，不过电压大点问题不大。
最后上面的电流镜那一块我也没搞cascode，加了cascode能够一定程度上提高PSRR。

然后是调出来的效果

先看TT corner下的温度温度曲线吧：
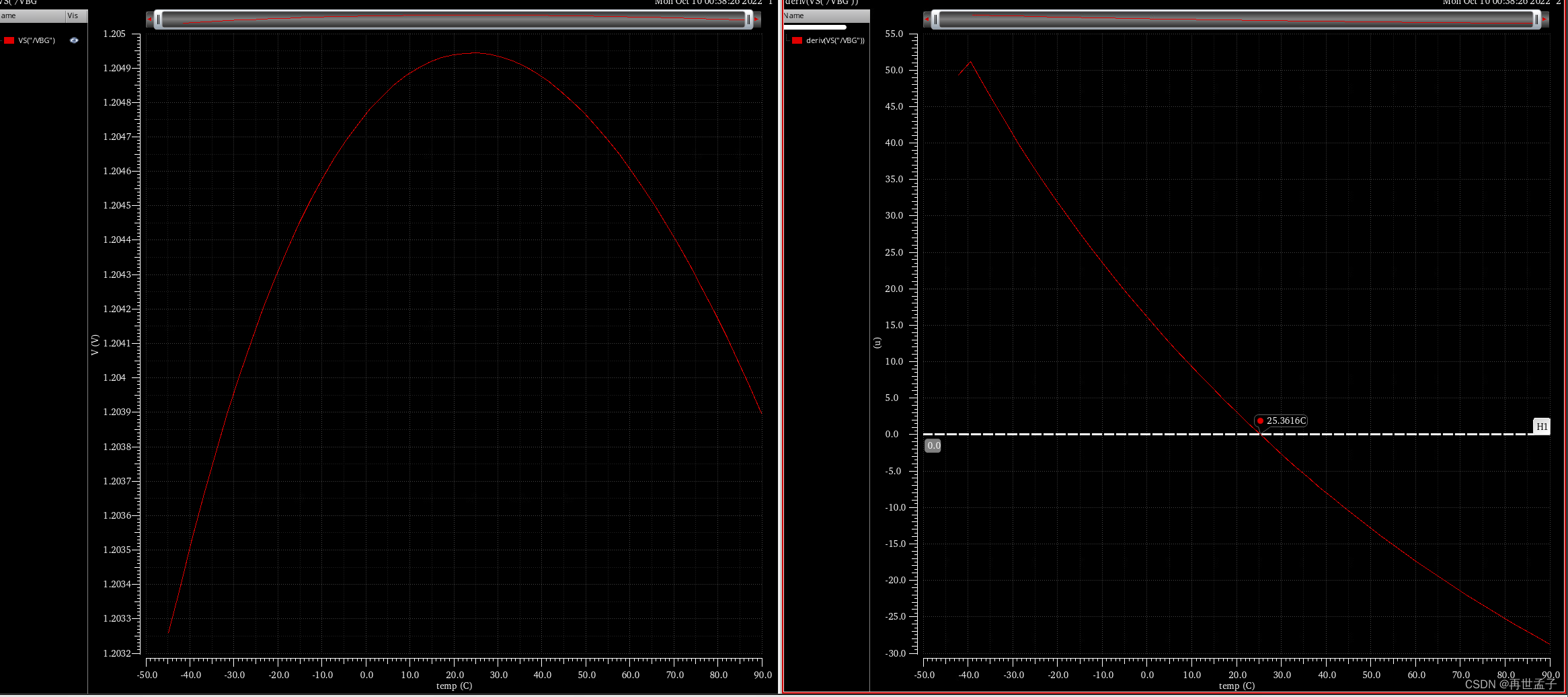
然后是环路稳定性（tt corner其他工艺角没看，也是懒）：
噪声（tt corner）：
* PSRR（tt corner 没搞失配后的psrr）
终于到了我调了快一天才搞好的offset（2%左右 3σ），还有温度系数：

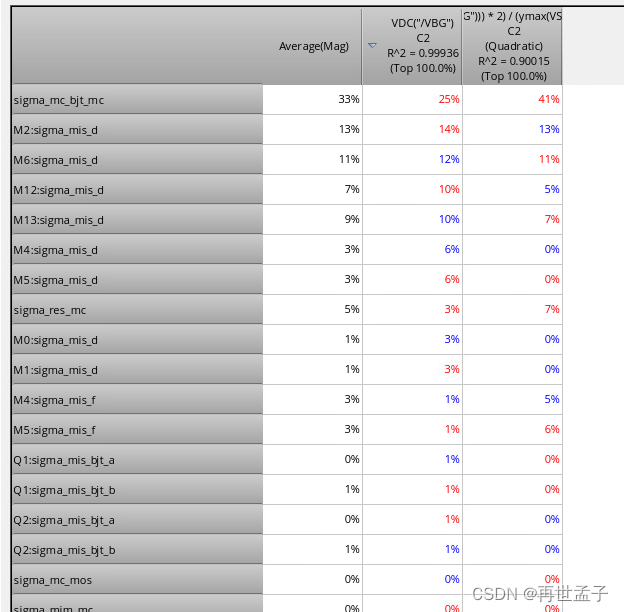
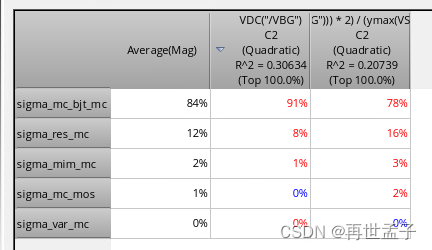
所以我这还想继续减小可得改BJT的参数了（BJT我用的最小那个2x2的）。

3.2 电流模式带隙基准

在这里插入图片描述

不得不说电压低了过后的带隙基准启动电路是真的不好搞。
这个启动电路在1.5V电源电压的时候启动时间还花得挺久的。
同时失调也比上面那个还难调。

3.3 高阶补偿的带隙基准

在这里插入图片描述

这个东西就只有tt corner下的那个输出电压随温度系数的曲线比较小，其工艺角感觉不行，我看原文论文都是用了可编程的电阻网络来修调，而且这玩意只是在tt corner下就很难调。（我就只调得到下面这个样子了，调不动了，太费时间，躺平开摆）

附录

参考过的东西：
1.https://blog.csdn.net/u010486560/article/details/116420117?spm=1001.2014.3001.5502 （刚才那个博客）
2.论文：Curvature-Compensated BiCMOS Bandgap with 1-V Supply Voltage
3.李福乐老师的 bandgap and LDO
4.Random Offest in CMOS IC Design（个人感觉这个文档讲得挺好，eetop上下得到）
在这里插入图片描述
5.拉扎维书、sansen书、Allen书对应章节。