损失函数——论文翻译

论文的讲解可转站视频：

夏日的盒盒的个人空间-夏日的盒盒个人主页-哔哩哔哩视频 (bilibili.com)

摘要

       大多数最先进的机器学习技术都围绕着损失函数的优化。因此，定义适当的损失函数对于成功解决该领域的问题至关重要。我们对各种不同应用中最常用的损失函数进行了调查，分为分类、回归、排序、样本生成和基于能量的建模。总体而言，我们引入了 33 个不同的损失函数，我们将它们组织成一个直观的分类法。每个损失函数都被赋予一个理论上的备份，我们描述了它的最佳使用位置。本调查旨在参考初学者和高级机器学习从业者最基本的损失函数。

附加关键词和短语：损失函数、机器学习、神经网络、调查

一、介绍

       在过去的几十年里，人们对机器学习的兴趣激增。该领域侧重于可以在数据上训练的算法的定义和应用，以模拟底层模式。机器学习方法可以应用于许多不同的研究领域，包括生物医学科学、自然语言理解异常检测、图像分类、数据库知识发现、机器人学习、在线广告、时间序列预测、脑计算机接口等。为了训练这些算法，有必要定义一个目标函数，该函数给出了算法的性能的标量度量。然后可以通过优化目标函数的值来训练它们。

       在机器学习文献中，这样的目标函数通常以损失函数的形式定义，当损失函数最小化时是最优的。损失函数的确切形式取决于要解决的问题的性质、可用数据和正在优化的机器学习算法的类型。因此，找到合适的损失函数是机器学习中最重要的研究工作之一。

       随着机器学习领域的发展，人们提出了许多不同的损失函数。因此，总结和理解它们非常有用。然而，很少有作品试图对整个领域进行此操作。文献中损失函数的现有评论要么缺乏对结构和上下文化不同损失的良好分类，要么特别关注机器学习应用程序的特定子集。也没有一个单一的源将最常用的损失函数放在相同的正式设置中，列出每个损失函数的优缺点。

       出于这个原因，我们致力于构建损失函数的适当分类，我们展示了每种技术的优缺点。我们希望这对于希望熟悉机器学习文献中使用最常见的损失函数的新用户很有用，并发现适合他们试图解决的问题的用户。我们还希望这个摘要将作为高级用户的综合参考有用，使它们能够快速找到最佳损失函数，而无需广泛搜索文献。此外，这可以帮助研究人员找到进一步研究的可能途径，或者了解在哪里放置他们提出的任何新技术。例如，他们可以使用这项调查来了解他们的新建议是否符合我们提出的分类，或者他们是否属于一个全新的类别，也许以新颖的方式结合不同的想法。

       总的来说，我们包含了33个最广泛使用的损失函数。在这项工作的每个部分中，我们根据它们可以用于的任务的广泛分类来分解损失。每个损失函数将被数学定义，并列出其最常见的应用突出的优点和缺点。

       这项工作的主要贡献可以在图1所示的拟议分类法中找到。每个损失函数首先根据它们所利用的具体任务进行划分:回归、分类、排序、样本生成和基于能量的建模。此外，我们根据它们可以应用的学习范式类型对它们进行划分，从有监督到无监督。最后，我们根据它们所基于的基本策略对它们进行分类，例如它们是否依赖于概率形式化，或者基于误差或预测值与实际值之间的范围。

       这项工作的组织如下：在第 2 节中，我们提供了损失函数的正式定义并介绍了我们的分类法。在第 3 节中，我们描述了用于降低模型复杂性的最常见的正则化方法。在第 4 节中，我们描述了用于训练回归模型的回归任务和关键损失函数。在第 5 节中，我们介绍了分类问题和相关损失函数。在第 6 节中，我们介绍了生成模型及其损失。第7节介绍了排序问题及其损失函数，第8节描述了基于能量的模型及其损失。最后，我们在第9节中得出结论。

二、损失函数分类的定义

       在一般的机器学习问题中，目标是学习一个函数 f，该函数将输入（由输入空间 Φ 定义）转换为所需的输出，由输出空间 Y 定义：

𝑓 : Φ → Y

其中 f 是一个函数，可以用模型 fΘ 近似，由参数Θ 参数化。

      给定一组输入 {x0,..., xN } ∈ Φ，它们用于训练模型，参考输出空间中的目标变量 {y0,..., yN } ∈ Y。请注意，在某些情况下（例如自动编码器）Y = Φ。

      损失函数L被定义为f(xi)与其对应的 yi 到实数 l∈R的映射，它捕获了f(xi)和yi之间的相似性。聚合数据集的所有点，我们发现整体损失 L：

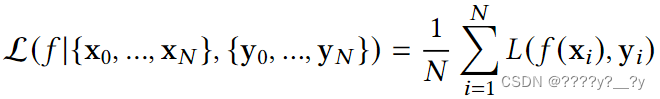
要解决的优化函数定义为：

       请注意，通常很方便地引入正则化项 (R)，它将 f 映射到实数 r ∈ R。该术语通常用于惩罚优化中模型的复杂性：

       在实践中，为优化选择的函数族可以通过参数向量 Θ 参数化，这允许最小化定义为参数空间的探索： 

2.1损失函数优化技术 

2.1.1损失函数和优化方法

       在本节中，我们列出了损失可能或可能不满足的最常见的数学属性，然后简要讨论了用于最小化它们的主要优化方法。为简单起见，可视化和理解我们在二维空间中定义了这些属性，但它们可以很容易地推广到 d 维属性。

       •连续性(CONT):实数函数，即从实数到实数的函数，可以用笛卡尔平面上的图表示;如果图是属于实域的一条不间断曲线，则函数是连续的。通过用极限来定义连续性，可以给出一个更严格的数学定义。变量变量的函数𝑓在实数𝑐处是连续的，条件是lim(1)→𝑐𝑓(1)=𝑓(𝑐)。
       •可微性(DIFF):在实变量上的可微函数𝑓是在其定义域的每一点上可导的函数。可微函数是光滑的(函数在每个内部点上都是局部近似为线性函数)，并且不包含任何断点、角度或尖角。连续函数不一定是可微的，但可微函数一定是连续的。
       •Lipschitz连续性(L-CONT): Lipschitz连续函数的变化速度有限。更正式地说，存在一个实数，使得对于函数图上的每一对点，连接它们的直线斜率的绝对值不大于这个实数;这个值称为函数的李普希茨常数。为了理解模型(如神经网络)的鲁棒性，一些研究论文试图通过定义一个具有小Lipschitz常数的输入-输出映射来训练底层模型。直觉是，如果一个模型是鲁棒的，那么它不应该太受输入中的扰动的影响，𝑓(𝑥+𝛿𝑥)≈𝑓(𝑥)，并且可以通过𝑓为ℓ-Lipschitz来确保这一点，其中ℓ很小。

       •凸性(CONV):一个实值函数𝑓是凸的，如果函数图上任意两点之间的每个线段都在两点之间的图上。凸性是一个重要的特征，因为凸函数的局部极小值也是全局极小值。当一个函数的二阶导数存在时，它的凸性很容易检验，因为函数的Hessian一定是正半定的。
              •严格凸性(Strict Convexity, S-CONV):一个实值函数是严格凸的，如果函数图上任意两点之间的线段位于两点之间的图形之上，直线与曲线的交点除外。严格凸函数有一个正的确定Hessian。正定矩阵是可逆的，优化问题可以用封闭形式求解。

2.1.2相关优化方法

       优化方法是一种技术，给定一个目标函数的形式化优化问题，返回解以获得该优化问题的最优值。这项工作中提出的大多数优化方法都依赖于可能无法保证解最优性的算法，但暗示了一定程度的近似。

       •封闭形式的解决方案是方程组，可以通过找到Θ的值来解析解决，该值导致损失函数的导数为零值。如果目标函数对Θ可微且对Θ可微，则优化问题是闭型可解的。一般情况下，求闭形式解需要可微性和严格凸性。如果封闭形式的解决方案是可用的并且在计算上是可行的，那么应该总是使用它们来代替迭代算法。
       •梯度下降是一种一阶迭代优化算法，用于寻找可微函数的局部最小值。该过程在与当前点的函数梯度相反的方向上重复步骤，其步长由参数𝛼定义，通常称为学习率。所使用的损失函数必须是可微的，这样才能计算出梯度。为了克服这一限制并使用不可微损失函数，可以使用梯度逼近和其他技术。算法1对梯度下降过程进行了形式化描述。
       •随机梯度下降(SGD)是梯度下降优化的随机近似。它用一个估计值取代了从整个数据集中计算出来的实际梯度，这个估计值是从随机选择的数据子集中计算出来的。随机梯度是真实梯度的无偏估计。在高维优化问题中，例如在人工神经网络中，这减少了时间成本。这种方法的随机性降低了优化陷入局部最小值的概率。SGD具有与传统梯度下降相同的约束条件(即可微性、最优解的凸性)。
       •无导数优化在某些情况下，目标函数的导数可能不存在，或者可能不容易计算。这就是无导数优化发挥作用的地方。经典的模拟退火算法、遗传算法和粒子群优化算法就是这样的例子。传统的无导数优化方法通常难以扩展到大规模问题。要了解有关无导数优化的更多信息，您可以参考。
零阶优化(ZOO)是无梯度优化的一个子集，出现在各种信号处理和机器学习应用中。ZOO优化方法是一阶优化技术的无梯度对应。ZOO通过基于函数值的梯度估计近似全梯度或随机梯度。最近一些重要的应用包括在深度神经网络上生成预测规避、黑盒对抗攻击，从机器学习系统生成模型不确定的解释，以及以计算效率高的方式设计梯度或曲率正则化鲁棒ML系统。与传统的无导数优化方法相比，零优化可以是一个方便的选择，因为它很容易在常用的基于梯度的算法(例如SGD)中实现，它有效地近似导数，并且具有与一阶算法相当的收敛速度。

2.2我们的分类 

       我们的分类方法总结在图1中。为了定义它，我们首先根据最适合解决的机器学习问题对损失进行分类。我们确定了以下类别:
回归(第4节)
       •分类(第5节)
       •生成模型(第6节)
       •排名(第7部分)
       •基于能源的建模(第8节)
 我们还根据用于定义损失的数学概念进行了区分，获得了以下子类别:
       •基于偏差
       •基于概率
       •基于边界
       利用这种方法，发现了一个紧凑和直观的分类法，不同部分之间几乎没有冗余或重叠。我们使用了众所周知的术语来定义分类法，这将使任何用户都更容易直观地理解它。

三、正则化方法

       正则化方法可以应用于几乎所有的损失函数。它们被用来降低模型的复杂性，简化训练模型，减少训练数据的过拟合倾向。模型的复杂性，通常是通过参数的数量及其大小来衡量的。有许多技术属于正则化方法的范畴，其中很大一部分是基于损失函数的增广。正则化的一个直观的理由是，它将奥卡姆剃刀强加于最终模型的复杂性上。从理论上讲，许多基于损失的正则化技术相当于在模型参数上施加某些先验分布。

3.1损失增强正则化

       人们可以设计损失函数来惩罚模型参数的大小，从而学习模型的偏差和方差之间的最佳权衡，并在不影响训练误差的情况下减少泛化误差。这可以防止过度拟合，同时避免欠拟合，并且可以通过使用显式控制参数大小的术语来增强损失函数来完成，或者隐含地减少它们的数量。增强损失函数以正则化结果的一般方式在下面的等式中形式化：

其中𝜌(Θ)被称为正则化函数，并定义了正则化的量(拟合和泛化之间的权衡)。这个一般定义清楚地表明，我们可以对本文提出的任何损失使用正则化。我们现在将描述基于损失增强的最常见的正则化方法。

3.1.1 L2 范数正则化。

       在𝐿2正则化中，损失被增强以包含权重的加权𝐿2范数[12,77]，因此正则化函数为：

当这被用于回归问题时，它也被称为岭回归。 

3.1.2 L1 范数正则化

       在L1正则化中，损失被扩充以包括权重的加权L1范数，因此正则化函数是：

当这被用于回归问题时，它也被称为Lasso回归 。

3.2 L2和L1范数正则化之间的比较

       𝐿1和𝐿2正则化都基于对组成模型的权重的大小进行惩罚的相同概念。尽管如此，这两种方法在就业能力和对结果的影响方面存在重要差异。
       最关键的区别之一是，𝐿1经过优化后，能够将权重缩小到0，而𝐿2的结果是非零(平滑)值。这允许  𝐿1降低模型参数空间的维度并执行隐式特征选择。事实上，已经有论文表明，通过在逻辑回归上使用𝐿1正则化，样本复杂性(即“学好”所需的训练样例的数量)在不相关特征的数量上呈对数增长。相反，作者表明，任何具有𝐿2正则化的旋转不变算法(包括逻辑回归)在最坏情况下，样本复杂性在不相关特征的数量上至少呈线性增长。此外，𝐿2比𝐿1-norm对异常值更敏感，因为它对误差进行了平方。
       𝐿2是连续的，而𝐿1是分段函数。𝐿2的主要优点是它是可微的，而𝐿1在0处是不可微的，这有一些很强的含义。准确地说，𝐿2范数可以很容易地用梯度下降训练，而𝐿1范数有时不能有效地应用。第一个问题是对所有特征的权重应用𝐿1惩罚的效率低下，特别是当特征空间的维度往往非常大时，会导致权重更新过程的显著减慢。最后，在SGD中幼稚地应用𝐿1惩罚并不总是导致紧凑的模型，因为每次更新时使用的近似梯度可能非常嘈杂，因此这些波动很容易使特征的权重远离零，并且𝐿1相对于𝐿2失去了它的主要优势。

四、回归损失

       回归模型的目的是基于一个或多个预测变量x(自变量)的值来预测连续变量(因变量)的结果。更准确地说，设𝑓Θ是一个由Θ参数化的通用模型，它映射自变量x∈{x0，…， x <s:1>∈R𝐷，x}， x∈R𝐷到因变量∈R。最终的目标是通过最小化损失函数𝐿来估计最接近拟合数据的模型Θ的参数。
       回归任务所考虑的所有损失都是基于残差的函数，即观测值和预测值之间的差值𝑓(x)。下面，设𝑓(x)为对x的预测结果，而草本为感兴趣的变量的基本真值𝑡(x)。
       如图2所示，平均偏差误差(𝑀𝐵𝐸)损失可以被认为是回归损失的基本支柱，其特征是有许多变化。其中最相关的是:平均绝对误差(𝑀𝐴𝐸)、均方误差((𝑀𝑆𝐸)和均方根误差(𝑅𝑀𝑆𝐸)损失。在本节中，我们还将介绍Huber损失和平滑L1，它们是𝑀𝐴𝐸和𝑀𝑆𝐸之间的混合。最后，给出了Log-cosh和均方根对数误差损失。

4.0.1 平均偏差误差损失 (CONT, DIFF)

       最直接的损失函数是平均偏差误差损失，如公式所示。它捕获了预测的平均偏差，但很少被用作损失函数来训练回归模型，因为正误差可能会抵消负误差，从而导致参数的潜在错误估计。然而，它是下一小节定义的损失函数的起点，通常用于评估模型的性能。

       直接连接到 MBE 分别存在平均绝对误差、均方误差和对数cosh损失，这在如何利用偏差方面基本上与 MBE 不同。 

4.0.2平均绝对误差损失(L-CONT,CONV)

       平均绝对误差损失或 L1 损失是回归最基本的损失函数之一，它衡量预测中绝对偏差的平均值。绝对值克服了 MBE 的问题，确保正错误不会抵消负错误。因此，每个误差的贡献与误差的绝对值成比例。请注意，错误的贡献遵循线性行为，这意味着许多小错误作为一个大错误很重要。这意味着梯度幅度不依赖于误差大小，因此当误差较小时可能会导致收敛问题。当以输入为条件的目标数据是对称的时，经过训练以最小化 MAE 的模型更有效。需要强调的是，没有定义绝对值在零的导数。

       至于 MBE，MAE 还用于评估模型的性能

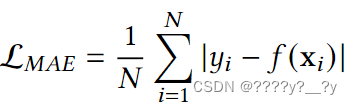
4.0.3均方误差损失(CONT, DIFF, CONV)

       均方误差损失，或 L2 损失，是观测值和预测值之间的平方距离的平均值。至于MAE，它是一个著名的、直接的回归损失函数。平方项使所有偏差都为正，放大了异常值的贡献，使其更适合于观测值中的噪声服从正态分布的问题。主要缺点是对异常值的敏感性。 

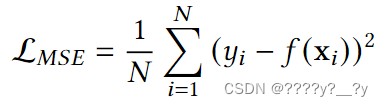
4.0.4均方根误差损失(CONT,DIFF,CONV)

       直接连接到 MSE，我们有均方根误差损失，类似于 MSE，除了平方根项。主要优点是确保损失具有相同的单位和感兴趣的变量的规模。由于 MSE 和 RMSE 之间的唯一差异在于根项的应用，最小化过程收敛到相同的最优值。然而，根据所使用的优化技术，RMSE 可能会采取不同的梯度步骤。与之前提出的损失函数一样，它也被用作比较模型性能的指标，并且具有相同的限制。 

4.0.5 Huber 损失 (L-CONT,DIFF,S-CONV)

       Huber损失是MAE的一种变体，当残差很小时，它就变成了MSE。它由𝛿参数化，它定义了从MAE到MSE的过渡点。当|yi−𝑓(xi)|≤𝛿时，Huber损失服从MSE，否则服从MAE。这使得它结合了MAE和MSE的优点，当预测和模型输出之间的差异很大时，误差是线性的，使得Huber损失对异常值不那么敏感。相反，当误差较小时，它遵循MSE，使得收敛速度快得多，并且在0处可微。𝛿的选择是基本的，它可以在训练过程中根据被认为是异常值的情况不断调整。Huber损失的主要限制在于额外的超参数𝛿。 

请注意，当 𝛿 = 1 时，我们得到平滑的 L1 损失。

4.0.6对数双曲余弦损失(CONT, DIFF) 

       log-cosh损失是观测值与预测值之间的残差的双曲余弦的对数。它具有Huber损失的所有优点，不需要设置超参数，但代价是计算成本更高。此外，log-cosh损失的另一个好处是，它在任何地方都是可微的，这使得它适用于需要求解二阶导数的方法。由于𝑙𝑜𝑔(𝑐𝑜𝑠<e:1> (x))近似等于x22，对于x的小值，它的行为类似于MSE。对于较大的x值，则几乎等于|x|−𝑙𝑜𝑔(2)，使其与MAE相似。

该损失函数的另一个缺点是，与 Huber 损失相比，它不太可定制。

4.0.7均方根误差损失(CONT,DIFF,CONV) 

       均方根对数误差(RMSLE)损失是对数变换后的观测值和对数变换后的预测值的均方根误差(RMSE)。关于RMSE的唯一区别是对数同时应用于预测值和观察值。对数中的+ 1项允许𝑓(x±)的值为零。
       由于对数的性质，预测值与实际值之间的误差是相对的，这使得RMSLE对异常值具有更强的鲁棒性。准确地说，RMLSE的大小与误差的大小没有相应的比例。事实上，当预测值和实际值都很高时，残差较大的数据点受到的惩罚较小。这使得RMSLE适合于目标具有指数关系的问题，或者惩罚低于估计的问题比惩罚高于估计的问题更可取。但是，这种损失不适用于允许负值的问题。

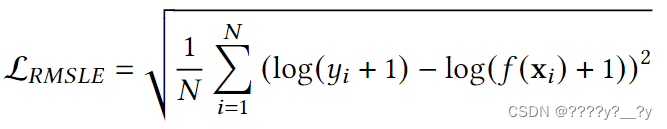
五、分类损失 

5.1问题表述和符号

       分类是属于监督学习问题的一个子集。目标是将输入分配给𝐾离散类之一。这个目标可以通过最小化损失函数𝐿来训练模型𝑓Θ及其参数Θ来实现。设𝑓的目标空间离散，考虑一个返回输出标签的模型，则𝑓可以定义为:

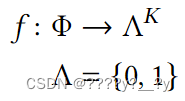
       上述定义也适用于多标签分类，因为一个样本可以关联多个标签，例如𝑓(x) =[0,1,0,1,0,0]。为了定义单标签分类，我们需要添加输出之和为1的约束，
       我们还可以考虑具有连续输出的模型，如果它们为每个可能的可分配标签𝑘∈1，…k，返回概率𝑝𝑘(x)∈[0,1]到样本x:

       和以前一样，要在多标签和单标签分类之间切换，如果我们想强制分配单个标签，我们需要约束概率输出之和为1。
       为了描述二元分类问题，可以引入一种更狭义的分类符号。这种符号在这项工作中很有用，因为基于保证金的损失是为了解决二元分类问题而设计的，不能推广到多类或多标签分类。对于二元分类问题的子集，𝑓的目标空间是离散的，其定义如下: 

       根据所采用的优化策略，我们定义了两种不同的分类损失宏观类别，即基于边际的和概率的，如图3所示。在下一节中，我们将介绍基于保证金的损失函数，从最基本和直观的0 - 1损失开始。随后，我们提出了铰链损失及其变体(平滑和二次平滑铰链损失)。然后，描述了修正Huber损失、Ramp损失和余弦相似度损失。此外，我们通过引入交叉熵损失和负对数似然损失来引入概率损失，从数学的角度来看，它们是一致的。最后给出了Kullback-Leibler散度损失。 

5.2基于边际的损失函数

       在本节中，我们将介绍最著名的基于边际的损失函数。 

5.2.1零一损失

       基于基本更直观的基于边际的分类损失是零一损失。它将 1 分配给错误分类的观察，将 0 分配给正确分类的观察。

       零损失不能直接使用，因为它缺乏凸性和可微性。然而，有可能得出经过分类校准的可雇用的替代损失，这意味着它们是𝐿𝑍𝑒𝑟𝑜𝑂𝑛𝑒的松弛，或上界，或这种损失的近似值。最近关于二元分类的文献的一个重要成就是确定了这些松弛产生费雪一致性的充分必要条件。以下所有损失都满足这些条件。

5.2.2 铰链损失和感知器损失 (L-CONT,CONV)

       最著名的替代损失是Hinge损失，它对结果一致性<= 1的每个预测都进行线性惩罚。

       Hinge损失不是严格凸的，但它是Lipschitz连续和凸的，所以机器学习中使用的许多通常凸优化器都可以与之一起工作。铰链损失通常用于优化支持向量机

       为了训练感知器使用了这种损失的变体，即感知器损失。这种损失与 Hinge 损失略有不同，因为它不会惩罚边缘内的样本，围绕分离超平面，而只是用具有相同线性惩罚的超平面错误标记的样本。

        使用铰链损失有两个主要缺点。首先，它采用使模型对训练数据中的异常值敏感。其次，由于导数 𝑓 (x) · 𝑦) = 1 的不连续性，即不连续可微的事实，铰链损失结果难以优化。

5.2.3 平滑铰链损失 (L-CONT,CONV)

        定义了 Hinge 损失的平滑版本，目的是获得更容易优化的函数，如下所示：

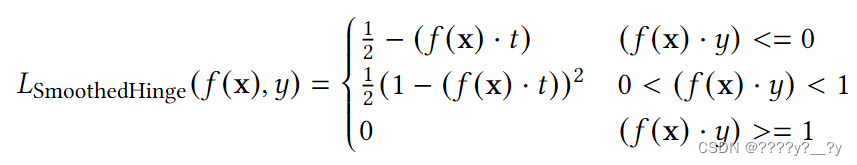
        这个平滑版的Hinge损失是可微的。显然，这不是铰链损失的唯一可能的平滑版本。然而，它是一个典型的函数，它有一个重要的性质，即在 z>= 1时为零，并且在 z≤0 时斜率为常数(负)。而且，当斜率为 0<z<1 时，损失平滑地从斜率为0过渡到常数为- 1。这种损失继承了原始Hinge损失对异常值的敏感性。 

5.2.4二次平滑铰链损失 (L-CONT,CONV,DIFF)

        出于平滑 Hinge 损失的相同目标，在中定义二次平滑版本，使其更容易优化：

超参数 𝛾 确定平滑程度，对于 𝛾 → 0，损失变为原始铰链。与平滑铰链损失相比，该版本在整个域中是不可微的。 

5.2.5 修改后的 Huber 损失 (L-CONT, DIFF, S-CONV)

        修改后的 Huber 损失是回归的 Huber 损失的轻微变化，以及 𝛾 = 2 的二次平滑 Hinge 损失的特例（更多详细信息请参阅第 4.0.5 节）：

5.2.6 Ramp 损失 (CONT,CONV)

       Ramp 损失或截断 Hinge 是中提出的分段线性、连续和凸损失。在多类设置下，这种损失对异常值更稳健。在 SVM 中使用时，它使用更小、更稳定、更稳定的支持向量集生成更准确的分类器，而不是使用 ShakeHinge 的多类 SVM，并且还保留了 fisher 一致性。 

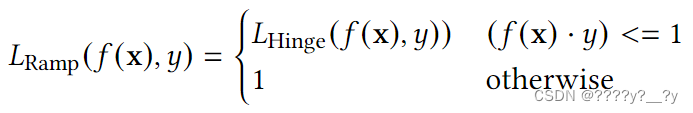
5.2.7 余弦相似度损失 (L-CONT,DIFF)

       余弦相似度通常用作度量距离的度量，当矢量的大小不重要时。一个典型的例子是通过单词计数来表示文本数据。当标签和输出可以解释为向量时，可以推导出它们之间的距离度量，该度量可以改编为损失函数，如下所示:

       重要的是要强调，当使用余弦相似性损失时，可能值的范围被限制在区间[- 1,1]，这可能不适合所有类型的数据或应用程序，特别是当可解释性是一个关键要求时。

5.3概率损失函数

       设𝑞为数据集底层的概率分布，𝑓Θ为生成输出的函数，概率损失函数提供𝑞和𝑓Θ之间的距离函数。通过最小化该距离，模型输出分布收敛于地面真值1。通常，用概率损失函数训练的模型可以提供一个样本被标记为一个类的可能性，而不是另一个类，提供更丰富的基于边际的信息。

5.3.1交叉熵损失和负对数似然损失(CONT,DIFF,CONV)

       最大似然估计 (MLE) 是一种通过最大化似然来估计概率分布参数的方法。从贝叶斯推理的角度来看，MLE 可以被认为是最大后验估计 (MAP) 的一种特殊情况，它假设参数的均匀分布。形式上，这意味着，给定一个样本 D 的数据集，我们最大化以下数量：

       目的是通过最小化损失函数来找到最大似然估计。为了最大化等式，我们可以通过使用负对数似然将其转换为最小化问题。为了实现这个目标，我们需要定义以下数量：

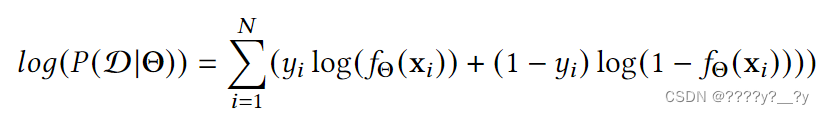
       我们可以通过取对数的负来获得损失函数：

       通常，上述损失也称为交叉熵损失，因为它可以通过最小化 fΘ 和 q 之间的交叉熵来导。

       对于离散情况（这是我们感兴趣的情况）交叉熵的定义是：

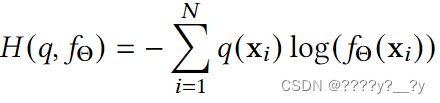
       最大化关于参数 Θ 的可能性与最小化交叉熵相同，如以下等式所示：

       将这种损失扩展到多类场景的经典方法是在模型的最后激活时添加一个softmax函数，该函数根据所考虑的(𝐾)类的数量进行定义。给定每个类的分数𝑓𝑘(x) =𝑠，它的输出可以通过softmax函数𝑓𝑆压缩为1，得到:

其中，softmax 定义如下：

最终损失（通常称为分类交叉熵）是：

5.3.2 Kullback-Leibler 散度 (CONT, CONV, DIFF)

       Kullback-Leibler (KL)散度是一种基于信息的概率分布差异度量。准确地说，它是对一个概率分布与另一个概率分布差异的非对称测量。从技术上讲，KL散度不是距离度量，因为它不服从三角不等式(𝐾𝐿(𝑞||𝑓Θ)不等于𝐾𝐿(𝑓Θ||𝑞))。重要的是要注意，在分类用例中，最小化KL散度与最小化交叉熵是相同的。精确地说，两个连续分布之间的KL定义为:

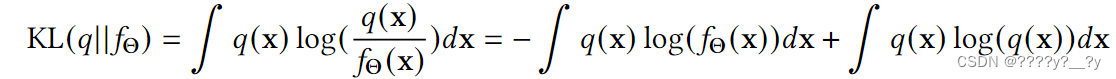
如果我们想最小化参数Θ上的KL，因为第二个积分不依赖于Θ，我们得到:

       一般来说，最好使用交叉熵，而不是KL散度，因为它通常更容易计算和优化。交叉熵只涉及对数据的单个和，而KL散度涉及双和。这可以提高计算效率，特别是在处理大型数据集时。

六、生成损失

       近年来，生成模型在理解数据分布的复杂性和能够重新生成数据方面变得特别有用。在本节中，如图4所示，我们描述了与生成对抗网络(gan)和扩散模型相关的损失。然而，生成模型并不局限于这些情况，而是扩展到包括更多的模型。例如，变分自编码器(VAEs)，其中kl -散度是所使用的损失函数，如第5.3.2节所述。VAE损失的目标是减小原始分布与预测分布之间的差异。其他模型如像素递归神经网络和实值非体积保留(realNVP)模型在本调查中没有考虑。

6.1生成对抗网络

       生成对抗网络(GANs)用于从训练数据中采样创建新的数据实例。gan有两个主要组成部分:
       •生成器，称为𝐺({z0，···，z𝑁})，它从随机噪声中生成数据，并试图复制真实的数据分布

       •鉴别器，称为𝐷({x0，···，x𝑁})，它学习区分生成器的假数据和真数据。对产生与真实数据相区别的假数据的发生器损失进行处罚。
       GAN架构相对简单，尽管有一个方面仍然具有挑战性:GAN损失函数。准确地说，鉴别器被训练为生成器提供损失函数。如果生成器训练顺利，鉴别器在区分真实样本和假样本方面会变得更差。它开始将虚假数据分类为真实数据，其准确性下降。
       发生器和鉴别器组件都是典型的神经网络，其中发生器输出直接连接到鉴别器输入。鉴别器的分类提供了一个信号，生成器使用该信号通过反向传播更新其权重。
       当GAN试图复制概率分布时，它们应该使用损失函数来反映GAN生成的数据分布与真实数据分布之间的距离。
       两种常见的氮化镓损失函数通常使用:极小最大损失和瓦瑟斯坦损失。产生器和鉴别器损失来源于上述两个概率分布之间的单个距离度量。生成器只能影响距离度量中的一个项:反映假数据分布的项。在生成器训练过程中，我们去掉另一项，它反映了真实的数据分布。产生器和鉴别器的损失看起来不同，尽管它们来自同一个公式。
       在下面，极大极小损失和沃瑟斯坦损失都以一般形式表示。损失函数(CONT, DIFF等)的性质是根据为生成器或鉴别器选择的函数来确定的。

6.1.1 Minimax损失

       生成模型𝐺学习数据分布，并与判别模型𝐷同时训练。后者估计给定样本与训练数据相同的概率，而不是𝐺。𝐺被训练来最大化欺骗𝐷的可能性。换句话说，生成器试图最小化以下函数，而鉴别器试图最大化它:

其中:

•𝐷({x0，···，x𝑁})是鉴别器对真实数据实例{x0，···，x𝑁}为真实的概率的估计，

•𝐸{x0，···，x𝑁}为所有真实数据实例的期望值，

•𝐺({z0，···，z𝑁})为给定噪声{z0，···，z𝑁}时发生器的输出，

•𝐷(𝐺(𝑧))是鉴别器对假实例为真概率的估计，

•𝐸{z0，···，z𝑁}是对生成器所有随机输入的期望值(实际上，是对所有生成的假实例的期望值𝐺({z0，···，z𝑁}))。

       上面的损失函数直接表示了真实数据分布和生成数据分布之间的交叉熵。生成器不能直接影响函数中的log(𝐷({x0，···，x𝑁}))项，它只最小化log(1−𝐷(𝐺({z0，···，z𝑁})))项。这种损失函数公式的一个缺点是，当鉴别器接收到琐碎的任务时，上面的极大极小损失函数可能会导致GAN在训练的早期阶段陷入困境。因此，对损失的一个建议修改是允许生成器最大化log(𝐷(𝐺({z0，···，z𝑁})))。

6.1.2Wasserstein 损失

       Wasserstein距离提供了一种训练生成器的替代方法，以更好地近似训练数据集的分布。在这种设置中，生成器本身的训练负责最小化训练数据集和生成数据集分布之间的距离。可能的解决方案是使用分布距离度量，如Kullback-Leibler (KL)散度、Jensen-Shannon (JS)散度和Earth-Mover (EM)距离(也称为Wasserstein距离)。使用Wasserstein距离的主要优点是它的可微性和连续线性梯度。
       使用Wasserstein损失的GAN(称为WGAN)不像其他GAN那样区分真实分布和生成分布。相反，WGAN鉴别器被称为“批评家”，它对每个实例进行实值评分，而不是预测它是假的概率。这个分数的计算是为了使真实数据和虚假数据之间的距离最大化。
WGAN的优点是训练过程更稳定，对模型结构和超参数的选择不太敏感。
这两个损失函数可以写成:

       鉴别器试图最大化L𝑐𝑟𝑖𝑡𝑖𝑐。换句话说，它试图最大化其在真实实例上的输出与在假实例上的输出之间的差异。发电机试图最大化L𝐺𝑒𝑛𝑒𝑟𝑎𝑡𝑜𝑟。换句话说，它试图最大化鉴别器对其假实例的输出。
       Wasserstein损失的好处是，它提供了一个有用的梯度几乎无处不在，允许模型的持续训练。这也意味着较低的Wasserstein损耗与较好的生成器图像质量相关，这意味着它明确地寻求最小化生成器损耗。最后，它比基于极小值的gan更不容易陷入局部最小值。然而，使用批准确估计Wasserstein距离需要难以承受的批大小，这大大增加了所需的数据量。

6.2扩散模型

       扩散模型是依赖概率似然估计来生成数据样本的生成模型。他们最初是受到一种叫做扩散的物理现象的启发。扩散建模是一种学习过程，在该过程中，模型可以通过迭代地加入轻微的噪声因子来学习信息的系统衰减。学习过程使从噪声中恢复衰减信息成为可能。他们在马尔可夫链中建立了一系列噪声分布模型，并通过系统地分层去除噪声来解码原始数据。
扩散过程包括两个步骤，即正向过程和重构(反向)过程。在前向扩散过程中逐渐加入高斯噪声，直到数据样本失去可区分的特征。反向过程利用神经网络模型学习条件概率密度，去除噪声，恢复原始数据。

6.2.1正向扩散过程

       给定从真实数据分布𝑞(x)中采样的数据点x0。前向过程旨在迭代𝑇次添加小噪声。对于每个数据点x0，该过程产生一系列带噪声的样本x1，···，xT。噪声分布通常选择为高斯分布。由于𝑡时刻的概率密度预测只依赖于𝑡−1时刻的前一时刻，因此条件概率密度可计算为:

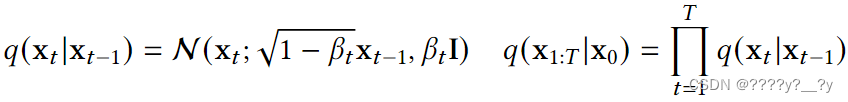
       其中，𝑡∈(0,1)是一个可以作为常量或变量的超参数，𝑡∈[1，𝑇]。当𝑇→∞时，xT成为纯高斯分布。根据随机梯度朗之万动力学，我们只能利用马尔可夫链更新中密度函数的梯度对系统的新状态进行采样。然后可以使用下面的公式来计算时间𝑡的新数据点的采样，步长𝛿取决于时间𝑡−1的前一个点:

       当𝑇→∞时，𝝐→0等于真实概率密度𝑝(x)。向前的一步不需要训练神经网络;它只需要在原始数据分布中加入随机高斯噪声的迭代过程。

6.2.2反向扩散过程

       给定系统的当前状态，反向过程需要计算前一个时间步长的概率密度。在𝑡=𝑇时计算𝑞(x𝑡−1|x𝑡)等于从各向同性高斯噪声中产生数据。然而，与正演过程相反，从当前状态估计过去状态需要知道之前的每个梯度，如果没有可以预测这种估计的学习模型的帮助，这是不可行的。这个问题是通过训练一个神经网络模型来解决的，该模型使用学习到的权重Θ和当前状态𝑡，估计𝑝Θ(x𝑡−1|x𝑡)的值，如以下公式所示:

其中𝝁Θ(x𝑡，𝑡)为中提出的均值函数。此时𝑡−1时刻的样本可以计算为:

6.2.3扩散模型损失函数(CONT, DIFF)

       网络模型的主要任务是最小化以下损失：

       结果表明，简化后的𝐿diffusion可以获得更好的结果:

       值得注意的是，尽管扩散模型在计算上比其他深度网络结构更昂贵，但在某些应用中表现得更好。

七、排名损失

       机器学习可以用来解决排名问题，这在工业上有重要的应用，特别是在信息检索系统中。这些问题通常可以通过使用监督学习、半监督学习或强化学习来解决。
与其他损失函数(如交叉熵损失或MSE损失)相比，排序损失的目标是预测输入之间的相对距离，而不是学习预测给定输入的标签、值或一组值。这有时也被称为度量学习。然而，交叉熵损失可以用于前一概率排序。在此场景中，给定所有对象的分数，该模型中对象的前一概率表示该对象将排名第一的可能性。
       训练数据的排序损失函数是高度可定制的，因为它们只需要一种方法来衡量两个数据点之间的相似性，即相似性得分。例如，考虑一个人脸验证数据集，属于同一个人的照片对将具有高相似性得分，而不属于同一个人的照片对将具有低相似性得分。
       一般来说，排序损失函数需要对两个(或三个)数据实例进行特征提取，然后为每个实例返回嵌入的表示。然后可以定义度量函数来度量这些表示之间的相似性，例如欧几里得距离。最后，对特征提取器进行训练，以便在输入是相似的情况下为两个输入产生相似的表示，或者在不相似的情况下为两个输入产生遥远的表示。
       与第6节类似，双序和三重序排序损失以一般形式呈现，如图5所示。损失函数(CONT, DIFF等)的性质是根据所选择的度量函数来确定的。

7.1 成对排名损失

       在成对排序损失的情况下，使用训练数据点的正对和负对。正对由锚样x𝑎和正样x𝑝组成，正样x𝑝与度规中的x𝑎相似。负对由锚样本x𝑎和负样本x𝑛组成，这与该度量中的x𝑎不同。目标是学习它们之间的距离较小𝑑的表示，对于正对和大于一些边际值𝑚的表示，对于负对。成对排序损失迫使表示对于正对具有0距离，对于负对具有大于余量的距离。
给定输入样本x𝑎，x𝑝，x𝑛和𝑑的嵌入表示(特征提取器的输出)r𝑎，r𝑝和r𝑛作为距离函数，损失函数可以写成:

       对于正对，如果对中两个元素的嵌入表示之间的距离为0，则损失将消失;相反，损失将随着两个表示之间距离的增加而增加。对于负对，如果两个元素的嵌入表示之间的距离大于边际𝑚，则损失将消失。但是，如果距离小于𝑚，则损失将为正，并且模型参数将被更新，以提供距离较远的两个项目的表示。当r𝑎与r𝑛之间的距离为0时，损失值最多为𝑚。余量的目的是为足够远的负对创建表示，从而隐含地停止对这些对的训练，并允许模型专注于更具挑战性的对。如果r0和r1是对元素的表示形式，那么对于负对和正对，其值分别为0和1，其中的距离𝑑为欧氏距离:

       与典型的分类学习不同，这种损失需要更多的训练数据和时间，因为它需要在训练期间访问所有潜在对的所有数据。此外，由于训练涉及到成对学习，它将输出与每个类的二进制距离，如果存在不正确的分类，则计算成本更高。

7.2 Triplet排名损失

       使用三元组而不是成对的训练数据实例可以产生更好的性能。由此产生的损失称为三重排序损失。三联体由锚样x𝑎、阳性样x𝑝和阴性样x𝑛组成。目标是锚点样本和负样本表示之间的距离𝑑(r𝑎，r𝑛)比锚点样本和正样本表示之间的距离𝑑(r𝑎，r𝑝)更大(并且大于一个边际𝑚)。同样的符号也适用:

       根据r𝑎、r𝑝、r𝑛和𝑚的值，该损失有三种不同的情景特征:
•容易三胞胎:𝑑(r𝑎,r𝑛)>𝑑(r𝑎,r𝑝)+𝑚。在嵌入空间中，负样本与锚样之间的距离已经足够大。模型参数不变，损失为0。
•硬三胞胎:𝑑(r𝑎，r𝑛)<𝑑(r𝑎，r𝑝)。与正样本相比，负样本更靠近锚点。损失是正的(>𝑚)。模型的参数可能会改变。
•半硬质三胞胎:𝑑(r𝑎,r𝑝)<𝑑(r𝑎,r𝑛)<𝑑(r𝑎,r𝑝)+𝑚。损失仍然是正的(和<𝑚)，然而，负样本比正样本离锚点更远。模型参数会发生变化，损失不为0。
       这种损失对输入样本的微小变化很敏感，因此不能推广。这意味着，一旦模型在特定数据集上进行了训练，它就不能应用于其他数据集。

八、基于能量的损失

       基于能量的模型(EBM)是一种概率模型，它使用标量能量函数来描述模型变量的依赖关系。EBM可以形式化为:X × Y→R，其中的变量(X, Y)表示(X, Y)对之间的关系。
给定一个能量函数和输入x，计算y的最佳拟合值，推理过程如下:

       基于能量的模型提供了完全生成的模型，可以用作预测、分类或决策任务的概率估计的替代方案。
当且仅当集合y的大小足够小时，对于y∈y = {y0，···，y𝑁}的所有值，可以显式定义能量函数𝐸(x, y)≡𝐹(x, y)。相反，当Y的空间足够大时，必须采用一种称为推理过程的特定策略来找到最小化𝐸(x， {y0，···，Y𝑁})的Y。

       在许多真实的情况下，推理过程可以产生一个近似的结果，这个结果可能是，也可能不是给定x的𝐸(x， {y0，···，y𝑁})的全局最小值。此外，可能𝐸(x， {y0，···，y𝑁})有几个等价的最小值。使用的最佳推理程序通常取决于模型的内部结构。例如，如果Y是连续的，并且𝐸(x， {y0，···，Y𝑁})关于Y的处处光滑可微，则可以采用基于梯度的优化算法。

一般来说，对于x∈R𝐷，任意概率密度函数𝑝(x)都可以重写为EBM:

其中，能量函数()可以是任意函数(Θ)参数化(如神经网络)。在这些模型中，通过固定条件变量的值来进行预测(例如找到𝑝(x0|x1, x2，…))，并通过最小化能量函数来估计剩余变量(例如x0)。

     通过找到一个能量函数来训练EBM，该函数将低能量与从基础数据分布中提取的x值联系起来，𝑝𝜃(x) ~𝑝𝐷(x)，以及不接近基础分布的x值的高能量联系起来。

8.1训练

      在上述概念框架下，训练可以被认为是在每一步中找到定义输出(y∈y)和输入(x∈x)之间良好匹配的模型参数。这是通过扫描所有模型参数Θ从能量函数集(E)中估计最佳能量函数来完成的，其中E ={𝐹(Θ， X, Y): Θ∈W = Θ}。损失函数的行为应该与公式47中描述的能量函数相似，即正确答案的较低能量必须由低损失来建模，而所有错误答案的较高能量则由较高损失来建模。
考虑一组训练样本S = {(x𝑖y𝑖):𝑖= 1 , · · · , 𝑁},在培训过程中,损失函数的影响应该压低𝐸(Θy𝑖x𝑖)和把𝐸(Θ˜y𝑖x𝑖),即找到将损失最小化的参数Θ:

损失函数L𝑒𝑏𝑚的一般形式定义为:

其中:
•𝐿𝑒𝑏𝑚(y𝑖，𝐸(Θ， y, x𝑖))是每个样本的损失

y𝑖是期望的输出

•𝐸(Θ， Y, x𝑖))是给定x𝑖在Y∈Y变化时的能面

      这是训练集上每个样本损失函数的平均值，表示为𝐿𝑒𝑏𝑚(y𝑖，𝐸(Θ， y, x𝑖))。该函数依赖于期望的输出y满满，依赖于保持输入样本x满满不变，改变对样本y的输出扫描所得到的能量。根据此定义，当训练样本混合或训练集重复多次时，损失保持不变。随着训练集的增长，模型过拟合的可能性越来越小。

8.2EBM的损失函数

      在图6之后，在本节中，我们首先介绍能量损失，因为它是最直接的。然后，我们介绍了机器学习中常见的损失，这些损失可以适应基于能量的模型，例如负对数似然损失、Hinge损失和Log损失。随后，我们引入了更复杂的损失，如广义感知器损失和广义边际损失。最后给出了最小分类误差损失、平方损失及其方差平方指数损失。

8.2.1 能量损失

      由于其简单性，所谓的能量损失是最直接的损失。它可以简单地用能量函数作为每样本损失来定义:

      这种损失通常用于回归任务。根据其定义，它将能量函数向下拉取接近正确数据分布的值。然而，能量函数不会因为不正确的值而被拉上来。假设是，通过降低正确位置的能量函数，不正确值的能量会更高。由于这种假设，训练对模型设计很敏感，可能导致能量崩溃，导致能量函数很大程度上是平坦的。

8.2.2 广义感知器损失 (L-CONT, CONV)

      广义感知器损失定义为：

      这个损失是正定的，因为第二项是第一项的下界。，𝐸(Θ， y𝑖，x𝑖)−[𝑚𝑖𝑛y∈y]{𝐸(Θ， {y0，···，y𝑁}，x𝑖)}≥0。通过最小化此损失，下推第一项并提高模型预测的能量。虽然它被广泛使用，但这种损失是次优的，因为它没有检测到正确输出和错误输出之间的差距，并且它不限制函数为每个错误输出分配相同的值，并且它可能产生平坦的能量分布。

8.2.3 负对数似然损失 (CONT,DIFF,CONV)

      与第5.3.1节的描述类似，基于能量的上下文中的负对数似然损失(NLL)定义为:

其中S为训练集。

      这种损失减少为感知机损失，当时延为0→∞时，这种损失减少为Y只有两个标签(即二值分类)时的对数损失。由于上述积分是难以处理的，因此已经花费了大量的精力来寻找近似方法，包括蒙特卡罗采样方法和变分方法。虽然这些方法被设计为最小化NLL损失的近似方法，但在基于能量的框架中，它们可以被视为选择能量将被拉上来的y的不同策略。NLL也被称为交叉熵损失，广泛应用于许多应用，包括基于能量的模型。这种损失函数公式也受到5.3.1节中列出的限制。

8.2.4 广义边际损失

      广义边际损失是广义感知器损失的一种更可靠的形式。能量训练中广义边际损失的一般形式定义为:

      ¯y𝑖是所谓的“最不正确输出”,这是最低能量的输出在所有可能的输出不正确的[64],𝑚是一个积极的边缘参数,𝑄𝑚凸函数,确保接收低损失值𝐸(𝑖Θ,x, y𝑖)和高值𝐸(Θ、x𝑖¯y𝑖)。换句话说，损失函数可以确保最令人讨厌的错误输出的能量比正确输出的能量大任意余量。

      这个损失函数是用一般形式写的，各种各样的损失使用特定的边际函数𝑄𝑚来产生正确输出和错误输出之间的差距，这些损失在本节的以下部分被形式化。

1、Hinge loss (L-CONT,CONV)

      可以在 5.2.2 节中解释，铰链损失可以重写为：

      这种损失强制要求正确答案和最令人反感的错误答案之间的差异至少为𝑚。单个能量不需要取一个特定的值，因为铰链损失取决于能量差。该损失函数与原始Hinge损失具有相同的局限性。

2、Log loss (DIFF,CONT,CONV)

      这种损失类似于hinge损失，但它在正确输出和最冒犯的输出之间设置了更软的间隔。日志损失被定义为:

      这种损失也被称为软铰链，它可能会在高维数据集上产生过拟合。

3、最小分类错误损失(CONT, DIFF, CONV)

      一个简单的函数，粗略地计算分类错误的总数，同时保持光滑和可微，被称为最小分类错误(MCE)损失。MCE被写成一个sigmoid函数:

      虽然这个函数没有明确的边界，但它仍然会在最令人讨厌的错误输出和正确输出之间产生能量差。

4、Square-square loss (CONT,CONV)

      Square-square损失处理正确输出的能量𝐸(Θ， x𝑖，y𝑖)和最进攻性输出的能量𝐸(Θ， x𝑖，¯y𝑖)不同:

      这种组合旨在将正确输出的能量最小化，同时对最令人反感的错误输出强制执行至少𝑚的余量。这个损失是保证金损失的修改版本。只有当能量函数有一个下界时，才能使用这种损失。

5、平方指数损失(CONT, DIFF, CONV)

这个损失函数类似于square-square损失函数，只是第二项不同:

      虽然𝛾是一个正常数，但这一组合的目的是将正确输出的能量最小化，同时将最令人讨厌的错误输出的能量推向无限边缘。这种损失被认为是前面提到的平方损失的正则化版本。与Square-square损失一样，这种损失只能在能量函数存在下界时使用。

九、总结

      适当的损失函数的定义是解决许多机器学习问题的关键部分。在本调查中，我们从机器学习文献中描述了33个最常用的损失函数。这些函数适用于解决广泛的问题，包括分类、回归、样本生成和排序。总的来说，我们努力为机器学习文献的新手和高级从业者提供有用的资源。
我们描述的每一个损失函数也都被放到了上下文中，并在第2节中介绍的一种新的分类中进行了比较。这为从业者提供了不同技术的快速视图以及它们如何组合在一起，允许他们快速有效地决定和选择最适合他们技术的方法。我们也希望这个框架可以帮助研究人员将新开发的损失函数置于背景中。