量子隐形传态

        原理：量子隐形传态（Quantum Teleportation）是一种量子信息传输的过程，它利用了量子纠缠的特性，而不是传统的经典信息传输方法。在量子隐形传态中，量子态（通常是一个粒子的状态，如电子或光子）被传输到空间中的另一个位置，而且这个传输过程并不涉及粒子本身穿越空间的移动。

量子电路图：

Alice要给Bob传递信息q0，则在Alice和Bob之间创造一个纠缠态，即利用q1和q2创造纠缠态。 

一、量子纠缠创建

        纠缠态是量子力学中一个重要而奇特的概念。在量子力学中，粒子的状态不能被完全确定，而是通过波函数描述。纠缠态涉及多个粒子，当它们之间发生相互作用后，它们的状态就会被紧密关联，即使它们之间的距离很远。

        具体而言，如果两个或更多粒子被纠缠在一起，它们的状态就无法被单独描述，而只能通过整体系统的波函数来描述。这就导致了一种奇特的关系：当我们测量一个粒子的状态时，它会立即影响到与之纠缠的其他粒子，即使它们之间的距离很远，似乎瞬间就发生了信息的传递。

1、贝尔态（Bell state）

贝尔态是一种特殊的纠缠态，描述了两个粒子之间的关联。一共有四种情况：

2、创建贝尔态

这里创建的是：

二、初始化量子态

总共涉及三个量子，初始化三个量子的量子态，即求解bell态与q0的张量积：
设q0的量子态为：

初始化三个量子的量子态：

三、CNOT门和H门

1、q0与q1构建CNOT门，即q0为1的时候q1取反，q0为0的时候则不进行操作，故CNOT之后的结果为：

2、q0经过H门，H门为创造纠缠量子态，量子0变为+态，量子1变为-态，具体如下：

故对q0进行操作，结果如下：

四、测量

测量的时候是测量q0和q1，故将结果q0、q1放在一起：

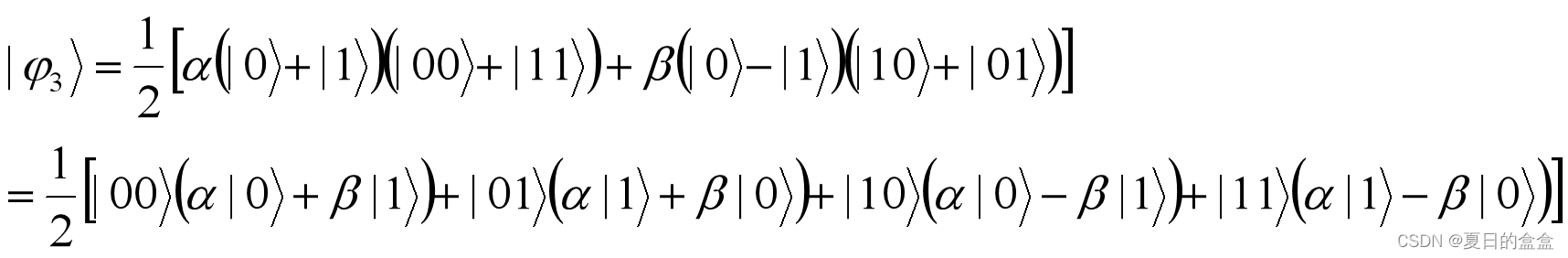
 画线的地方为q2的位置，故存在四种情况：

1. 如果测量结果是“00”，那么Bob手上的量子比特就是 |ψ〉；
2. 如果测量结果是“01”，那么Bob对他手上的量子比特作用 X 门就得到了 |ψ〉；
3. 如果测量结果是“10”，那么Bob需要作用 Z 门；
4. 如果测量结果是“11”，那么Bob需要先作用 X 门，再作用 Z 门。

五、信息传递 

        Alice将q0和q1的测量结果同经典电路发送给Bob，Bob通过测量的结果进行相应的变换来获得要传输的q0。整个过程里面并未传递q0的任何信息，因为通过了经典电路发送信息，故整个过程不超过光速。

六、代码及结果

1、代码，基于华为云平台MindSpore

from mindquantum.core.circuit import Circuit
from mindquantum.core.gates import H, CNOT, Measure, X, Z, BARRIER
from mindquantum.simulator import Simulator
from IPython.display import display_svg
import numpy as np

psi = np.random.rand(2)
psi = psi / np.linalg.norm(psi)
print(f"psi = {psi}")
bell = np.array([1, 0, 0, 1]) / np.sqrt(2)

init = np.kron(bell,psi)


sim = Simulator("mqvector", 3)
sim.set_qs(init)

circ = Circuit()
circ += CNOT.on(1, 0)
circ += H.on(0)
circ += BARRIER
circ += Measure("q0").on(0)
circ += Measure("q1").on(1)

#采样一百次
#res = sim.sampling(circuit=circ, shots=100)
#print(res)

res = sim.apply_circuit(circ)
print(res)

print(sim.get_qs(True))

# if measurement of q1 is 1, then apply X
if res.samples[0][res.keys_map['q1']] == 1:
    sim.apply_gate(X.on(2))
# if measurement of q2 is 1, then apply Z
if res.samples[0][res.keys_map['q0']] == 1:
    sim.apply_gate(Z.on(2))

print(circ)
print(sim.get_qs(True))

2、结果分析

第一行为q0的初始态，倒数一二行为最后的输出结果，三个量子的顺序为q2q1q0，倒数三四行为测量后的结果。

（1）q0初始态：α=0.82094829，β=0.57100254

         测量之后的叠加态：α=0.57100254 ，β=0.82094829
         测量结果为01，需要对Bob的量子比特进行X门操作从而得到q0

（2）q0初始态：α=0.99829708，β=0.05833466

         测量之后的结果为：α=0.99829707，β=0.05833466 
         测量结果为00，需要对Bob的量子比特不进行操作从而得到q0

（3）q0初始态：α=0.9252867，β=0.37926841

         测量之后的叠加态为：α=-0.37926841，β=0.9252867
         测量结果为11，需要对Bob的量子比特进行X门操作后在进行Z门操作从而得到q0

（4）q0初始态：α=0.35527569，β=0.93476157

         测量之后的叠加态为：α=0.35527569，β=-0.93476157
         测量结果为10，需要对Bob的量子比特进行Z门操作从而得到q0