两个重要极限
第一个重要极限公式是:lim((sinx)/x)=1(x->0)
第二个重要极限公式是:lim(1+(1/x))^x=e(x→∞)

间断点的判断

渐近线


反函数

泰勒中值定理和常见的麦克劳林公式


曲线绕x轴体积和表面积公式

体积
1、绕x轴旋转时,微体积 dV = πy^2dx,或者:dV = π(sinx)^2dx,将dV在0到π之间对x做定积分。
得到:V = ∫π(sinx)^2dx (在0到π区间积分) = ∫π(1-cos2x)/2dx (在0到π区间积分) = 0.5π^2。即,给定函数,绕x轴旋转得到的旋转体体积为 0.5π^2。
2、绕y轴旋转时,微体积 dV = π(2x)ydx,或者:dV = 2πxsinxdx,将dV在0到π之间对x做定积分。
得到:V = ∫ 2πxsinxdx(在0到π区间积分) =2π ∫xsinxdx (在0到π区间积分) = 2π^2。即,给定函数,绕y轴旋转得到的旋转体体积为 2π^2。
表面积
S= ∫πy√1+y’^2dx
曲率及曲率半径

曲率半径等于曲率倒数
切线方式和法线方程
切线方程y-y0=f’(x0)(x-x0)

常见的凑微原函数
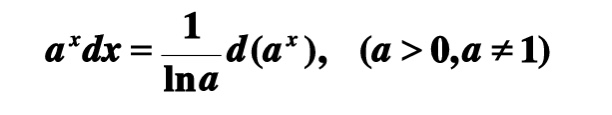


积分变现问题在0到x区间内积分g(x-t)dt 等于0到x区间内积g(u)du
积分定义求极限 i从1到n的问题
先提出1/n i/n化成x 0到1 对其进行积分


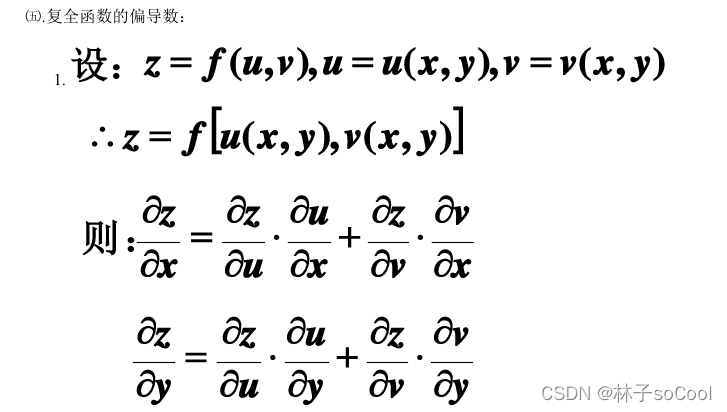



常见函数图像






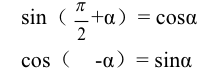
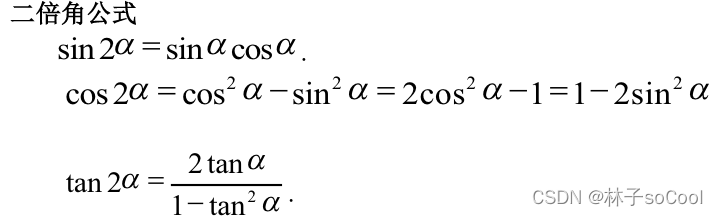



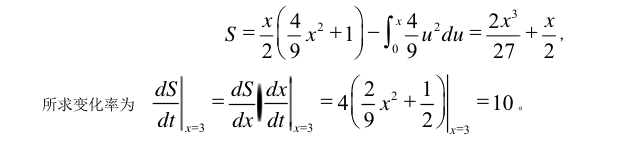
一阶线性微分方程组

二阶线性微分方程





线性代数


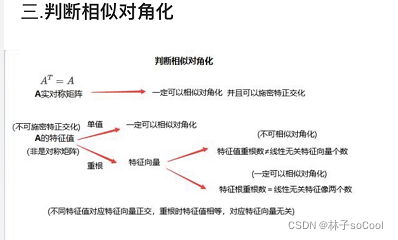




判断向量能否由向量组线性表示,先求A的质在求增广矩阵的质相当就可以表示,不相等不可以表示。






























 这篇博客探讨了数学在信息技术领域的关键应用,包括重要极限公式、间断点的判断、泰勒中值定理、积分计算、曲线旋转体积与表面积的求解、曲率和切线方程。还涉及了一阶和二阶线性微分方程以及线性代数中的向量表示问题。
这篇博客探讨了数学在信息技术领域的关键应用,包括重要极限公式、间断点的判断、泰勒中值定理、积分计算、曲线旋转体积与表面积的求解、曲率和切线方程。还涉及了一阶和二阶线性微分方程以及线性代数中的向量表示问题。
















 8万+
8万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








