线性代数——个人理解

最新推荐文章于 2025-03-03 00:33:06 发布

小小老大MUTA️

最新推荐文章于 2025-03-03 00:33:06 发布

阅读量1.9k

点赞数 8

分类专栏：线性代数文章标签：线性代数

本文链接：https://blog.csdn.net/qq_50645064/article/details/126784943

版权

线性代数专栏收录该内容

6 篇文章

订阅专栏

麻省理工学院 - MIT - 线性代数（我愿称之为线性代数教程天花板）_哔哩哔哩_bilibili

MIT—线性代数笔记00 - 知乎 (zhihu.com)

一、线性方程组的几何图像

二元情况

$2x-y=0$

$-x+2y=3$

Ax=b

该方程可以理解为两种图像：行图像和列图像

行图像

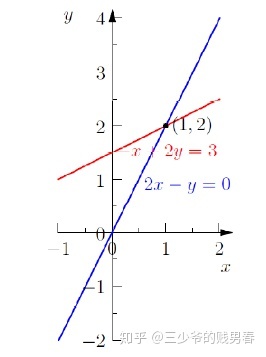
先找出符合方程的两个数组，确定xy平面上两点，连接两点确定代表方程的直线，两条直线的交点为方程组的解；

列图像

先将系数矩阵写成列向量的形式，求解原方程变成寻找列向量的线性组合构成向量b

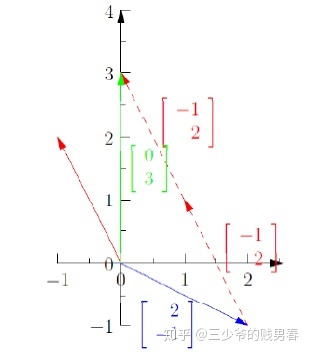
$x\begin{bmatrix} 2\\-1 \end{bmatrix}+y\begin{bmatrix} -1\\2 \end{bmatrix}=\begin{bmatrix} 0\\ 3 \end{bmatrix}$

由图可的x=1，y=2

任意取x,y，以上两个列向量的所有线性组合可以布满整个坐标平面

三元情况

Ax=b方程组是否有解？

行图像理解

当方程所代表的三个平面相交于一点时方程有唯一解；三个平面中至少两个平行则方程无解；平面的两两交线互相平行方程也无解；三个平面交于一条直线则方程有无穷多解。

列图像理解

列向量的线性组合是否覆盖整个三维空间？

对于n维情况，n个列向量如果相互独立——线性无关，则方程组有解；否则n个向量线性相关，无法充满n维空间，方程组未必有解

奇异矩阵/不可逆矩阵

三个列向量无论怎么组合也得不到平面外的向量b。此时矩阵A为奇异阵或称不可逆矩阵。

也可以理解为系数矩阵里列（行）向量不是相互独立的

在矩阵A不可逆条件下，不是所有的b都能令方程Ax=b有解。

二、矩阵消元

高斯消元法（Gauss elimination）就是通过对方程组中的某两个方程进行适当的数乘和加（jian）和（fa），以达到将某一未知数系数变为零，从而削减未知数个数的目的。

我们将矩阵左上角的1称之为“主元一”（the first pivot），第一步要通过消元将第一列中除了主元之外的数字均变化为0。操作方法就是用之后的每一行减去第一行的适当倍数，此例中第二行应减去第一行的3倍。之后应对第三行做类似操作，本例中三行第一列数字已经为0，故不用进行操作。

处在第二行第二列的主元二为2，因此用第三行减去第二行的两倍进行消元，得到第三个主元为5。

矩阵A为可逆矩阵，消元结束后得到上三角阵U（Uppertriangular matrix），其左侧下半部分的元素均为0，而主元1,2,5分列在U的对角线上。主元之积即行列式的值。

需要说明的是，主元不能为0，如果恰好消元至某行，0出现在了主元的位置上，应当通过与下方一行进行“行交换”使得非零数字出现在主元位置上。如果0出现在了主元位置上，并且下方没有对等位置为非0数字的行，则消元终止，并证明矩阵A为不可逆矩阵，且线性方程组没有唯一解。

消元矩阵

左行

矩阵左乘行向量则是对矩阵的行向量进行线性组合

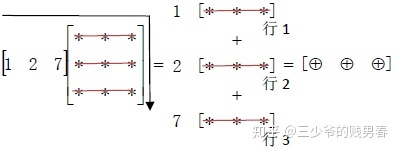
右列

系数矩阵乘以未知数向量，相当于对系数矩阵的列向量进行线性组合

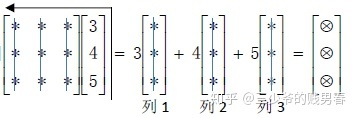
置换矩阵

当应用消元法求解方程组的时候我们需要通过行交换将0从主元位置移走。左乘一个置换阵可以实现行交换的操作

左乘置换矩阵可以完成原矩阵的行变换，右乘置换矩阵则为列变换

置换矩阵P是通过对单位阵进行“行交换”得到的。对于nxn矩阵存在着n!个置换矩阵。置换矩阵具有特殊性质 $P^{-1}=P^{T}$ 即 $P^{T}P=I$

逆矩阵

如果矩阵A是方阵，若存在逆矩阵 A−1 ，使得 $A^{^{-1}}A=I=AA^{^{-1}}$ （左逆矩阵等于右逆矩阵）。我们称矩阵A可逆（invertible）或者矩阵A非奇异（nonsingular）。

反之，如果A为奇异（singular），则其没有逆矩阵。它的行列式为0。另一个等价的说法是，A为奇异阵，则方程Ax=0存在非零解x。例如：

$\begin{bmatrix} 1 &3 \\2 & 6 \end{bmatrix}\begin{bmatrix} -3\\1 \end{bmatrix}=\begin{bmatrix} 0\\0 \end{bmatrix}$

在这个二阶矩阵的例子中，两个列向量排列在同一方向上。不可逆矩阵中总有列向量对生成线性组合没有贡献，等价的说法还有：不可逆矩阵的列向量可以通过线性组合得到0。

换而言之，若矩阵A存在逆矩阵，则方程Ax=0只有零解。证明：反设其存在非零解x，则有

$x=(A^{^{-1}}A)x=A^{^{-1}}Ax=A^{^{-1}}0=0$ ，矛盾；

对于可逆矩阵，求它的逆矩阵是一个重要的问题。

从“列操作”的角度来看，求逆矩阵过程其实和求Ax=b相同，只是这里x为矩阵A−1 的第j列，而b为单位阵I 的第j列。

消元矩阵之逆矩阵的实施效果就是抵消原矩阵的消元操作。消元矩阵实现了对原矩阵A的操作

三、矩阵的运算

标准方法（行*列）

矩阵乘法的标准计算方法是通过矩阵A第i行的行向量和矩阵B 第j列的列向量点积得到cij。

线性代数笔记3——向量2（点积） - 我是8位的 - 博客园 (cnblogs.com)

本质上矩阵的代数运算就是线性方程组的运算

阵乘法可以视为给线性方程组做变量替换

列操作

列操作是指矩阵C的第j列是通过矩阵A乘以矩阵B第j列的列向量得到的。这表明矩阵C的列向量是矩阵A列向量的线性组合

行操作

行操作是指矩阵C的第i行是通过矩阵A的第i行乘以矩阵B得到的。这表明矩阵C的行向量是矩阵B行向量的线性组合。

高斯-若尔当消元法

求逆相当于两组方程：

Gauss-Jordan消元法可以同时处理两个方程：

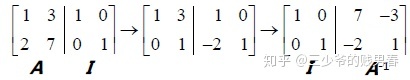
该过程可以理解为先对A进行一系列消元操作，相当于左乘消元矩阵E

$E\begin{bmatrix} A &| I \end{bmatrix}=\begin{bmatrix} EA &| EI \end{bmatrix}=\begin{bmatrix} I & |A^{-1} \end{bmatrix}$

由EA=I 可知E就是A的逆矩阵

四、空间

向量空间

我们可以对向量进行所谓“线性运算”，即通过加和（v+w）与数乘运算（3v）得到向量的线性组合。向量空间对线性运算封闭，即空间内向量进行线性运算得到的向量仍在空间之内。

R2即为向量空间，它是具有两个实数分量的所有向量（二维实向量）的集合。

向量 $\begin{bmatrix} a\\b \end{bmatrix}$ 的图像是从原点出发到点(a,b)的箭头，其中第一分量a为横轴坐标，第二分量b为纵轴坐标。空间R2的图像为整个x-y平面。

所有向量空间必然包含零向量，因为任何向量数乘0或者加上反向量都会得到零向量，而因为向量空间对线性运算封闭，所以零向量必属于向量空间。

R3是向量空间，它是具有三个实数分量的所有向量的集合。

Rn是向量空间，它是具有n个实数分量的所有向量的集合。

反例：R2中的第一象限则不是一个向量空间。

子空间

包含于向量空间之内的一个向量空间称为原向量空间的一个子空间。例如用实数c数乘R2空间中向量v所得到的向量集合就是R2空间的一个子空间，其图像为二维平面上穿过原点的一条直线，它对于线性运算封闭。

反例：R2中不穿过原点的直线就不是向量空间。子空间必须包含零向量，原因就是数乘0得到的零向量必须处于子空间中。

“子空间”为包含于向量空间内的一个向量空间。它是原向量空间的一个子集，而且本身也满足向量空间的要求。

R2的子空间包括：

R2空间本身
过原点的一条直线（这是R2空间中的一条直线，与R1空间有区别）
原点仅包含0向量 Z

R3的子空间包括：

R3空间本身 3维
过原点的一个平面 2维
过原点的一条直线 1维
原点仅包含0向量 Z

列空间

矩阵A的列空间C(A)是其列向量的所有线性组合所构成的空间

求解Ax=b的问题，对于给定的矩阵A，对于任意的b都能得到解么？

如果 A= $\begin{bmatrix} 1 &1 &2 \\2 & 1 & 2\\2 & 1 &4 \\ 4& 1 &5 \end{bmatrix}$

显然并不是所有的b都能保证Ax=b有解，因为它有4个线性方程而只有3个未知数，矩阵A列向量的线性组合无法充满R4，因此如果b不能被表示为A列向量的线性组合时，方程是无解的。只有当b在矩阵A列空间C(A)里时，x才有解。

对于我们所给定的矩阵A，由于列向量不是线性无关的，第三个列向量为前两个列向量之和，所以尽管有3个列向量，但是只有2个对张成向量空间有贡献。矩阵A的列空间为R4(为什么R4，可以理解为列向量 $\begin{bmatrix} 1\\ 2\\ 3\\ 4 \end{bmatrix}$ 是x,y,z,四维）内一个二维子空间。

零空间

矩阵A的零空间N(A)是指满足Ax=0的所有解的集合。

对于所给定这个矩阵A $\begin{bmatrix} 1 &1 &2 \\2 & 1 & 2\\2 & 1 &4 \\ 4& 1 &5 \end{bmatrix}$ ，其列向量含有4个分量，因此列空间是空间R4的子空间，x为含有3个分量的向量，故矩阵A的零空间是R3的子空间。对于mxn矩阵，列空间为Rm的子空间，零空间为Rn空间的子空间。

本例中矩阵A的零空间N(A)为包含 $\begin{bmatrix} 1\\ 1\\ -1 \end{bmatrix}$ 的任何倍数的集合，因为很容易看到第一列向量（1）和第二列向量（1）相加减去第三列向量（-1）为零。此零空间为R3中的一条直线。

b值的影响

若方程变为 $\begin{bmatrix} 1 &1 &2 \\ 2& 1 &3 \\ 3& 1 &4 \\ 4& 1 &5 \end{bmatrix}\begin{bmatrix} x1\\ x2\\ x3 \end{bmatrix}=\begin{bmatrix} 1\\ 2\\ 3\\ 4 \end{bmatrix}$ ，则其解集不能构成一个子空间。零向量并不在这个集合内。解集是空间R3内过 $\begin{bmatrix} 1\\ 0\\ 0 \end{bmatrix}$ 和 $\begin{bmatrix} 0\\ -1\\ 1 \end{bmatrix}$ 的一个平面，但是并不穿过原点 $\begin{bmatrix} 0\\ 0\\ 0 \end{bmatrix}$ 。