傅里叶对偶性

时域和频域的采样、周期性以及它们的相互关系

这段话描述了时域和频域之间的采样、周期性以及它们的相互关系。核心概念是傅里叶变换的对偶性，即时域和频域之间的关系。我们逐步解析这段话的每一部分：

1. 时域采样的影响

首先，时域的采样会导致频域中变得周期性。这意味着，如果我们对信号在时域上进行采样，它的频谱在频域上将呈现周期性重复。这个周期性与采样间隔 $\Delta t$ 直接相关。

• 采样间隔 $\Delta t$：这是时域中两个采样点之间的时间间隔。
• 采样频率 $f_s=\frac{1}{\Delta t}$：这是每秒采样的次数。也就是说，采样频率 $f_s$ 是采样间隔的倒数，采样频率越高，采样点之间的时间间隔 $\Delta t$ 就越小。

如果用弧度表示采样频率，可以写成：

$${\omega }_s=\frac{2\pi }{\Delta t}$$

其中 ${\omega }_s$ 是采样频率的角频率表示形式。

2. 对偶性：频域采样与时域周期性

傅里叶变换的对偶性告诉我们，如果对一个信号的频域进行采样，那么时域就会表现为周期性。这是时域和频域之间对称性质的一种体现。

具体来说：

• 如果时域被采样，频域会变得周期性，而这个周期由采样间隔 $\Delta t$ 决定。
• 如果频域被采样，时域会变得周期性，而这个周期由频域采样间隔 $\Delta \omega$ 决定。

3. 时域周期性的推导

当我们在频域中对信号进行采样时，时域信号会表现出周期性。这个周期 $T$ 是时域信号的重复周期，它与频域采样间隔 $\Delta \omega$ 有直接关系。

• 频域采样间隔 $\Delta \omega$：频域上两个频率点之间的间隔，定义为 $\Delta \omega =2\pi \Delta f$，其中 $\Delta f$ 是频率间隔。
• 时域周期 $T$：时域中的周期是与频域采样间隔成反比的。具体来说，如果我们在频域中采样，时域中的周期 $T$ 可以通过以下公式表示：

$$T=N\Delta t$$

这里 $N$ 是时域中采样点的总数，$\Delta t$ 是时域中每个采样点之间的间隔。因此，时域的周期 $T$ 等于采样点的数量 $N$ 乘以每个采样点的间隔 $\Delta t$。

4. 时域中的周期性样本数量

这意味着，如果我们对频域信号进行采样，当我们对采样频谱进行逆傅里叶变换时，时域中的信号会变成周期性的。这个周期是 $N$ 个样本，代表了时域信号的重复长度。

换句话说，频域的采样会在时域中引入周期性，且这个周期与时域中的采样点数量有关。当你对离散的频域信号进行逆变换时，时域信号会每隔 $N$ 个样本重复一次。

总结

• 时域采样导致频域周期性，周期与采样间隔 $\Delta t$ 相关。
• 频域采样导致时域周期性，时域的周期为 $T=N\Delta t$，即 $N$ 个样本的长度。
• 傅里叶变换的对偶性：时域和频域的采样/周期性具有对称性，时域采样对应频域周期，频域采样对应时域周期。

这种对偶关系是信号处理的核心概念，通过理解时域和频域之间的这种相互作用，可以解释很多离散信号处理中的现象。

import numpy as np
import matplotlib.pyplot as plt

# Parameters
fs = 1  # Sampling frequency in Hz
T = 1/fs  # Sampling period
N = 8  # Number of samples
t = np.linspace(0, (N-1)*T, N)  # Time vector

# Generate a discrete-time signal (e.g., a cosine wave)
f_signal = 0.1  # Frequency of the signal in Hz
x_n = np.cos(2 * np.pi * f_signal * t)  # Discrete-time signal

# Visualize the discrete-time signal and its periodic extension
plt.figure(figsize=(10, 6))

# Plot the original sampled signal
plt.stem(t, x_n, 'r', basefmt=" ", markerfmt='ro', label='Sampled Signal')
plt.plot(t, x_n, 'b-', label='Underlying Signal')

# Extend the signal periodically
t_extended = np.linspace(0, 2 * (N-1)*T, 2*N)
x_extended = np.tile(x_n, 2)  # Periodic extension of the signal
plt.stem(t_extended, x_extended, 'g', basefmt=" ", markerfmt='go', label='Periodic Extension')

# Plot labels and titles
plt.title('Discrete-Time Signal and Periodic Extension (N samples)')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.grid(True)
plt.legend()

# Show plot
plt.show()

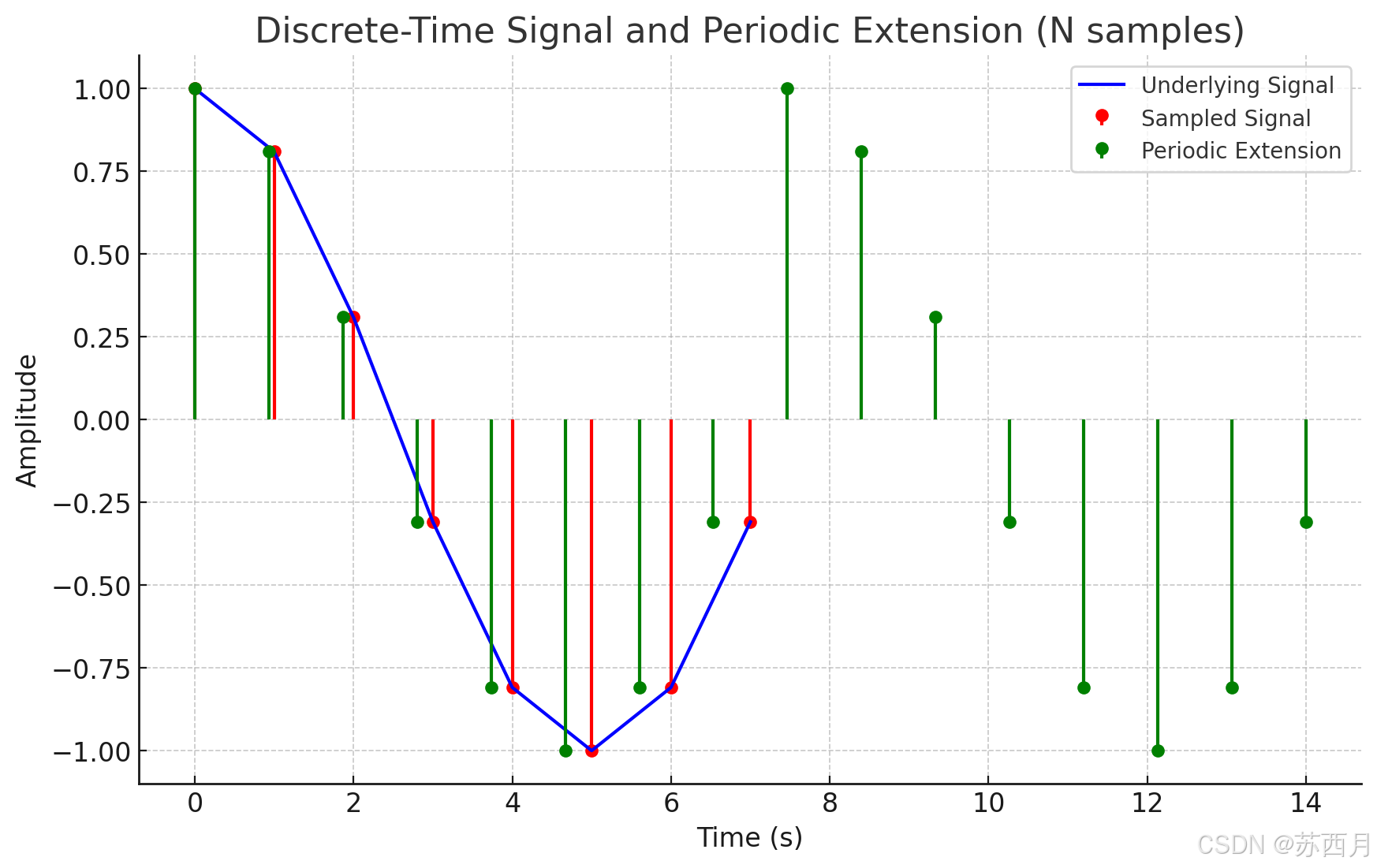
图中的内容：
蓝色曲线（Underlying Signal）： 代表了生成的原始离散时间信号（例如，余弦波）。
红色竖线和圆点（Sampled Signal）： 表示离散信号的采样点，即在时域中每个采样时刻的信号值。
绿色竖线和圆点（Periodic Extension）： 表示信号的周期性扩展。由于离散时间信号的频域是周期性的，逆傅里叶变换后的时域信号也会周期性重复。这部分绿色的点是对原始信号的一个周期性复制。