一、三角函数
1.公式
同角三角函数间的基本关系式:
·平方关系:
sin^2(α)+cos^2(α)=1; tan^2(α)+1=sec^2(α);cot^2(α)+1=csc^2(α)
·商的关系:
tanα=sinα/cosα cotα=cosα/sinα
·倒数关系:
tanα·cotα=1; sinα·cscα=1; cosα·secα=1
三角函数恒等变形公式:
·两角和与差的三角函数:
cos(α+β)=cosα·cosβ-sinα·sinβ
cos(α-β)=cosα·cosβ+sinα·sinβ
sin(α±β)=sinα·cosβ±cosα·sinβ
tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)
tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)
倍角公式:
sin(2α)=2sinα·cosα
cos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)
tan(2α)=2tanα/[1-tan^2(α)]
·半角公式:
sin^2(α/2)=(1-cosα)/2
cos^2(α/2)=(1+cosα)/2
tan^2(α/2)=(1-cosα)/(1+cosα)
tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα
·万能公式:
sinα=2tan(α/2)/[1+tan^2(α/2)]
cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]
tanα=2tan(α/2)/[1-tan^2(α/2)]
·积化和差公式:
sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]
cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]
cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]
sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]
·和差化积公式:
sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]
sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]
cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]
cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]
2.特殊角的三角函数值

只需记住这两个特殊的直角三角形的边角关系,依照三角函数的定义即可推出上面的三角值。
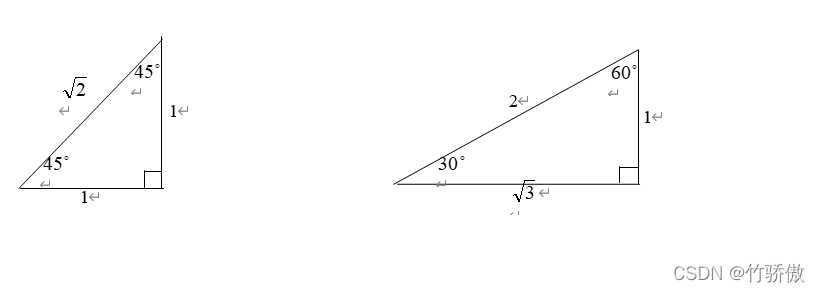
3诱导公式:
| 函数 角A | sin | cos | tg | ctg |
| -α | -sinα | cosα | -tgα | -ctgα |
| 90°-α | cosα | sinα | ctgα | tgα |
| 90°+α | cosα | -sinα | -ctgα | -tgα |
| 180°-α | sinα | -cosα | -tgα | -ctgα |
| 180°+α | -sinα | -cosα | tgα | ctgα |
| 270°-α | -cosα | -sinα | ctgα | tgα |
| 270°+α | -cosα | sinα | -ctgα | -tgα |
| 360°-α | -sinα | cosα | -tgα | -ctgα |
| 360°+α | sinα | cosα | tgα | ctgα |
记忆规律: 竖变横不变(奇变偶不变),符号看象限(一全,二正弦割,三切,四余弦割 )
即第一象限全是正的,第二象限正弦、正割是正的,第三象限正切是正的,第四象限余弦、余割是正的)
二、一元二次函数、方程和不等式

三、因式分解与乘法公式

四、等差数列和等比数列


五、常用几何公式
| 平面图形 | ||
| 名称 | 符号 | 周长C和面积S |
| 正方形 | a—边长 | C=4a |
| 长方形 | a和b-边长 | C=2(a+b) |
| 三角形 | a,b,c-三边长 | S=ah/2 |
| 平行四边形 | a,b-边长 | S=ah |
| 菱形 | a-边长 | S=Dd/2 |
| 梯形 | a和b-上、下底长 | S=(a+b)h/2 |
| 圆 | r-半径 | C=πd=2πr |
| 扇形 | r—扇形半径 | C=2r+2πr×(a/360) |
| 圆环 | R-外圆半径 | S=π(R2-r2) |
| 椭圆 | D-长轴 | S=πDd/4 |
| 立方图形 | ||
| 名称 | 符号 | 表面积S和体积V |
| 正方体 | a-边长 | S=6a2 |
| 长方体 | a-长 | S=2(ab+ac+bc) |
| 圆柱 | r-底半径 | C=2πr |
| 圆锥 | r-底半径 | V=πr2h/3 |
| 球 | r-半径 | V=4/3πr3 =πd3/6 S=4πr2 =πd2 |
基本初等函数


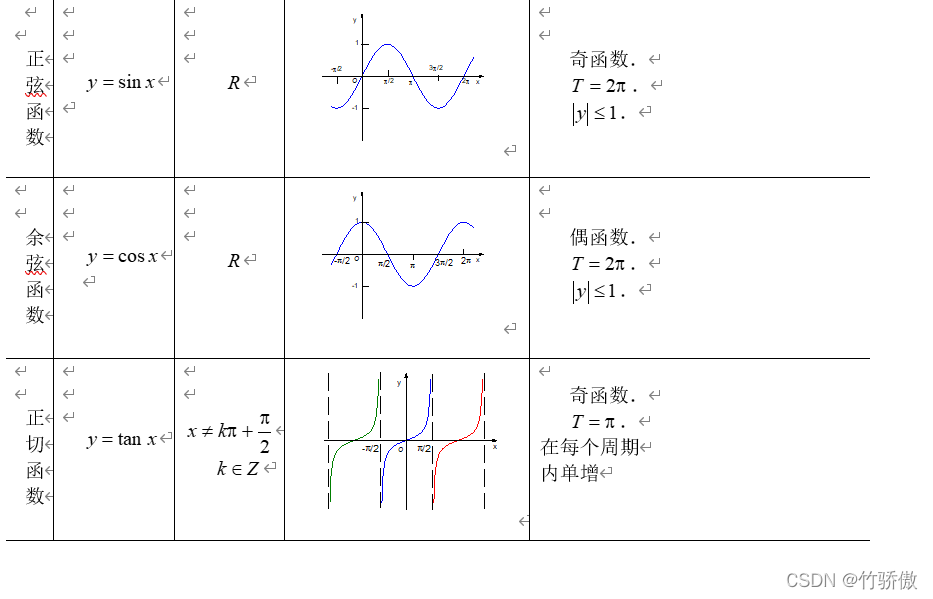
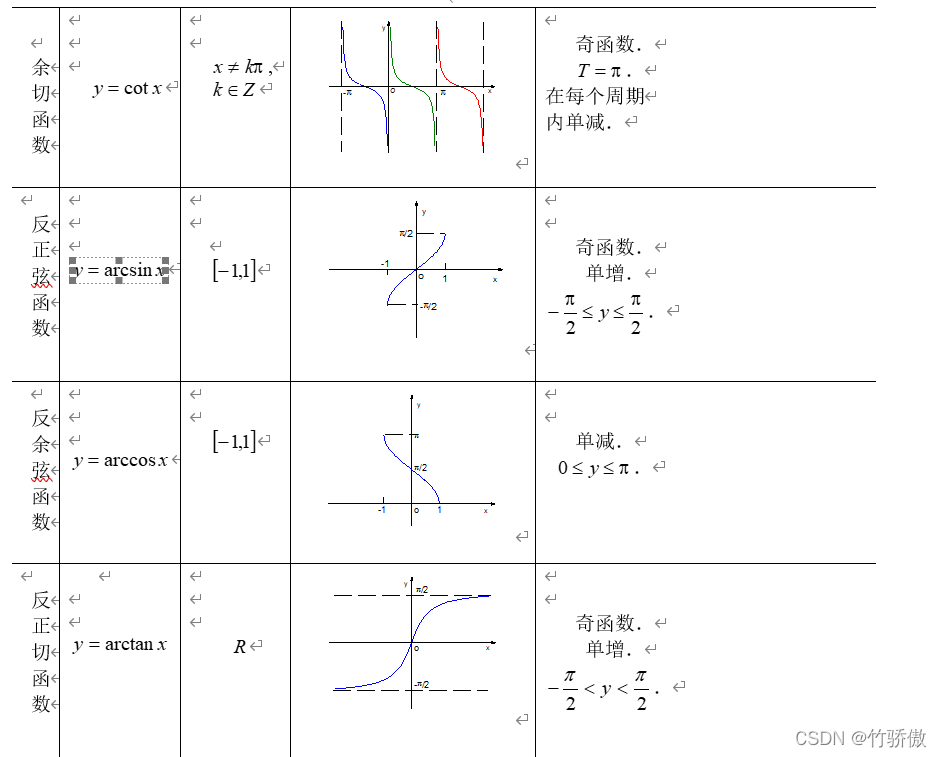


























 3301
3301

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










