文章探讨了零点问题，强调了零点定理在证明存在性和唯一性中的应用，以及单调性如何影响零点的数量。此外，还提到了实系数奇数次方程至少有一个实根的性质。微分不等式主要关注函数的单调性和最值问题，同时也讨论了凹凸性和中值定理的相关应用。
重点
零点问题
大题
零点定理，证存在性
单调性，证唯一性
小题工具
罗尔原话
实系数奇次方程至少有一个实根
微分不等式
函数性态
常数变量化
中值定理
零点问题
零点定理
当 f ( x ) 在 [ a , b ] 上连续，且 f ( a ) ⋅ f ( b ) < 0 时 \text {当 }f(x)\text 在 [a,b]\text {上连续，且} f(a) \cdot f(b)<0 \text { 时} 当 f(x)在[a,b]上连续，且f(a)⋅f(b)<0 时，则 f ( x ) = 0 f(x)=0 f(x)=0，在 ( a , b ) (a,b) (a,b)内至少有一个根
推广的零点定理: 若 f ( x ) 在 ( a , b ) 内连续 , lim x → a + f ( x ) = α , lim x → b f ( x ) = β 若 f(x) 在 (a, b) 内连 续, \lim _{x \rightarrow a^{+}} f(x)=\alpha, \lim _{x \rightarrow b} f(x)=\beta 若f(x)在(a,b)内连续,limx→a+f(x)=α,limx→bf(x)=β ,
且 α ⋅ β < 0 \alpha \cdot \beta<0 α⋅β<0
则 f ( x ) = 0 在 ( a , b ) 则 f(x)=0 在 (a, b) 则f(x)=0在(a,b) 内至少有一个根,
这里 a , b , α , β a, b, \alpha, \beta a,b,α,β 可以是有限数, 也可以是无穷大
单调性
罗尔原话
若 f ( n ) ( x ) = 0 至多有 k 个根, 则 f ( x ) = 0 至多有 k + n 个根 \text { 若 } f^{(n)}(x)=0 \text { 至多有 } k \text { 个根, 则 } f(x)=0 \text { 至多有 } k+n \text { 个根 } 若 f(n)(x)=0 至多有 k 个根, 则 f(x)=0 至多有 k+n 个根
阶数降多少，根数加多少
只用不证
实系数奇数方程至少一个实根
x 2 n + 1 + a 1 x 2 n + ⋯ + a 2 n x + a 2 n + 1 = 0 x^{2 n+1}+a_{1} x^{2 n}+\cdots+a_{2 n} x+a_{2 n+1}=0 x2n+1+a1x2n+⋯+a2nx+a2n+1=0
微分不等式
函数性态
单调性（主流考法）
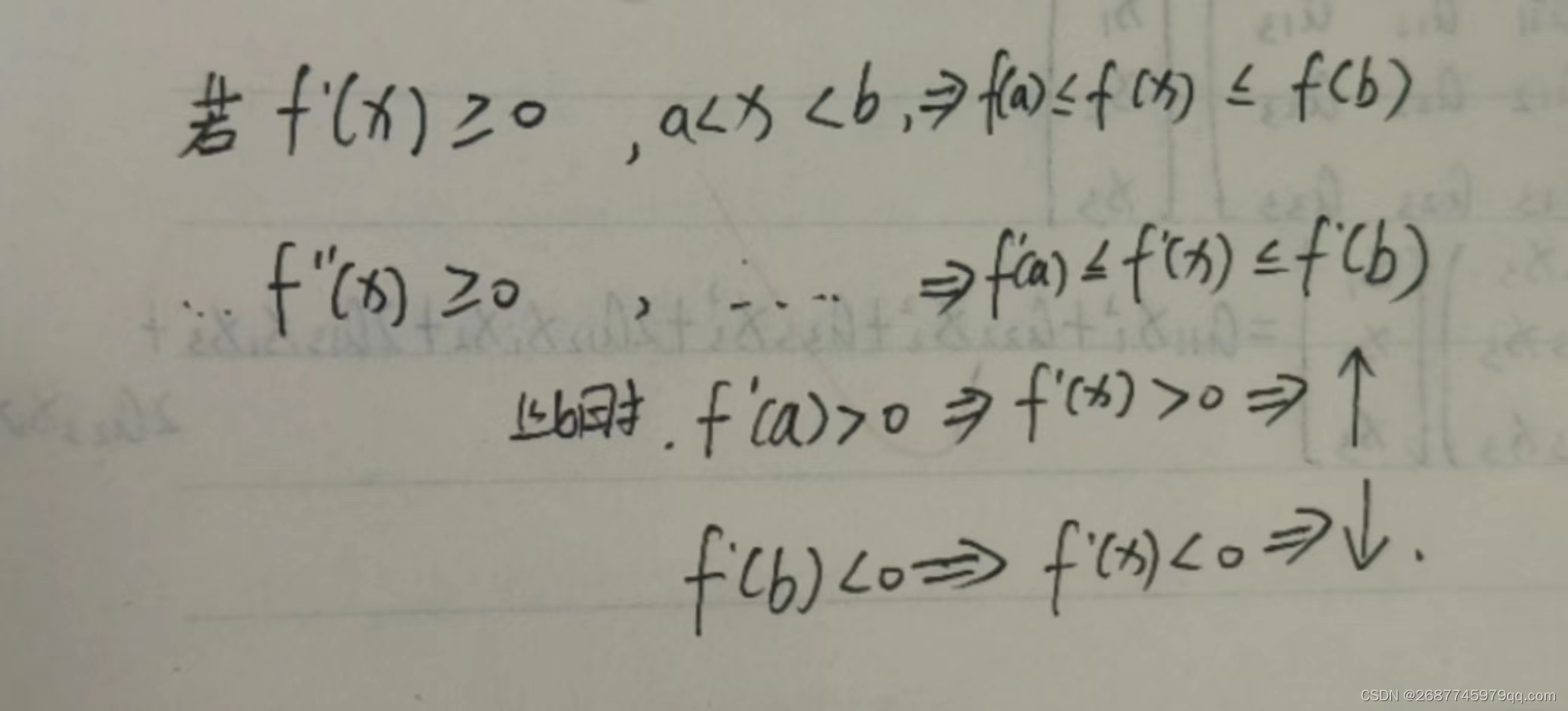
最值（重要）
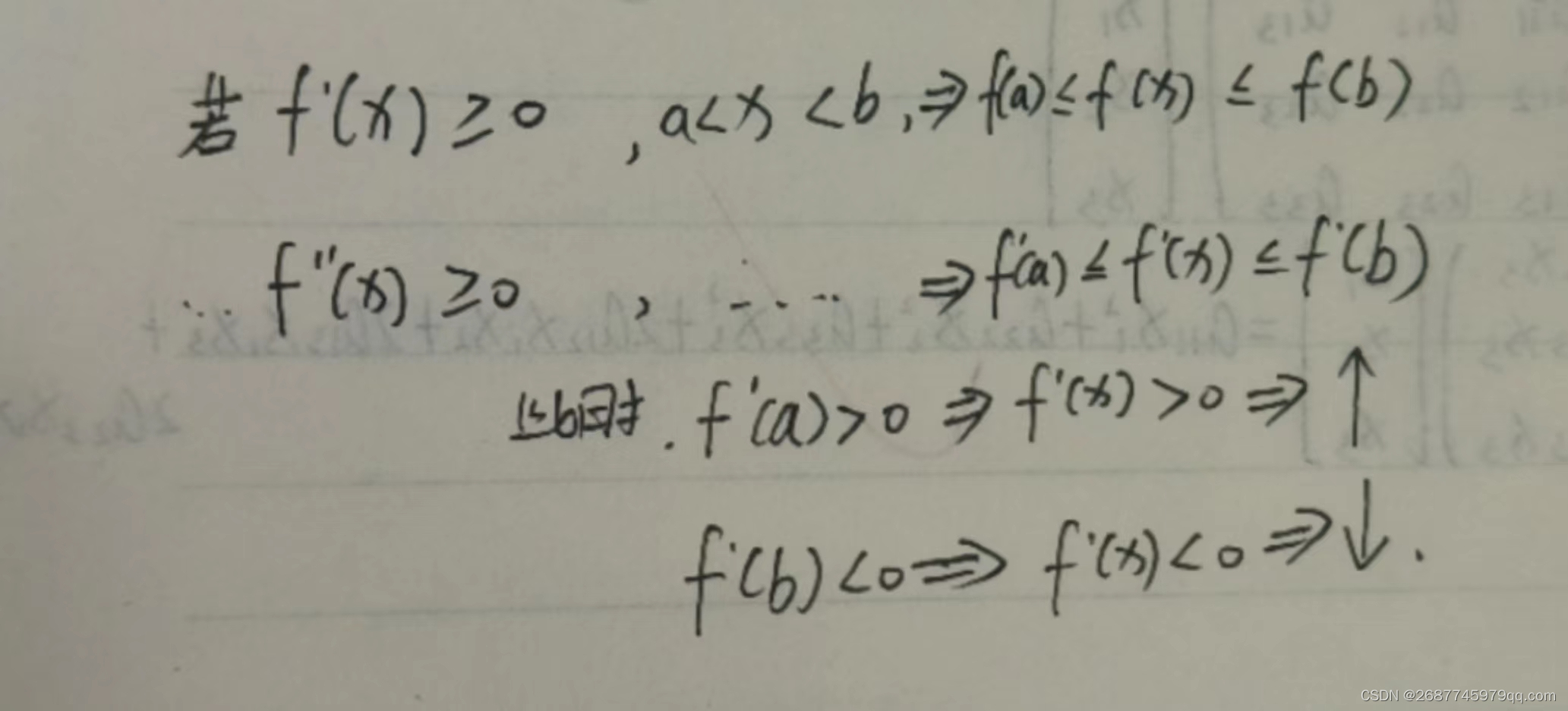
凹凸性
常数变量化
中值定理或泰勒
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
