重点
概念
重中之重的一讲
考研对概念要求非常深刻
不定积分
原函数与不定积分
不定积分存在定理
- 连续函数必有原函数
- 振荡间断点可能有原函数
- 含第一类间断点、无穷间断点没有
定积分
概念
存在定理
性质
不定积分
概念
性质
求导公式
计算
基本积分公式
凑微分法
换元法
分部积分法
有理函数积分
考点

概念
不定积分
原函数
一个
∀ x ∈ I , F ( x ) ′ = f ( x ) \forall x \in I ,F(x)'=f(x) ∀x∈I,F(x)′=f(x)
全体
F ( x ) ′ = f ( x ) + C F(x)'=f(x)+C F(x)′=f(x)+C
不定积分
∫ f ( x ) d x = F ( x ) + C \int f(x) \mathrm{d} x=F(x)+C ∫f(x)dx=F(x)+C 为 f ( x ) f(x) f(x) 在区间 I I I 上的不定积分
存在定理
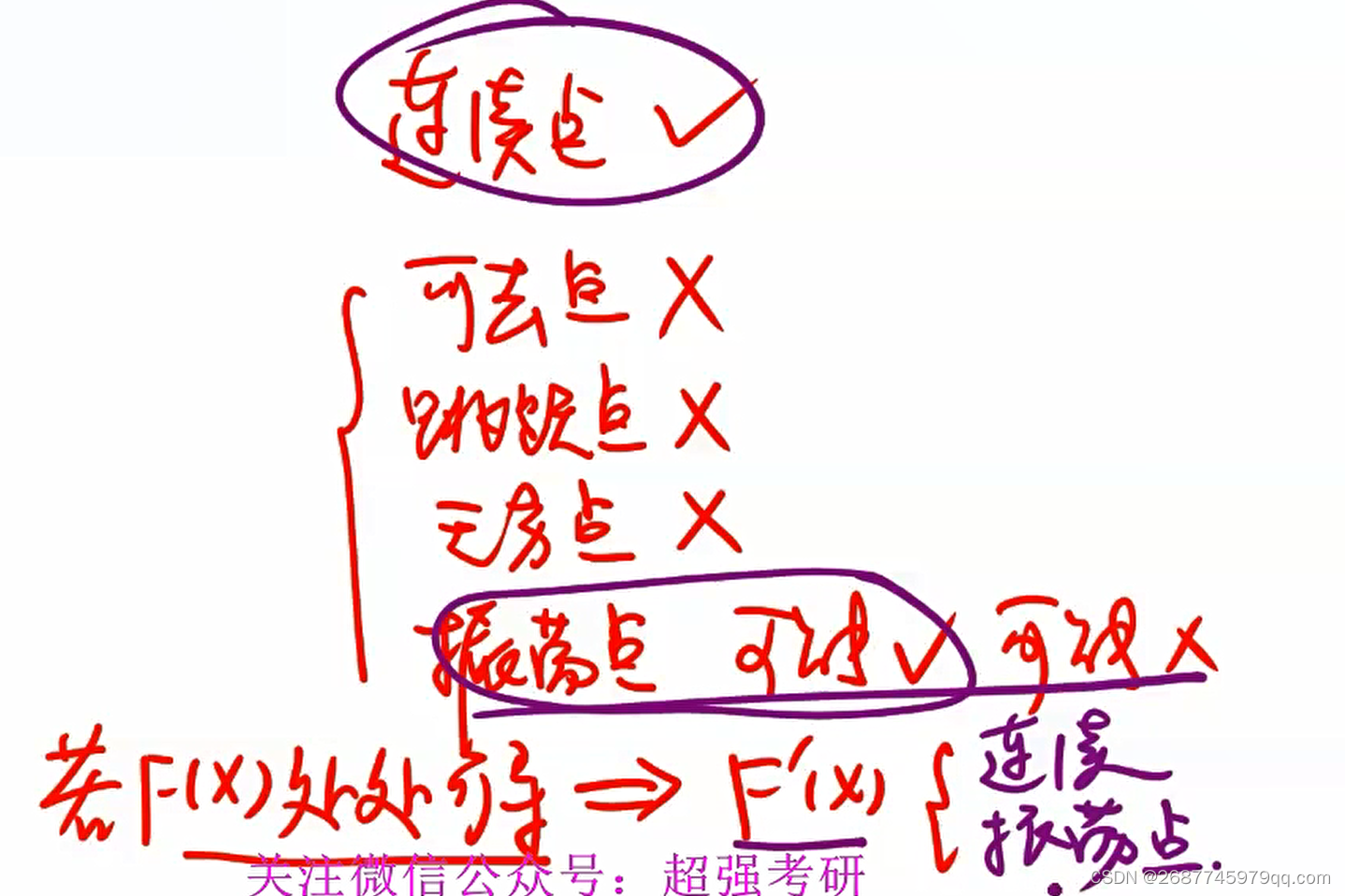
连续函数必有原函数

振荡间断点可能有原函数
含第一类间断点、无穷间断点没有

定积分
黎曼积分
分割、近似、求和、取极限
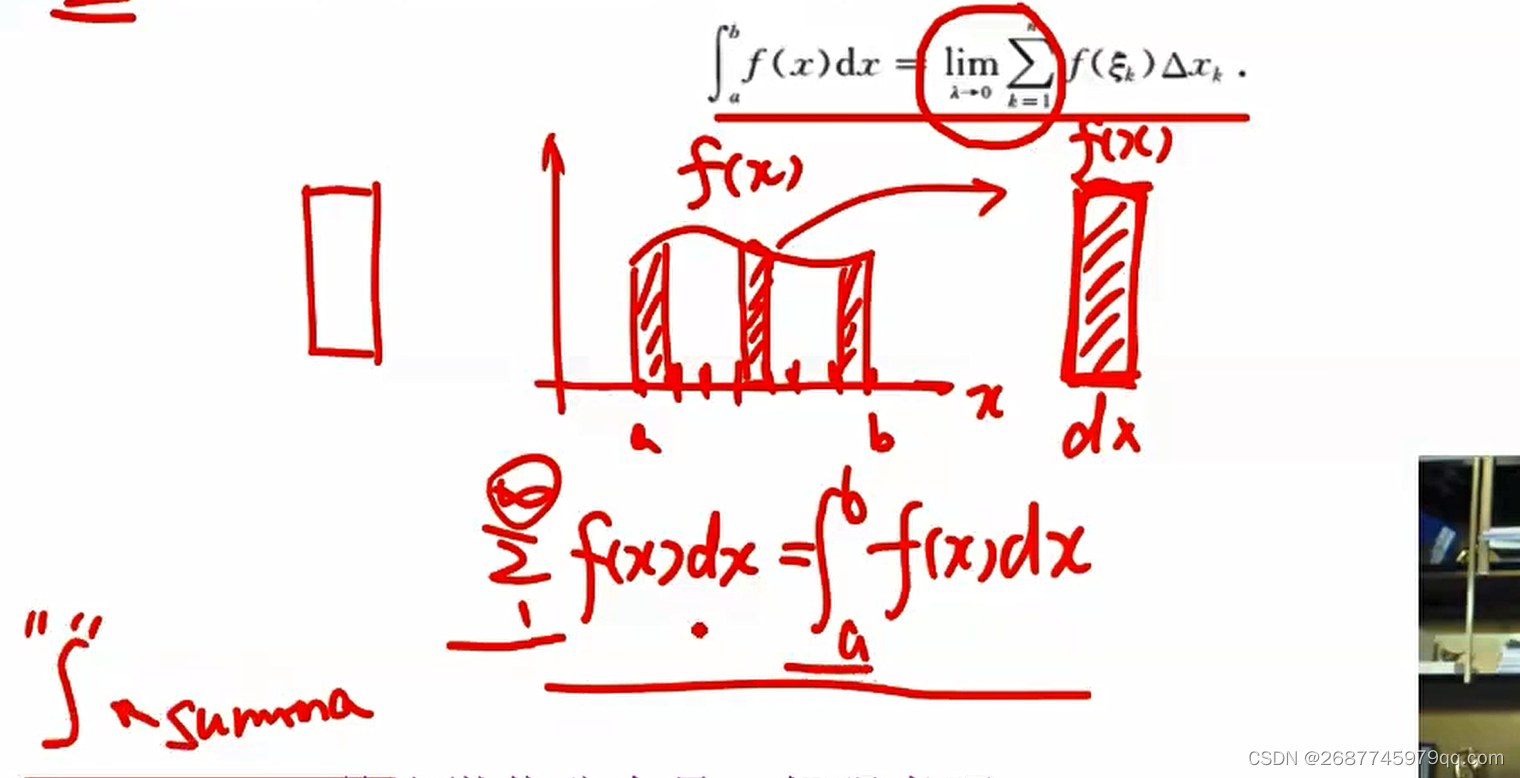
精准定义
${\huge {\color{Purple} \int_{a}^{b} f(x) \mathrm{d} x=\lim {n \rightarrow \infty} \sum{i=1}^{n} f\left(a+\frac{b-a}{n} i\right) \frac{b-a}{n}} } $
怎么用
-
提$\frac{1}{n} $
-
凑$\frac{i}{n} $
-
由于 i n = 0 + 1 − 0 n i , 故 i n 可以读作 0 到 1 上的 x \text {由于 } \frac{i}{n}=0+\frac{1-0}{n} i \text {, 故 }\frac{i}{n} \text { 可以读作 0 到 } 1 \text { 上的 } x 由于 ni=0+n1−0i, 故 ni 可以读作 0 到 1 上的 x
且 1 n = 1 − 0 n \text {且 } \frac{1}{n}=\frac{1-0}{n} 且 n1=n1−0
读作“0 到 1 上的 d x ”, 于是,“凑定义”完毕 \text {读作“0 到 } 1 \text { 上的 } \mathrm{d} x \text { ”, 于是,“凑定义”完毕 } 读作“0 到 1 上的 dx ”, 于是,“凑定义”完毕

【注】
-
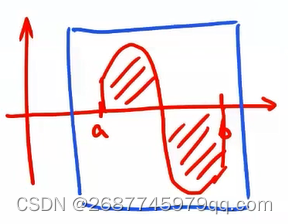
图在 x x x轴下面时,定积分值为负
-
a < b 时, d x > 0 ; a > b 时, d x < 0 a<b \text { 时, } \mathrm{d} x>0 ; a>b \text { 时, } \mathrm{d} x<0 a<b 时, dx>0;a>b 时, dx<0
-
∫ a b f ( x ) d x = − ∫ b a f ( x ) d x \int_{a}^{b} f(x) d x=-\int_{b}^{a} f(x) d x ∫abf(x)dx=−∫baf(x)dx
存在定理
连续存在
单调存在
有界,有限个间断点存在
可去,跳跃、振荡(不包含无界振荡)
可积函数必有界
性质
可加性
无论 a , b , c 的大小如何, 总有 ∫ a b f ( x ) d x = ∫ a c f ( x ) d x + ∫ a b f ( x ) d x \text { 无论 } a, b, c \text { 的大小如何, 总有 } \int_{a}^{b} f(x) \mathrm{d} x=\int_{a}^{c} f(x) \mathrm{d} x+\int_{a}^{b} f(x) \mathrm{d} x 无论 a,b,c 的大小如何, 总有 ∫abf(x)dx=∫acf(x)dx+∫abf(x)dx
首尾呼应即可
保号性
若在区间 [ a , b ] 上 f ( x ) ⩽ g ( x ) , 则有 ∫ a b f ( x ) d x ⩽ ∫ a b g ( x ) d x \text { 若在区间 }[a, b] \text { 上 } f(x) \leqslant g(x) \text {, 则有 } \int_{a}^{b} f(x) \mathrm{d} x \leqslant \int_{a}^{b} g(x) \mathrm{d} x 若在区间 [a,b] 上 f(x)⩽g(x), 则有 ∫abf(x)dx⩽∫abg(x)dx
面积抵消小于不抵消
∣ ∫ a b f ( x ) d x ∣ ⩽ ∫ a b ∣ f ( x ) ∣ d x \left|\int_{a}^{b} f(x) \mathrm{d} x\right| \leqslant \int_{a}^{b}|f(x)| \mathrm{d} x ∫abf(x)dx ⩽∫ab∣f(x)∣dx
被积函数非负
设 f ( x ) 是 [ a , b ] 上非负的连续函数 , 只要 f ( x ) 不恒等于零 , 则必有 ∫ a b f ( x ) d x > 0 设 f(x) 是 [a, b] 上非负的连续函数, 只要 f(x) 不恒等于零, 则必有\int_{a}^{b} f(x) \mathrm{d} x>0 设f(x)是[a,b]上非负的连续函数,只要f(x)不恒等于零,则必有∫abf(x)dx>0
估值定理
设 M , m 分别是 f ( x ) 在 [ a , b ] 上的最大值和最小值 , L 为区间 [ a , b ] 的长度 , 则有 设 M, m 分别是 f(x) 在 [a, b] 上的最大值和最小值, L 为区间 [a, b] 的长度, 则有 设M,m分别是f(x)在[a,b]上的最大值和最小值,L为区间[a,b]的长度,则有 m L ⩽ ∫ a b f ( x ) d x ⩽ M L m L \leqslant \int_{a}^{b} f(x) \mathrm{d} x \leqslant M L mL⩽∫abf(x)dx⩽ML
将线推向面
中值定理
设 f ( x ) 在闭区间 [ a , b ] 上连续 , 则在 [ a , b ] 上至少存在一点 ξ , 使得 ∫ a b f ( x ) d x = f ( ξ ) ( b − a ) . 设 f(x) 在闭区间 [a, b] 上连续, 则在 [a, b] 上至少存在一点 \xi , 使得\int_{a}^{b} f(x) \mathrm{d} x=f(\xi)(b-a) . 设f(x)在闭区间[a,b]上连续,则在[a,b]上至少存在一点ξ,使得∫abf(x)dx=f(ξ)(b−a).
变限积分
概念
变上限积分函数
Φ ( x ) = ∫ a x f ( t ) d t ( a ⩽ x ⩽ b ) \Phi(x)=\int_{a}^{x} f(t) \mathrm{d} t(a \leqslant x \leqslant b) Φ(x)=∫axf(t)dt(a⩽x⩽b)
其中 x x x为求导变量, t t t为积分变量
换元要三换
性质
函数 f ( x ) 在 [ a , b ] 上可积 , 则函数 F ( x ) = ∫ a x f ( t ) d t 在 [ a , b ] 上连续 函数 f(x) 在 [a, b] 上可积, 则函数 F(x)=\int_{a}^{x} f(t) \mathrm{d} t 在 [a, b] 上连续 函数f(x)在[a,b]上可积,则函数F(x)=∫axf(t)dt在[a,b]上连续
函数 f ( x ) 在 [ a , b ] 上连续 , 则函数 F ( x ) = ∫ x f ( t ) d t 在 [ a , b ] 上可导 函数 f(x) 在 [a, b] 上连续,则函数 F(x)=\int^{x} f(t) \mathrm{d} t 在 [a, b] 上可导 函数f(x)在[a,b]上连续,则函数F(x)=∫xf(t)dt在[a,b]上可导
可导 → \to →连续 → \to →可积 → \to →有界
套上变限积分,性质升一级
证明
求导

反常积分
概念
定积分,区间有限,函数有界
破坏积分区间1·
无穷区间的反常积分
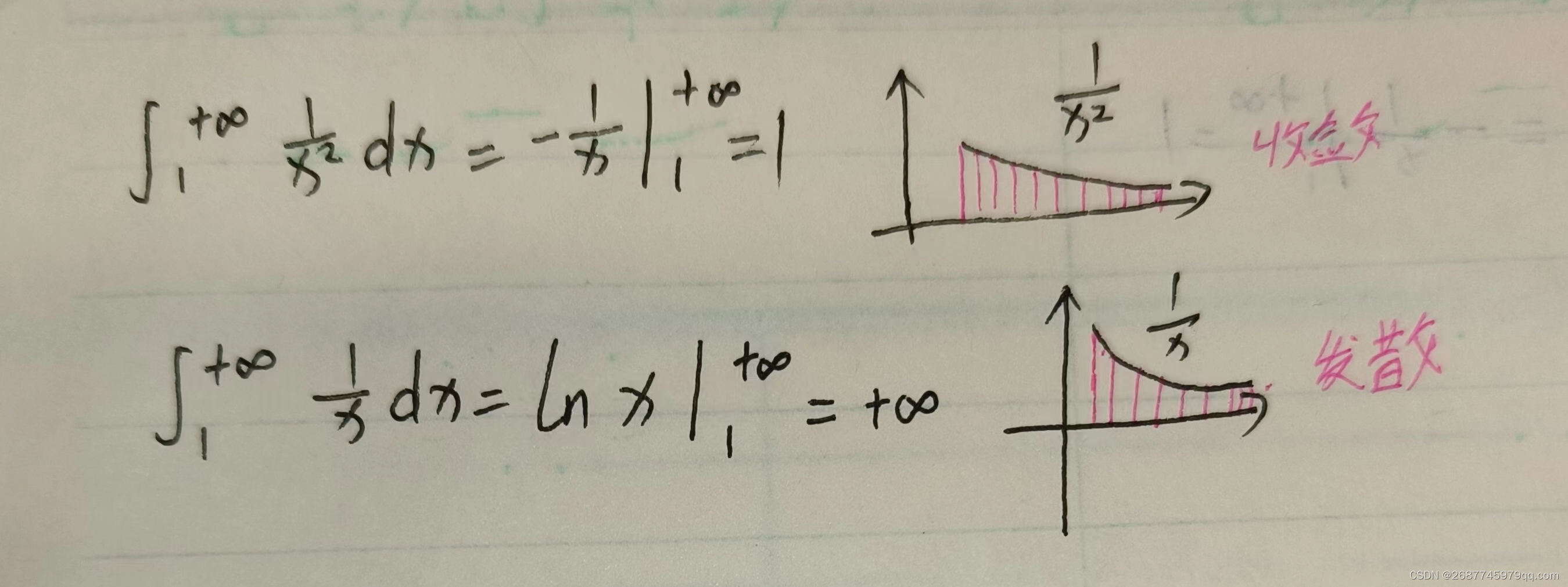
被积函数无界
无界函数的反常积分

反推不一定
∫ a + ∞ f ( x ) d x 收敛不一定能推出 lim x → + ∞ f ( x ) = 0 . \int_{a}^{+\infty} f(x) \mathrm{d} x \text { 收敛不一定能推出 } \lim _{x \rightarrow+\infty} f(x)=0 \text {. } ∫a+∞f(x)dx 收敛不一定能推出 limx→+∞f(x)=0.
如
f ( x ) = { n , x ∈ [ n , n + 1 n ⋅ 2 n ] , n = 1 , 2 , ⋯ 0 , 其他, {\LARGE f(x)=\left\{\begin{array}{ll}n, & x \in\left[n, n+\frac{1}{n \cdot 2^{n}}\right], n=1,2, \cdots \\0, & \text { 其他, }\end{array}\right.} f(x)=⎩ ⎨ ⎧n,0,x∈[n,n+n⋅2n1],n=1,2,⋯ 其他,
区间长度为 1 n ⋅ 2 n \frac{1}{n \cdot 2^{n}} n⋅2n1
高为 n n n
面积为 1 2 n \frac{1}{2^{n}} 2n1
此处区间收敛,函数发散
区间收敛程度较大 → \to →整体收敛
敛散性
无穷区间
定义


无界函数

敛散性判别

计算
常用积分公式
【注】
s e c x = 1 c o s x {\color{Red} {\Large secx=\frac{1}{cosx}}} secx=cosx1
c s c x = 1 s i n x {\color{Red} {\Large csc x=\frac{1}{sinx}}} cscx=sinx1
| ∫ x k d x = 1 k + 1 x k + 1 + C , k ≠ − 1 \int x^{k} \mathrm{~d} x=\frac{1}{k+1} x^{k+1}+C, k \neq-1 ∫xk dx=k+11xk+1+C,k=−1 | x k d x = d ( 1 k + 1 x k + 1 ) x^{k} d x=d\left(\frac{1}{k+1} x^{k+1}\right) xkdx=d(k+11xk+1) |
|---|---|
| ∫ 1 x 2 d x = − 1 x + C \int \frac{1}{x^{2}} \mathrm{~d} x=-\frac{1}{x}+C ∫x21 dx=−x1+C | 1 x 2 d x = d ( − 1 x ) \frac{1}{x^{2}} d x=d\left(-\frac{1}{x}\right) x21dx=d(−x1) |
| ∫ 1 x d x = 2 x + C \int \frac{1}{\sqrt{x}} \mathrm{~d} x=2 \sqrt{x}+C ∫x1 dx=2x+C | 1 x d x = d ( 2 x ) \frac{1}{\sqrt{x}} d x=d(2 \sqrt{x}) x1dx=d(2x) |
| ∫ 1 x d x = ln ∣ x ∣ + C \int \frac{1}{x} \mathrm{~d} x=\ln \vert x \vert+C ∫x1 dx=ln∣x∣+C | 1 x d x = d ( ln ∣ x ∣ ) \frac{1}{x} d x=d (\ln \vert x \vert) x1dx=d(ln∣x∣) |
| ∫ e x d x = e x + C \int \mathrm{e}^{x} \mathrm{~d} x=\mathrm{e}^{x}+C ∫ex dx=ex+C | e x d x = d ( e x ) e^{x} d x=d\left(e^{x}\right) exdx=d(ex) |
| ∫ a x d x = a x ln a + C , a > 0 且 a ≠ 1 \int a^{x} \mathrm{~d} x=\frac{a^{x}}{\ln a}+C, a>0 \text { 且 } a \neq 1 ∫ax dx=lnaax+C,a>0 且 a=1 | a x d x = d ( a x ln a ) a^{x} \mathrm{~d} x=d(\frac{a^{x}}{\ln a}) ax dx=d(lnaax) |
| ∫ sin x d x = − cos x + C \int \sin x \mathrm{~d} x=-\cos x+C ∫sinx dx=−cosx+C | sin x d x = d ( − cos x ) \sin x d x=d(-\cos x) sinxdx=d(−cosx) |
| ∫ cos x d x = sin x + C \int \cos x \mathrm{~d} x=\sin x+C ∫cosx dx=sinx+C | |
| ∫ tan x d x = − ln ∣ c o s x ∣ + C \int \tan x \mathrm{~d} x=-\ln \vert cos x \vert+C ∫tanx dx=−ln∣cosx∣+C | |
| ∫ cot x d x = ln ∣ sin x ∣ + C \int \cot x \mathrm{~d} x=\ln \vert\sin x \vert+C ∫cotx dx=ln∣sinx∣+C | |
| ∫ d x cos x = ∫ sec x d x = ln ∣ sec x + tan x ∣ + C \int \frac{\mathrm{d} x}{\cos x}=\int \sec x \mathrm{~d} x=\ln \vert \sec x+\tan x \vert +C ∫cosxdx=∫secx dx=ln∣secx+tanx∣+C | |
| ∫ d x sin x = ∫ csc x d x = ln ∣ c s c x − cot x ∣ + C \int \frac{\mathrm{d} x}{\sin x}=\int \csc x \mathrm{~d} x=\ln \vert csc x-\cot x\vert+C ∫sinxdx=∫cscx dx=ln∣cscx−cotx∣+C | |
| ∫ sec 2 x d x = tan x + C \int \sec ^{2} x \mathrm{~d} x=\tan x+C ∫sec2x dx=tanx+C | sec 2 x d x = d tan x \sec ^{2} x d x=d \tan x sec2xdx=dtanx |
| ∫ csc 2 x d x = − cot x + C \int \csc ^{2} x \mathrm{~d} x=-\cot x+C ∫csc2x dx=−cotx+C | |
| ∫ sec x tan x d x = sec x + C \int \sec x \tan x \mathrm{~d} x=\sec x+C ∫secxtanx dx=secx+C | |
| ∫ csc x cot x d x = − csc x + C \int \csc x \cot x \mathrm{~d} x=-\csc x+C ∫cscxcotx dx=−cscx+C | |
| ∫ 1 1 + x 2 d x = arctan x + C \int \frac{1}{1+x^{2}} \mathrm{~d} x=\arctan x+C ∫1+x21 dx=arctanx+C | |
| ∫ 1 a 2 + x 2 d x = 1 a arctan x a + C ( a > 0 ) \int \frac{1}{a^{2}+x^{2}} \mathrm{~d} x=\frac{1}{a} \arctan \frac{x}{a}+C(a>0) ∫a2+x21 dx=a1arctanax+C(a>0) | |
| ∫ 1 1 − x 2 d x = arcsin x + C \int \frac{1}{\sqrt{1-x^{2}}} \mathrm{~d} x=\arcsin x+C ∫1−x21 dx=arcsinx+C | |
| ∫ 1 a 2 − x 2 d x = arcsin x a + C ( a > 0 ) \int \frac{1}{\sqrt{a^{2}-x^{2}}} \mathrm{~d} x=\arcsin \frac{x}{a}+C(a>0) ∫a2−x21 dx=arcsinax+C(a>0) | |
| ∫ 1 x 2 + a 2 d x = ln ( x + x 2 + a 2 ) + C ( 常见 a = 1 ) \int \frac{1}{\sqrt{x^{2}+a^{2}}} \mathrm{~d} x=\ln \left(x+\sqrt{x^{2}+a^{2}}\right)+C(\text { 常见 } a=1) ∫x2+a21 dx=ln(x+x2+a2)+C( 常见 a=1) | |
| ∫ 1 x 2 − a 2 d x = ln ∣ x + x 2 − a 2 ∣ + C ( ∣ x ∣ > ∣ a ∣ ) \int \frac{1}{\sqrt{x^{2}-a^{2}}} \mathrm{~d} x=\ln \left \vert x+\sqrt{x^{2}-a^{2}}\right \vert +C(\vert x \vert > \vert a \vert) ∫x2−a21 dx=ln x+x2−a2 +C(∣x∣>∣a∣) | |
| ∫ 1 x 2 − a 2 d x = 1 2 a ln ∣ x − a x + a ∣ + C ( ∫ 1 a 2 − x 2 d x = 1 2 a ln ∣ x + a x − a ∣ + C ) \int \frac{1}{x^{2}-a^{2}} \mathrm{~d} x=\frac{1}{2 a} \ln \left \vert \frac{x-a}{x+a}\right \vert +C\left(\int \frac{1}{a^{2}-x^{2}} \mathrm{~d} x=\frac{1}{2 a} \ln \left \vert \frac{x+a}{x-a}\right \vert +C\right) ∫x2−a21 dx=2a1ln x+ax−a +C(∫a2−x21 dx=2a1ln x−ax+a +C) | |
| ∫ a 2 − x 2 d x = a 2 2 arcsin x a + x 2 a 2 − x 2 + C ( a > ∣ x ∣ ⩾ 0 ) \int \sqrt{a^{2}-x^{2}} \mathrm{~d} x=\frac{a^{2}}{2} \arcsin \frac{x}{a}+\frac{x}{2} \sqrt{a^{2}-x^{2}}+C(a> \vert x \vert\geqslant 0) ∫a2−x2 dx=2a2arcsinax+2xa2−x2+C(a>∣x∣⩾0) | |
| ∫ sin 2 x d x = x 2 − sin 2 x 4 + C ( sin 2 x = 1 − cos 2 x 2 ) \int \sin ^{2} x \mathrm{~d} x=\frac{x}{2}-\frac{\sin 2 x}{4}+C\left(\sin ^{2} x=\frac{1-\cos 2 x}{2}\right) ∫sin2x dx=2x−4sin2x+C(sin2x=21−cos2x) | |
| ∫ cos 2 x d x = x 2 + sin 2 x 4 + C ( cos 2 x = 1 + cos 2 x 2 ) \int \cos ^{2} x \mathrm{~d} x=\frac{x}{2}+\frac{\sin 2 x}{4}+C\left(\cos ^{2} x=\frac{1+\cos 2 x}{2}\right) ∫cos2x dx=2x+4sin2x+C(cos2x=21+cos2x) | |
| ∫ tan 2 x d x = tan x − x + C ( tan 2 x = sec 2 x − 1 ) \int \tan ^{2} x \mathrm{~d} x=\tan x-x+C\left(\tan ^{2} x=\sec ^{2} x-1\right) ∫tan2x dx=tanx−x+C(tan2x=sec2x−1) | |
| ∫ cot 2 x d x = − cot x − x + C ( cot 2 x = csc 2 x − 1 ) \int \cot ^{2} x \mathrm{~d} x=-\cot x-x+C\left(\cot ^{2} x=\csc ^{2} x-1\right) ∫cot2x dx=−cotx−x+C(cot2x=csc2x−1) |
凑微分法

例题
换元法
∫ f ( x ) d x = x = g ( u ) ∫ f [ g ( u ) ] d [ g ( u ) ] = ∫ f [ g ( u ) ] g ′ ( u ) d u \int f(x) \mathrm{d} x \stackrel{x=g(u)}{=} \int f[g(u)] \mathrm{d}[g(u)]=\int f[g(u)] g^{\prime}(u) \mathrm{d} u ∫f(x)dx=x=g(u)∫f[g(u)]d[g(u)]=∫f[g(u)]g′(u)du
换元后容易积分,则换元成功
- x = g ( u ) x=g(u) x=g(u)必须是单调可导函数
- 最后再带回去
三角函数代换

例子
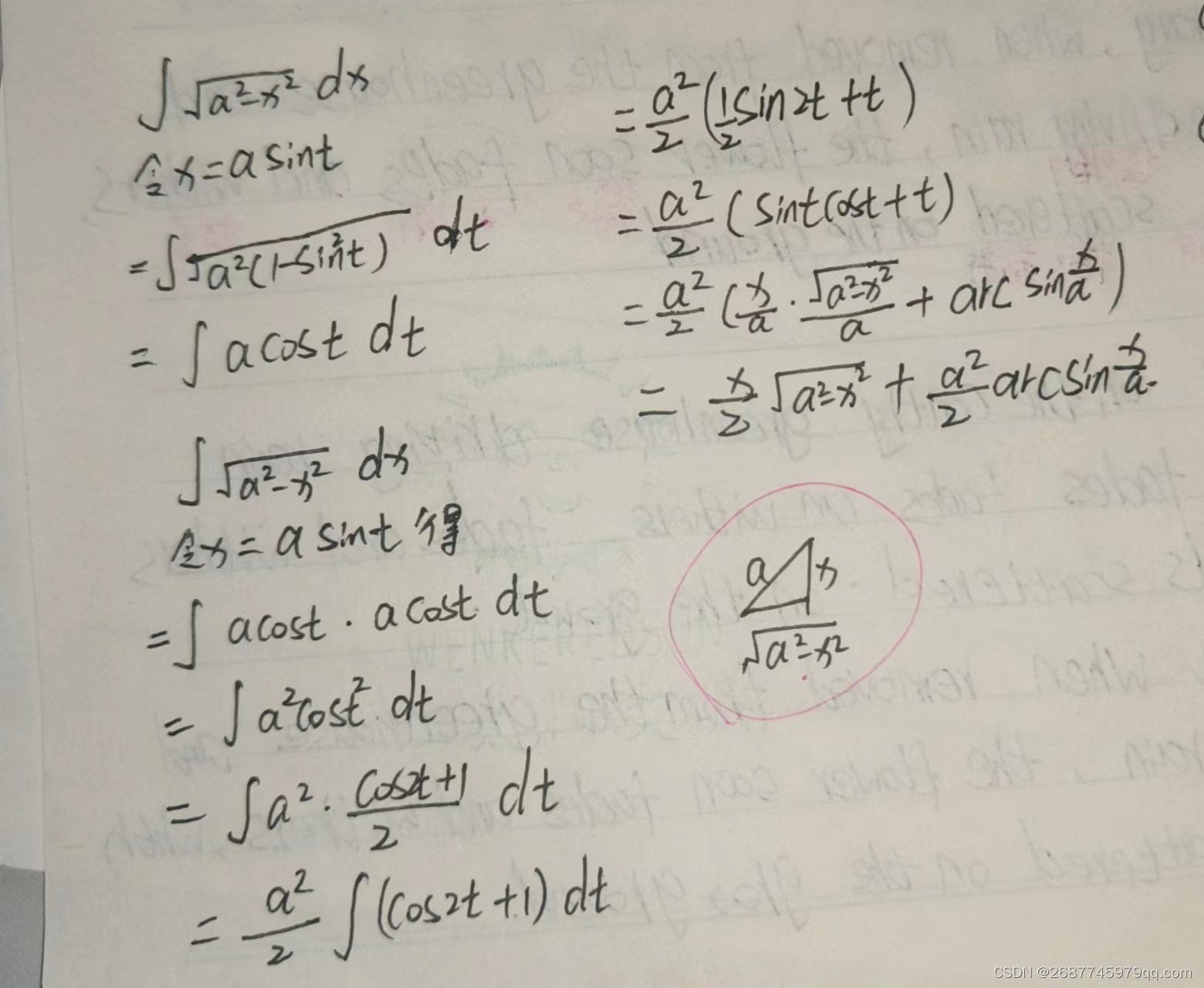
根式代换
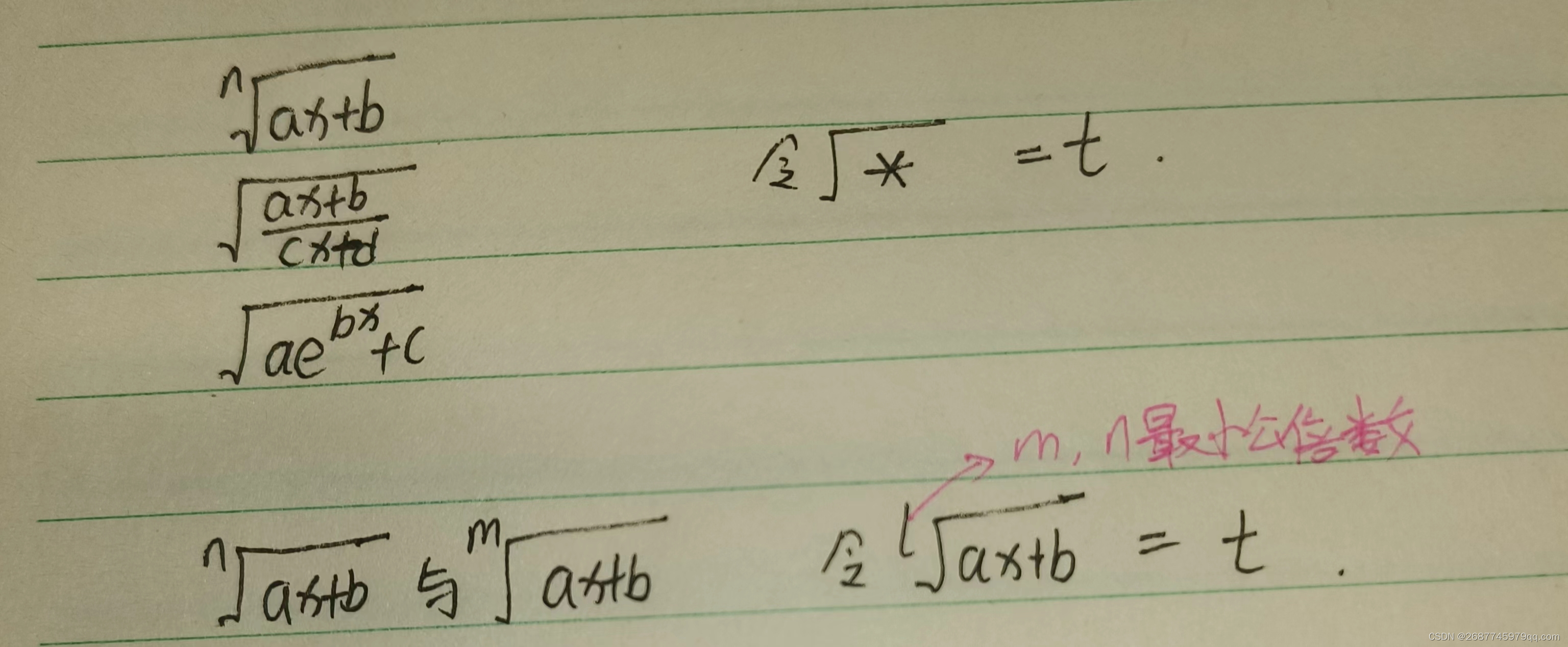
倒代换
分母比分子高两次幂
x = 1 t x=\frac{1}{t} x=t1
复杂函数
反三角、对数、幂函数、指数、三角函数与 P n ( x ) 或 e a x P_{n}(x) \text { 或 } \mathrm{e}^{a x} Pn(x) 或 eax相乘
反对幂指三与多项式或 e a x \mathrm{e}^{a x} eax相乘
使用分部积分法
其余使用直接代换
2 ∗ = t \sqrt{2} \sqrt{*}=t 2∗=t
分部积分法
∫ u d v = u v − ∫ v d u {\Large \int u \mathrm{~d} v=uv-\int v \mathrm{~d} u} ∫u dv=uv−∫v du
u u u通常为容易求导的

Pro版
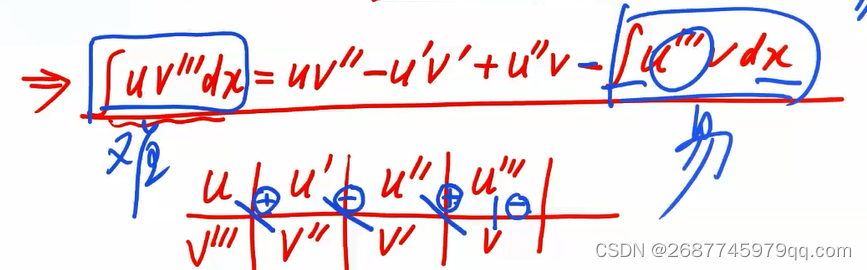
有理函数积分法
形如
∫
P
n
(
x
)
Q
m
(
x
)
d
x
(
n
<
m
)
的积分称为有理函数的积分
\text { 形如 } \int \frac{P_{n}(x)}{Q_{m}(x)} \mathrm{d} x(n<m) \text { 的积分称为有理函数的积分 }
形如 ∫Qm(x)Pn(x)dx(n<m) 的积分称为有理函数的积分 ,分母必须在实数域内
先因式分解,再拆分
- 分母的一次单因式 a x + b 产生一项 A a x + b ; \text { 分母的一次单因式 } a x+b \text { 产生一项 } \frac{A}{a x+b} \text {; } 分母的一次单因式 ax+b 产生一项 ax+bA;
- 分母的 k 重一次因式 ( a x + b ) k 产生 k 项 A 1 a x + b + A 2 ( a x + b ) 2 + ⋯ + A k ( a x + b ) k \text{ 分母的} k \text { 重一次因式 }(a x+b)^{k} \text { 产生 } k \text { 项 } \frac{A_{1}}{a x+b}+\frac{A_{2}}{(a x+b)^{2}}+\cdots+\frac{A_{k}}{(a x+b)^{k}} 分母的k 重一次因式 (ax+b)k 产生 k 项 ax+bA1+(ax+b)2A2+⋯+(ax+b)kAk
- 分母的二次单因式 p x 2 + q x + r 产生一项 A x + B p x 2 + q x + r \text { 分母的二次单因式 } p x^{2}+q x+r \text { 产生一项 } \frac{A x+B}{p x^{2}+q x+r} 分母的二次单因式 px2+qx+r 产生一项 px2+qx+rAx+B
- 分母的 k 重二次因式 ( p x 2 + q x + r ) k 产生 k 项 A 1 x + B 1 p x 2 + q x + r + A 2 x + B 2 ( p x 2 + q x + r ) 2 + ⋯ + A k x + B k ( p x 2 + q x + r ) k \text{分母的} k \text{重二次因式} \left(p x^{2}+q x+r\right)^{k} 产生 k 项\frac{A_{1} x+B_{1}}{p x^{2}+q x+r}+\frac{A_{2} x+B_{2}}{\left(p x^{2}+q x+r\right)^{2}}+\cdots+\frac{A_{k} x+B_{k}}{\left(p x^{2}+q x+r\right)^{k}} 分母的k重二次因式(px2+qx+r)k产生k项px2+qx+rA1x+B1+(px2+qx+r)2A2x+B2+⋯+(px2+qx+r)kAkx+Bk
例题
求参数时优先特殊值代入

定积分计算
牛莱公式
一般适用于连续函数
∫
a
b
f
(
x
)
d
x
=
F
′
(
x
)
=
f
(
x
)
F
(
x
)
∣
a
b
=
F
(
b
)
−
F
(
a
)
\left.\int_{a}^{b} f(x) \mathrm{d} x \stackrel{F^{\prime}(x)=f(x)}{=} F(x)\right|_{a} ^{b}=F(b)-F(a)
∫abf(x)dx=F′(x)=f(x)F(x)
ab=F(b)−F(a)
对于振荡间断点也适用
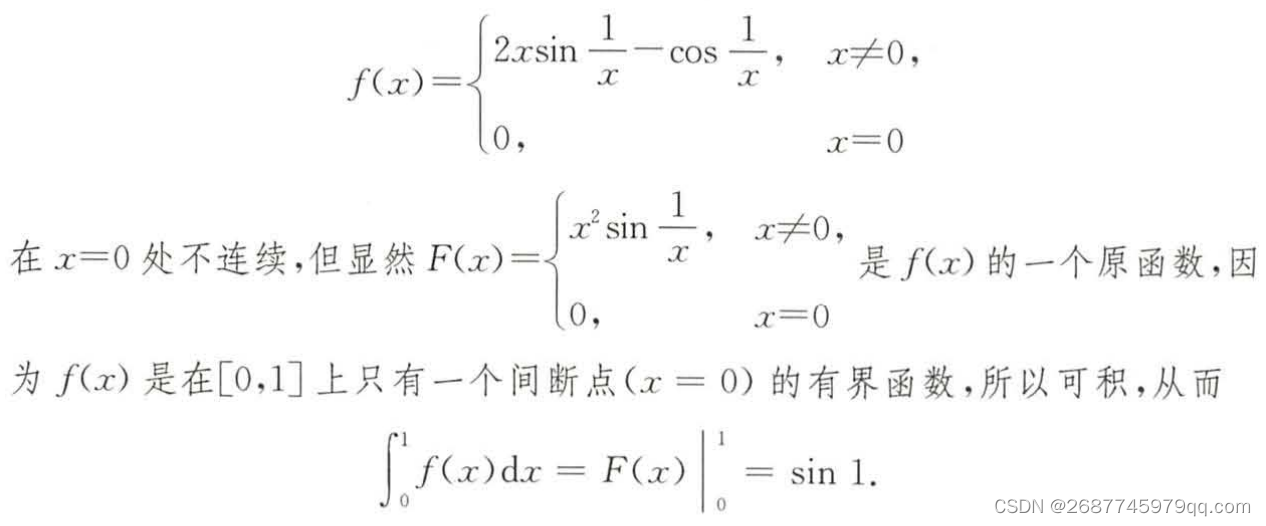
变限积分计算
换元法
要三换
被积函数,积分变量,上下限

分部积分法
∫
a
b
u
v
′
d
x
=
u
v
∣
a
b
−
∫
a
b
v
u
′
d
x
{\large \int_{a}^{b} u v^{\prime} \mathrm{d} x=\left.u v\right|_{a} ^{b}-\int_{a}^{b} v u^{\prime} \mathrm{d} x}
∫abuv′dx=uv∣ab−∫abvu′dx
找易求导

反常积分计算
在收敛条件下,反常积分与定积分通过换元有可能实现转换
微积分考点解析



偶倍奇零

区间再现公式
∫ a b f ( x ) d x = ∫ a b f ( a + b − x ) d x \int_{a}^{b} f(x) \mathrm{d} x=\int_{a}^{b} f(a+b-x) \mathrm{d} x ∫abf(x)dx=∫abf(a+b−x)dx
证明
令 x = a + b − t x=a+b-t x=a+b−t代入即可
使用

华里士公式
证明
由分部积分法求出的递推公式可证

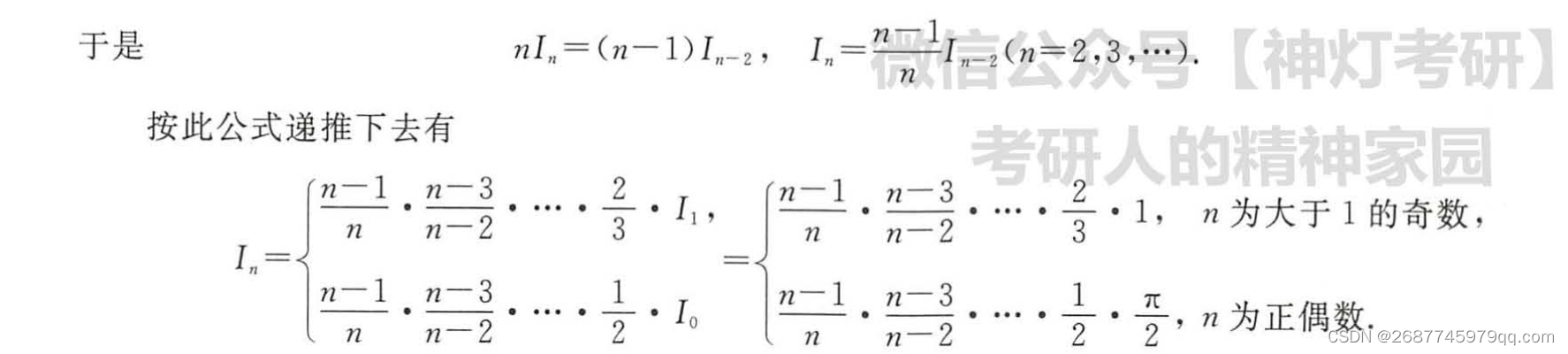





















 4782
4782











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








