1、Nerf体渲染
1.1 原理
 其次就重点了解神经体渲染了:
其次就重点了解神经体渲染了:
之前我一直把体渲染和新视角合成搞混了,我理解体渲染就是新视角合成,但并不是这样,体渲染是新视角合成的一个工具。
体积渲染技术的原理是:相机沿着特定方向进行观测,等价于从相机位置沿着这个方向发射出去一条光线,光线路径上的点是连续分布的,相机成像平面上该方向对应的像素颜色,可以计算为光线经过的点的颜色积分。
体渲染是指对已知视角的图片发出的某条光线进行均匀采样,然后计算这些采样点的密度和颜色,然后利用体积渲染公式对这条光线上所有采样点的颜色和密度进行积分得到发出这条光线的原始图像上像素的颜色,并且由于是已知视角的图像,我们有本来这个像素的颜色,因此体渲染利用真实的像素颜色和渲染得到的像素颜色计算损失值来不断的优化每个采样点的密度和颜色。那么一个数据集有多张图片,一张图片上有多个像素,每个像素发出一条光线,每条光线上都有多个采样点,并且通过计算渲染图像和真实图像间的颜色损失来优化采样点的密度和颜色,最后就使得我们计算得到的3D场景中采样点的颜色和密度都很逼真,那么同样可以利用体渲染技术将这些已知的采样点沿未知视角的光线来合成未知视角的图片了,这就是新视角合成。
并且体渲染是三维数据到2D图像,而新视角合成是利用已知的2D图像合成未知的2D图像。
1.2 公式
下述是体渲染公式:
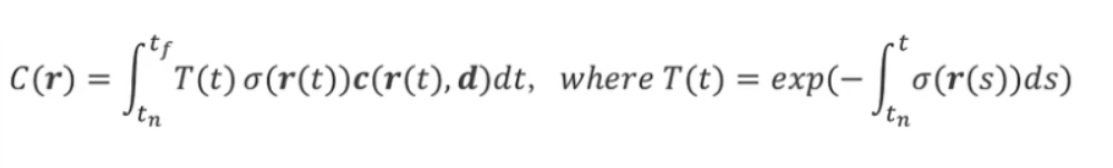
其中C代表的是颜色;r(t)=o+td代表的是视线,o是光心,t是光心到采样点的距离,d是相机观测方向;积分代表对视线上的所有采样点的相关值(密度、颜色、透明率三者的乘积)进行累加;tn和tf代表采样的范围;σ(r(t))是采样点的密度,密度值σ只与采样点的坐标有关;c(r(t),d)代表采样点的颜色,颜色值c与视线方向和采样点的坐标都有关系;T(t)为累计透射率(透明率),其公式如上图,有一个积分值,积分值就代表光心点(起始点)到当前采样点的每个点密度值的累积和,T(t)的最终值就等于这个积分值的负数作为e的指数。
对于T(t)更加细致的理解:σ(r(t))也代表采样点位置物理材质吸收光线的能力,当σ=0时,代表不吸收光线,就像空气一样光线一下就投射过去了,不参与颜色的计算;当σ=+∞时,代表不透光,也就是说这个位置把光线都吸收完了,光线穿透不过去,不参与颜色的运算;当σ位于0与+∞之间时,代表这个位置吸收一部分光线,其余的光线可以透射过去,参与颜色的运算。那么只要一个采样点吸收了光线,那么它的颜色就是看得到的。但是光线一旦从摄像机光心发出,那么它就在衰减,后面可能会衰减至0,衰减至0之后即使后面有存在σ的物体(采样范围之内)也会因为没有吸收到光线而不被渲染出来,那么光线的衰减程度就是利用T(t)透射率来表示的,也可以将其理解为光强,其值为0~1,在空气中其值为1,穿过物体之后就慢慢衰减。可以看出T(t)是与吸光材质有关的,因此T(t)的值里面有密度值的积分,但是我们又希望T(t)的范围为0~1,所以就给积分值加上一个负号之后作为e的指数,可以看出光线在空气中时,T(t)=1,当光线穿过物体之后,T(t)的值也会慢慢衰减为0。
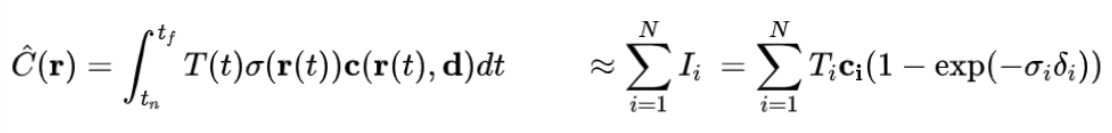
起初体渲染公式是积分,但是积分是针对于连续空间,而我们的采样点是离散的,所以需要整理为上图的求和的公式。具体怎么做看后面的分析:
 那么可以得到:
那么可以得到:
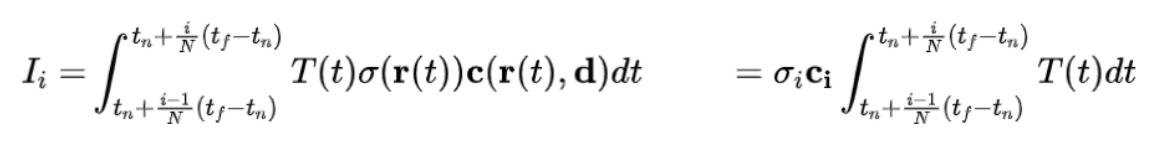
又由于T(t)是从光线起点处开始积分计算,所以T(t)可以拆分为两段的乘积:

那么:
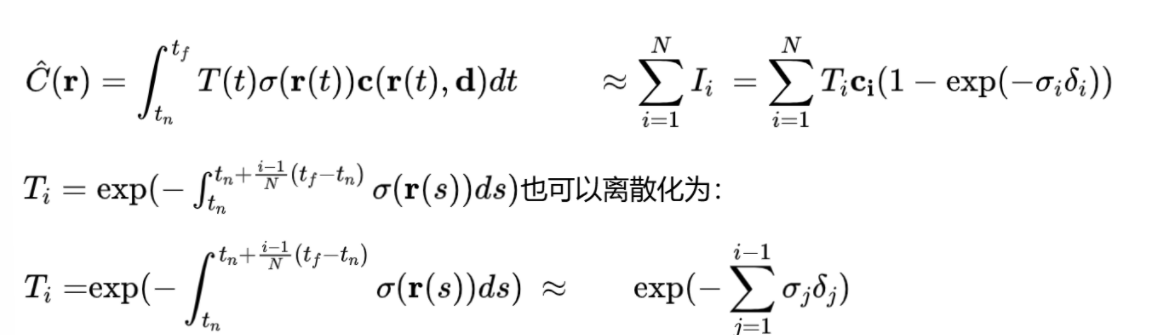
1.3 代码
在NeRF(Neural Radiance Fields)的GitHub代码库中,run_nerf.py:包含体积渲染的核心函数,实现了光线投射和累积颜色密度的计算。render_rays 函数是实现体渲染公式的核心,其中最重要的部分是 raw2outputs 函数。以下是这些代码的详细解析:
def render_rays(ray_batch, network_fn, network_query_fn, N_samples, retraw=False, lindisp=False, perturb=0., N_importance=0, network_fine=None, white_bkgd=False, raw_noise_std=0., verbose=False):
...
def raw2outputs(raw, z_vals, rays_d):
...
def raw2alpha(raw, dists, act_fn=tf.nn.relu):
return 1.0 - tf.exp(-act_fn(raw) * dists)
#距离计算
#相邻采样点之间的距离
dists = z_vals[..., 1:] - z_vals[..., :-1]
#在距离数组的末尾添加一个大值,这是为了处理边界情况,即在光线的最后一个采样点后没有下一个采样点,因此距离设置为一个非常大的值。
dists = tf.concat([dists, tf.broadcast_to([1e10], dists[..., :1].shape)], axis=-1)
#将距离转换为实际距离,其中rays_d是光线方向
dists = dists * tf.linalg.norm(rays_d[..., None, :], axis=-1)
#颜色计算,raw[..., :3] 是模型的输出值,表示光线在每个采样点的原始颜色值。通过 Sigmoid 函数将这些原始值转换为在 0 到 1 范围内的实际颜色值。
rgb = tf.math.sigmoid(raw[..., :3])
#噪声添加,体渲染过程中向密度值添加噪声,以防止模型过拟合并提高模型的鲁棒性
noise = 0.
if raw_noise_std > 0.:
noise = tf.random.normal(raw[..., 3].shape) * raw_noise_std
#透射率α的计算,调用 raw2alpha 函数,将网络的密度预测值raw[..., 3]和距离dists输入进去,得到透射率,就相当于密度值。
alpha = raw2alpha(raw[..., 3] + noise, dists)
#tf.math.cumprod(1.-alpha + 1e-10, axis=-1, exclusive=True)为T的计算
weights = alpha * tf.math.cumprod(1.-alpha + 1e-10, axis=-1, exclusive=True)
#最终颜色和深度计算
rgb_map = tf.reduce_sum(weights[..., None] * rgb, axis=-2)
depth_map = tf.reduce_sum(weights * z_vals, axis=-1)
disp_map = 1./tf.maximum(1e-10, depth_map / tf.reduce_sum(weights, axis=-1))
acc_map = tf.reduce_sum(weights, -1)
if white_bkgd:
rgb_map = rgb_map + (1.-acc_map[..., None])
return rgb_map, disp_map, acc_map, weights, depth_map
N_rays = ray_batch.shape[0]
#光线起点和方向
rays_o, rays_d = ray_batch[:, 0:3], ray_batch[:, 3:6]
viewdirs = ray_batch[:, -3:] if ray_batch.shape[-1] > 8 else None
bounds = tf.reshape(ray_batch[..., 6:8], [-1, 1, 2])
near, far = bounds[..., 0], bounds[..., 1]
#采样点的生成
t_vals = tf.linspace(0., 1., N_samples)
if not lindisp:
z_vals = near * (1.-t_vals) + far * t_vals
else:
z_vals = 1./(1./near * (1.-t_vals) + 1./far * t_vals)
z_vals = tf.broadcast_to(z_vals, [N_rays, N_samples])
#扰动采样点,生成扰动后的采样点,避免过拟合并增加模型的鲁棒性。
if perturb > 0.:
mids = .5 * (z_vals[..., 1:] + z_vals[..., :-1])
upper = tf.concat([mids, z_vals[..., -1:]], -1)
lower = tf.concat([z_vals[..., :1], mids], -1)
t_rand = tf.random.uniform(z_vals.shape)
z_vals = lower + (upper - lower) * t_rand
#计算采样点坐标
pts = rays_o[..., None, :] + rays_d[..., None, :] * z_vals[..., :, None]
#查询网络获取原始输出,也就是密度值
raw = network_query_fn(pts, viewdirs, network_fn)
rgb_map, disp_map, acc_map, weights, depth_map = raw2outputs(raw, z_vals, rays_d)
...
2、Neus提取网格原理
2.1 原理
Neus的网格提取主要是根据Marching Cubes 算法实现。NeuS 利用体积渲染生成密度场。通过对密度场进行采样,使用 Marching Cubes 算法提取网格表面。
密度场是一个在三维空间中定义的标量场,其中每个点的值表示该位置的密度。通过Nerf的体渲染技术得以实现。
三线性插值
简单来说,插值指的是通过对端点的平均来得到一个函数的中间点值的过程。
三线性插值是双线性插值向三维空间的推广,对于三线性插值,给定八个点
![]()
,其中ijk在0-1之间。我们的目标是定义一个从单位立方体到三维空间的光滑映射,其八个点大概在长方体的顶点位置上,而函数u(α,β,γ)应该是一个光滑的插值函数:
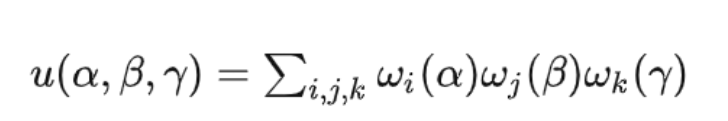
其中的求和针对所有的i,j,k区间在0-1,而其值
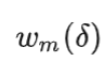
(n是在区间0-1)定义如下:

三线性插值也可以对函数进行插值,假设函数f指定了在顶点上的值,因此,
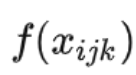
在所有的八个顶点上为固定值,然后使用三线性插值将f扩展到单位立方体上:
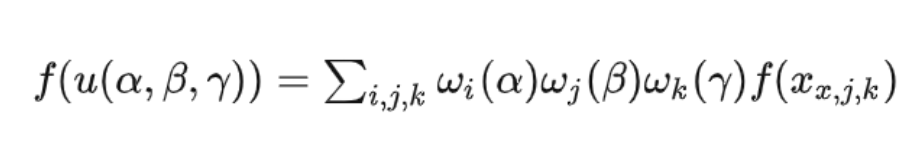
Marching cubes(行进的立方体)是一种简单的迭代算法。它用来为3D函数(体素)计算三角形平面。
Marching cubes通过在已划分为多个小立方体的3D区域Marching(行进)进行工作。每个小立方体都有8个顶点,每个顶点都看为一个体素,如果这个顶点位于3D物体表面内,那么其对应的体素值为0,如果这个顶点位于3D物体表面外,那么其对应的体素值为1。那么Marching cubes算法的基本思想就是根据每个小立方体各个顶点的体素值,计算这个立方体的三角形平面,进而用这个三角形平面表示我们3D物体的表面,但是如果一个立方体8个顶点的体素值都为1,也就是完全位于物体外,那么这个立方体是没有三角平面的,因为根本没有经过物体,同样如果8个体素值都为0,也就是完全位于物体内,那么这个立方体也是没有三角平面的,因此Marching cubes算法的目的是计算一些点位于物体表面外,其余点在物体表面内的立方体的三角平面。由于一个立方体8个顶点,每个顶点的值有两种可能:0和1,那么每个立方体的体素配置有28=256个。
那么我们知道一个3D区域是很大的,将它可划分为很多个立方体,而每个立方体有256个配置,那么计算量太大,因此Marching cubes算法的巧妙之处就是使用以下两种方法来处理256个配置:
-
将256个配置减少为16个(考虑了旋转和镜像对称引起的冗余)。
-
使用一个聪明的索引表,加快了查找的速度。
由于立方体不好描述,这里采用二维平面(对应立方体每个面的正方形)的方式来对 Marching cubes进一步进行说明。下图是将3D空间划分为无数个立方体,二维平面表示为无数个正方形。
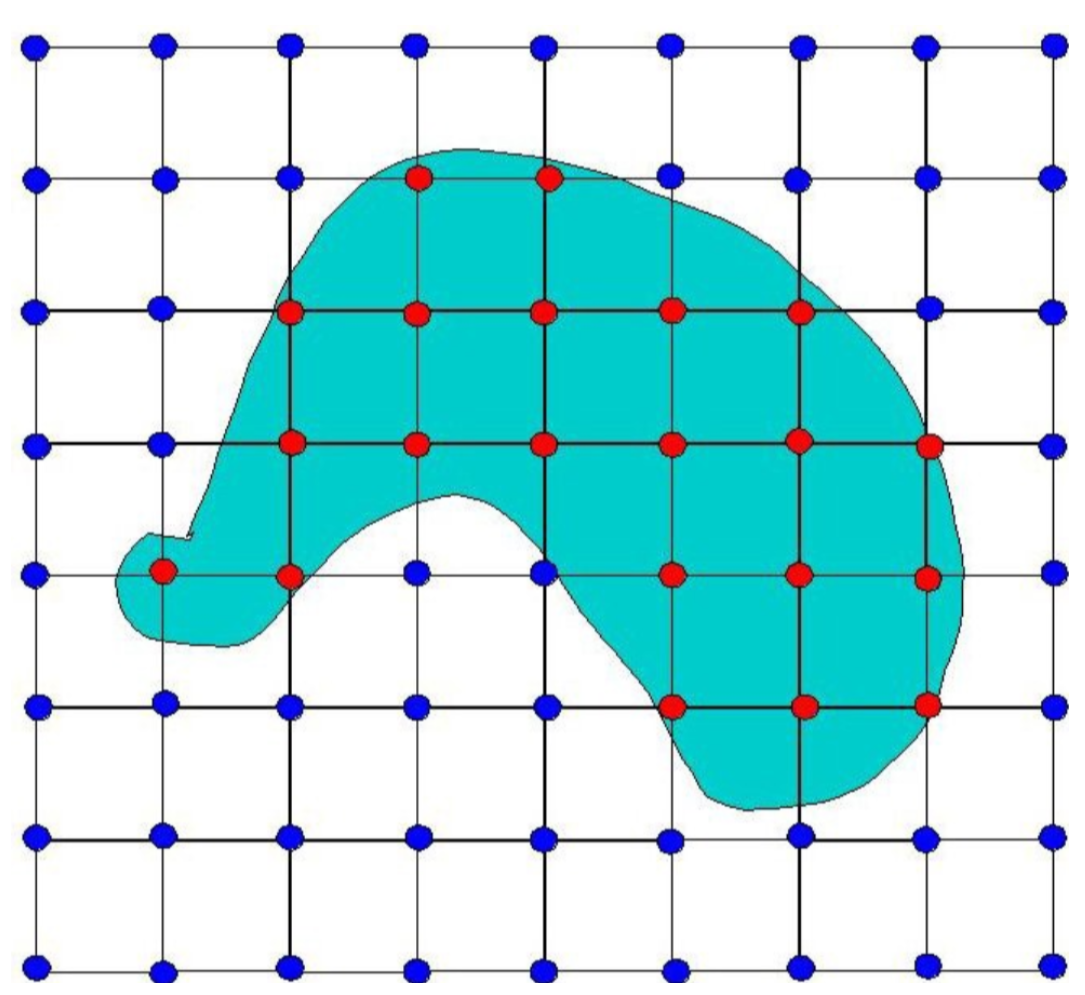
上图中的蓝色部分是我们的3D物体,其中蓝色的点代表位于物体外的点,红色的点代表位于物体内的点。现在可以看到正方形(3D的立方体)的配置,全部为蓝色边角点的正方形不用计算三角形平面,全部为红色边角点的正方形也不用计算三角形平面,使用Marching cubes算法计算有红有蓝正方形的正方形配置,也就是3D物体边界是如何穿过正方形的。
由于一个正方形有4个点,那么有24=16种配置,如下:
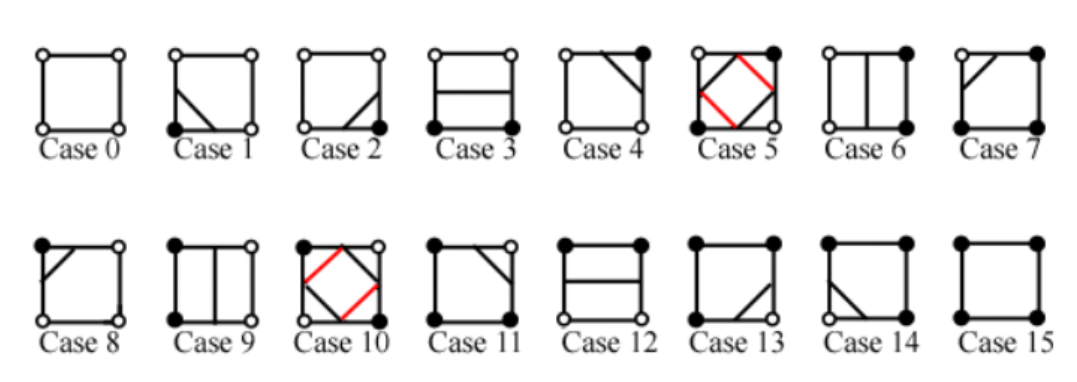
根据这种配置在图像上进行标点,如下:
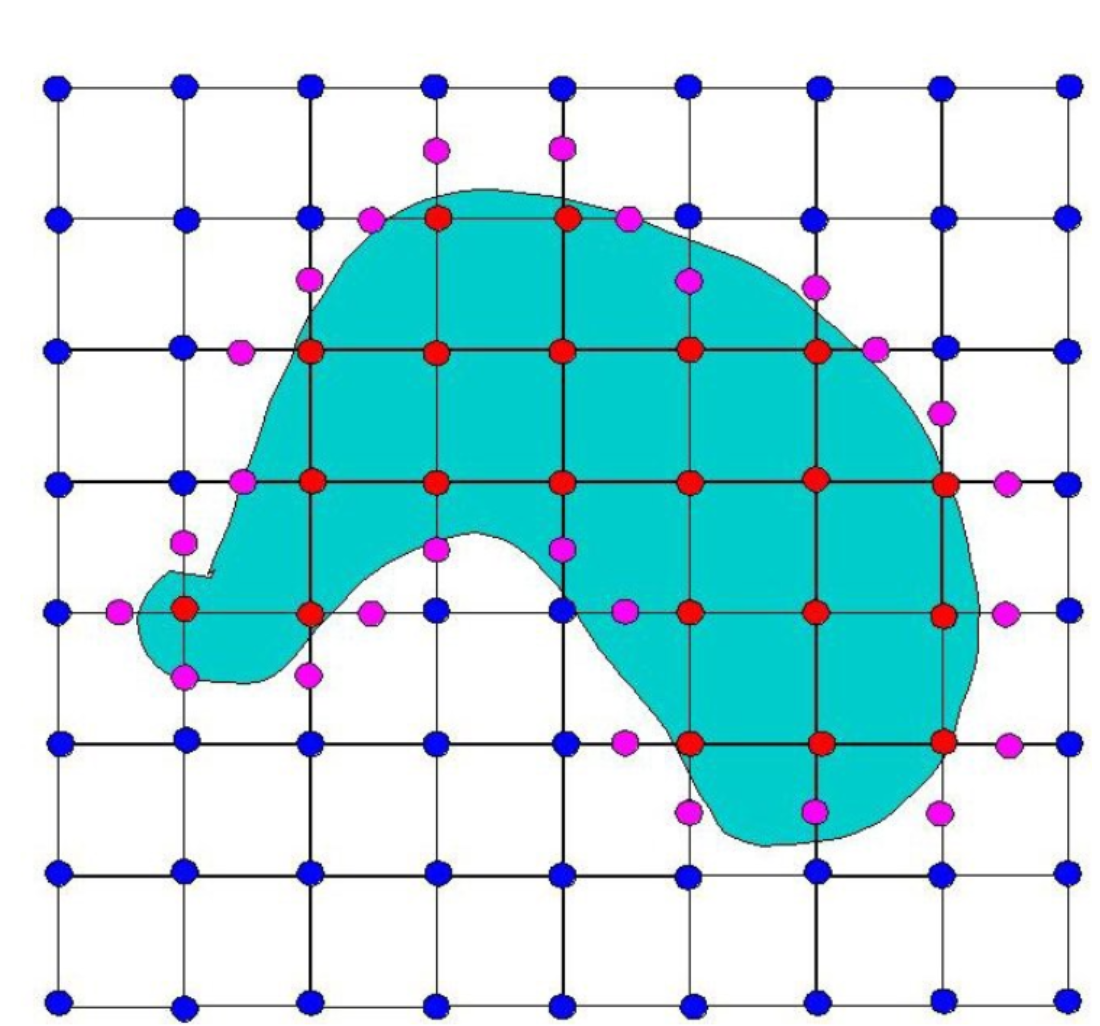
将标记的粉红色的点进行连线,就可以表示出整个物体边界在二维平面上的映射,如下:
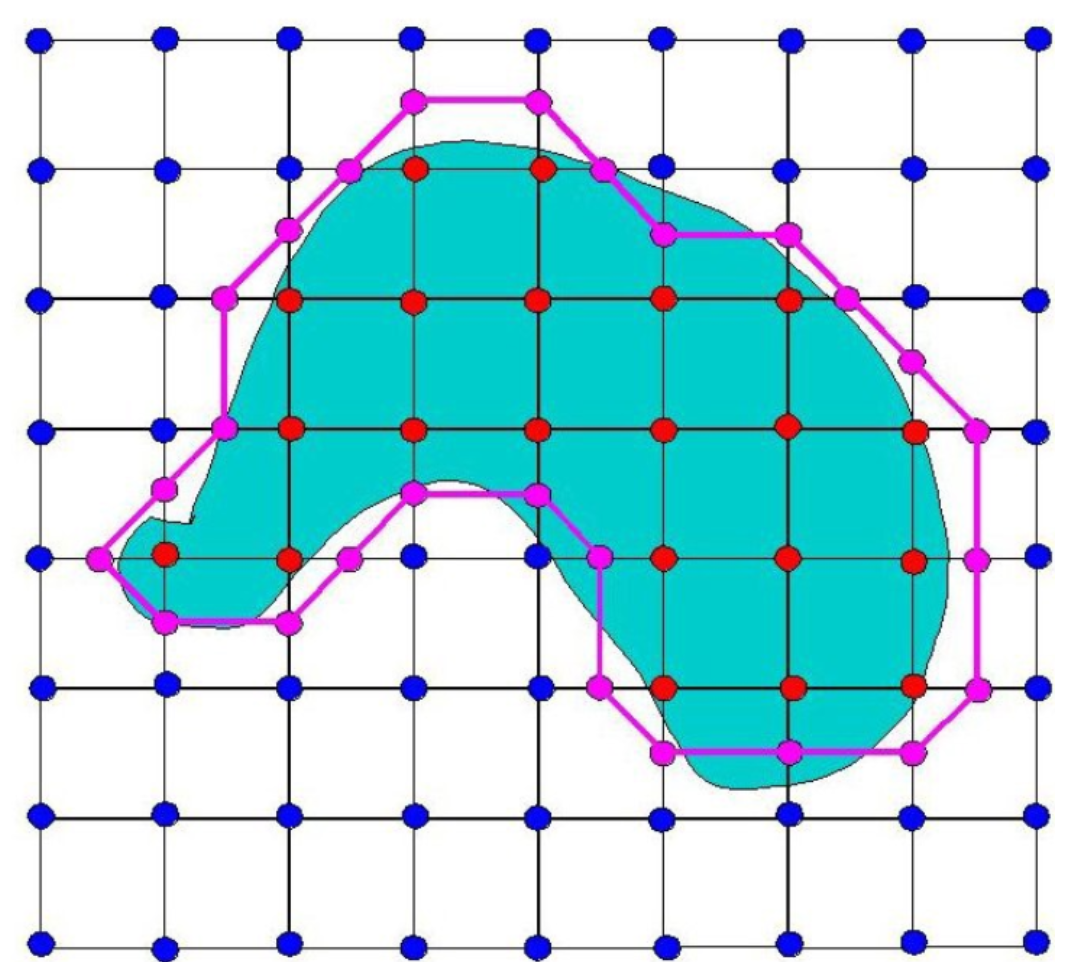
可以看出来效果不是很好,所以可以采样以下两种方法进行改进:
-
将立方体划分得更小。
-
采用比较好的插值策略
以上两种方法都会对最终的效果起到改进作用,但是第一种方法由于立方体的个数增加了,那么Marching cubes算法计算的配置数量一定增加,就会耗费大量的时间成本。那么另一个方法是比较好的因为可以看到刚刚标记的粉红色的点都是每条边的一个中点,这样的物体边界一定粗糙,那么就可以选用一个比较好的插值方法,利用均值的方法得到一个较为合适的点,使得最后得到的边界可以更加精确。
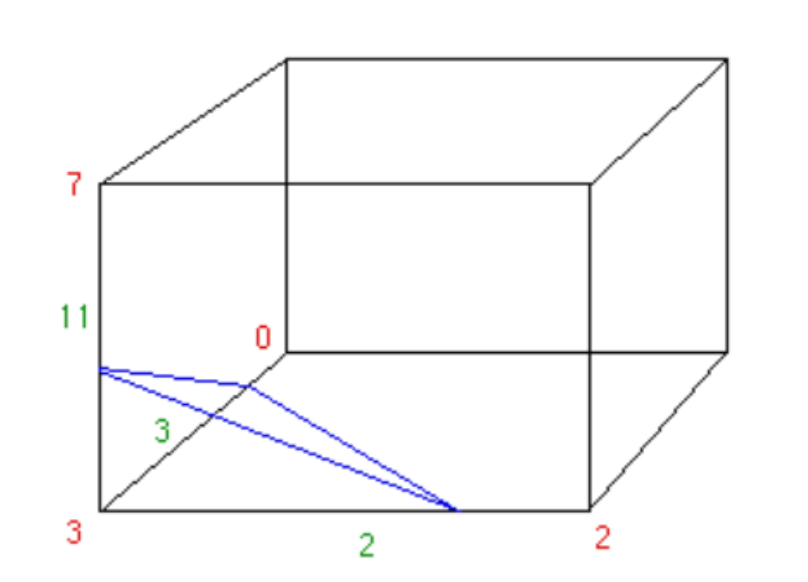
上图是Marching cubes算法计算的一个立方体的三角平面,也就是说物体在三维空间中就是以这样的方式穿过这个立方体的。
密度场和Marching cubes的结合:在 NeuS 中,通过神经网络生成密度场,然后使用 Marching Cubes 算法从密度场中提取网格顶点和三角面片,实现隐式表面的重建。以下是 Marching Cubes 的具体工作流程:
-
输入密度场:神经网络预测的三维密度场。
-
划分立方体:将整个密度场划分为许多小立方体。
-
判断顶点状态:对于每个立方体,判断其顶点密度值是位于等值面内还是等值面外。(这里不是体素值了,而是密度值)
-
生成等值面:根据立方体顶点的状态,使用查找表生成等值面的三角形片。
-
组合网格:将所有立方体生成的三角形片组合成完整的网格。
2.2 代码
在 NeuS GitHub 仓库中,提取网格的代码主要在 exp_runner.py 中的 validate_mesh 模式下运行,提取网格的关键代码在 validate_mesh 函数中。
def validate_mesh(self, world_space=False, resolution=64, threshold=0.0):
#这两行代码获取物体边界框的最小和最大值,用于定义提取网格的空间范围。
bound_min = torch.tensor(self.dataset.object_bbox_min, dtype=torch.float32)
bound_max = torch.tensor(self.dataset.object_bbox_max, dtype=torch.float32)
#通过调用 extract_geometry 函数,使用 Marching Cubes 算法从密度场中提取网格顶点和三角面片。
vertices, triangles =\
self.renderer.extract_geometry(bound_min, bound_max, resolution=resolution, threshold=threshold)
#创建存储网格文件的目录。
os.makedirs(os.path.join(self.base_exp_dir, 'meshes'), exist_ok=True)
#如果需要将网格转换为世界坐标系,应用缩放和偏移矩阵。
if world_space:
vertices = vertices * self.dataset.scale_mats_np[0][0, 0] + self.dataset.scale_mats_np[0][:3, 3][None]
#使用 trimesh 库创建网格对象,并将其导出为 PLY 文件。
mesh = trimesh.Trimesh(vertices, triangles)
mesh.export(os.path.join(self.base_exp_dir, 'meshes', '{:0>8d}.ply'.format(self.iter_step)))
logging.info('End')























 672
672

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








