🐺本博主博客:ζั͡ ั͡雾 ั͡狼 ั͡✾的博客
🎀专栏:机器学习
🎀专栏:爬虫
🎀专栏:OpenCV图像识别处理
🎀专栏:Unity2D
⭐本节课理论视频: :P33-P38逻辑回归
⭐本节课推荐笔记:吴恩达逻辑回归总结_蓝色的紫的博客
🐺机器学习通过文字描述是难以教学学会的,每一节课我会推荐这个理论的网课,一定要看上面的理论视频!一定要看上面的理论视频!一定要看上面的理论视频!所以我只是通过代码实现,并通过注释形式来详细讲述每一步的原因,最后通过画图对比的新式来看结果比较。
⭐机器学习推荐博主:GoAI的博客_CSDN博客-深度学习,机器学习,大数据笔记领域博主
😊如果你什么都不懂机器学习,那我推荐GoAI的入门文章:机器学习知识点全面总结_GoAI的博客-CSDN博客_机器学习笔记
非线性逻辑回归,主要通过给出的俩个变量,构建出一个新的矩阵,这个矩阵的其他元代表给出的这俩个变量的高次数。再根据上一节课的步骤做出来就行。主要需要注意最后得到的K系数矩阵对应的变量的次方。这个代码我也没写的太好,到更高次通用性不好,但由于写出一个通用性代码太费时间了,就直接拿二次函数和三次函数举例就行,如果你感兴趣,你可以根据规律,构建一个有规律的矩阵,并规律的给它乘上相应的回归得到的系数k,构建出我们最后的决策界限和假设函数
(1)二次函数回归分界线
import numpy as np
import matplotlib.pyplot as plt
# 全局变量
# 生成数据
#X每一行代表了x1,x2的值,并且相应对应下面y的分类
X =np.array([[0,1],
[1,1],
[1,0],
[1,2],
[2,1],
[3,0],
[0,3],
[2,2],
[2,3]])
# Y中的数据量等于X矩阵的行数,二分类,Y只能取0,1
Y = np.array([0,0,0,1,1,0,0,0,1])
#构造模拟的曲线次方
power=2
#获取变量默认为俩个变量
for i in range(power+1):
for j in range(power+1):
#通过俩个变量x1,x2构建高次函数
if(i+j<=power&i+j>1):
newX=np.power(X[:,0],i)*np.power(X[:,1],j)
print("x1次方",i,"x2次方",j)
X=np.append(X,np.array([newX]).T,axis=1)
# 开始
# 学习率,在代价函数斜率线上移动的距离步子大小
A = 0.1
# 迭代次数
time = 100000
# 进行归一化操作
# 获取每列平均值
u = np.average(X, axis=0)
# 获取没列的标准差
s = np.std(X, axis=0)
# 按行复制,构成X同形状矩阵
U = np.repeat([u], len(X), axis=0)
S = np.repeat([s], len(X), axis=0)
# 归一化,注意归一化所求的系数矩阵K是(X-U)/S的系数,真正系数,需要将x参数前面的系数合并
X= (X - U) / S
# X矩阵中第一列加入x0=1参数,便于构建常数项
X = np.insert(X, 0, np.ones((1, len(X))), axis=1)
# 数据个数
m = len(X)
# 参数个数
n = len(X[0])
# 系数变量K矩阵就是多元参数的系数,就是我们要递归的重点变量,先给这个矩阵的每个值都赋予初始值1
K = np.ones(n)
# 输出
print(f"有{n}个参数,就是X列数+常数项所乘的单位1")
print(f"有{m}条数据,就是加常数后X行数")
# 假设函数
# 在逻辑回归中我们设定的假设函数是H=1/(1+e^(-KX))这个值在0-1之间,可以当作概率
def H(Xi):
global K
y=np.dot(K, Xi.T)
if y>0:
return 1/(1+np.power(np.e,-y)) # xi需要转置,才能得到内积和
else:#为负数的时候,对sigmoid函数的优化,避免了出现极大的数据溢出
return np.power(np.e, y) / (1 + np.power(np.e, y))
# 代价函数L=求和((H(x)-y(x))^2),其中H是关于K矩阵中所有系数参数的函数
# 代价函数就是你估算的值与实际值的差的大小,使得代价函数最小,这样就能不断逼近结果
# 使得代价函数最小,就要使得初始点在斜率线上不断往低处移动,呈现出系数的不断微小移动
# 固定公式格式,推导原理看吴恩达P11
def dL_K(): # 代价函数对矩阵中系数参数k求导
global X, Y, K, m, n
dL_Karr = np.empty(n) # 数组用来存放L对每个k求导后的结果
for j in range(n):
ans = 0
for i in range(m):
ans += ((H(X[i]) - Y[i]) * X[i][j]) # 由于k的系数是x,所以求导后还要乘x
dL_Karr[j] = ans
return dL_Karr
def itreation(time): # 迭代,使O1,O2的代价函数趋于最低点
global K
for i in range(time):
# 一次迭代过程中代价函数对系数k的导数数组
dL_Karr = dL_K()
# 同时变化,减法原因是正斜率使得O更小,负斜率使得O更大,不断往低处移动即代价函数最小
K = K - A * dL_Karr
if (i % 10000 == 0): # 每100次输出一次
print(f"迭代了{i}次,变量的系数矩阵K为{K}")
if __name__ == "__main__":
print("X",X)
print("Y",Y)
itreation(time)
print('归一化系数(第一个是常数)', K, )
# 注意归一化所求的系数矩阵K是(X-U)/S的系数,真正系数,需要将x参数前面的系数合并
#计算真正的X
X[:,1:]=(X[:,1:]+U)*S
# 忽略前一位常数,计算真正系数
K[1:] = K[1:] / s
# 利用真正系数,计算真正常数
K[0] = K[0] - np.sum(K[1:] * u)
print('真正系数矩阵', K)
#绘图,注意x轴是确定参数x1,y轴是确定参数x2
x1=X[:, 1]
x2=X[:, 2]
#画出决策界线,分界线是x2作为y轴,x1作为x轴,KX=0的线
#构造网络
x=np.linspace(-1,5,1000)
y = np.linspace(-1, 5, 1000)
x,y=np.meshgrid(x,y)
z=K[0]+K[1]*x+K[2]*y+K[3]*y*y+K[4]*x*y+K[5]*x*x
plt.contour(x,y,z,0)
plt.scatter(x1[Y==0], x2[Y==0],c='r',marker='x')
plt.scatter(x1[Y==1], x2[Y==1],c='g',marker='o')
plt.xlabel("x1")
plt.ylabel("x2")
plt.show()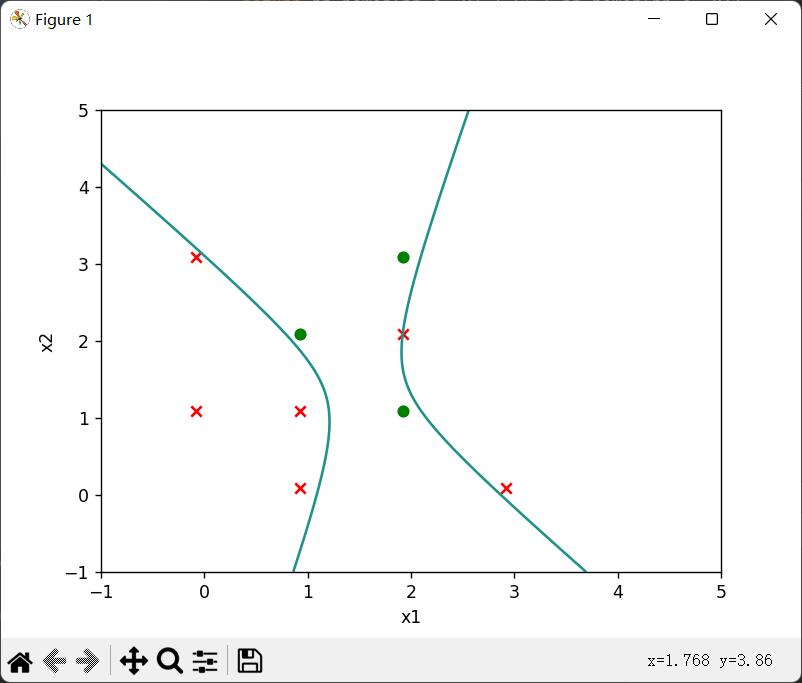
(2)三次函数回归分界线
import numpy as np
import matplotlib.pyplot as plt
# 全局变量
# 生成数据
#X每一行代表了x1,x2的值,并且相应对应下面y的分类
X =np.array([[0,1],
[1,1],
[1,0],
[1,2],
[2,1],
[3,0],
[0,3],
[2,2],
[2,3]])
# Y中的数据量等于X矩阵的行数,二分类,Y只能取0,1
Y = np.array([0,0,0,1,1,0,0,0,1])
#构造模拟的曲线次方
power=3
#获取变量默认为俩个变量
for i in range(power+1):
for j in range(power+1):
#通过俩个变量x1,x2构建高次函数
if(i+j<=power&i+j>1):
newX=np.power(X[:,0],i)*np.power(X[:,1],j)
print("x1次方",i,"x2次方",j)
X=np.append(X,np.array([newX]).T,axis=1)
# 开始
# 学习率,在代价函数斜率线上移动的距离步子大小
A = 0.1
# 迭代次数
time = 100000
# 进行归一化操作
# 获取每列平均值
u = np.average(X, axis=0)
# 获取没列的标准差
s = np.std(X, axis=0)
# 按行复制,构成X同形状矩阵
U = np.repeat([u], len(X), axis=0)
S = np.repeat([s], len(X), axis=0)
# 归一化,注意归一化所求的系数矩阵K是(X-U)/S的系数,真正系数,需要将x参数前面的系数合并
X= (X - U) / S
# X矩阵中第一列加入x0=1参数,便于构建常数项
X = np.insert(X, 0, np.ones((1, len(X))), axis=1)
# 数据个数
m = len(X)
# 参数个数
n = len(X[0])
# 系数变量K矩阵就是多元参数的系数,就是我们要递归的重点变量,先给这个矩阵的每个值都赋予初始值1
K = np.ones(n)
# 输出
print(f"有{n}个参数,就是X列数+常数项所乘的单位1")
print(f"有{m}条数据,就是加常数后X行数")
# 假设函数
# 在逻辑回归中我们设定的假设函数是H=1/(1+e^(-KX))这个值在0-1之间,可以当作概率
def H(Xi):
global K
y=np.dot(K, Xi.T)
if y>0:
return 1/(1+np.power(np.e,-y)) # xi需要转置,才能得到内积和
else:#为负数的时候,对sigmoid函数的优化,避免了出现极大的数据溢出
return np.power(np.e, y) / (1 + np.power(np.e, y))
# 代价函数L=求和((H(x)-y(x))^2),其中H是关于K矩阵中所有系数参数的函数
# 代价函数就是你估算的值与实际值的差的大小,使得代价函数最小,这样就能不断逼近结果
# 使得代价函数最小,就要使得初始点在斜率线上不断往低处移动,呈现出系数的不断微小移动
# 固定公式格式,推导原理看吴恩达P11
def dL_K(): # 代价函数对矩阵中系数参数k求导
global X, Y, K, m, n
dL_Karr = np.empty(n) # 数组用来存放L对每个k求导后的结果
for j in range(n):
ans = 0
for i in range(m):
ans += ((H(X[i]) - Y[i]) * X[i][j]) # 由于k的系数是x,所以求导后还要乘x
dL_Karr[j] = ans
return dL_Karr
def itreation(time): # 迭代,使O1,O2的代价函数趋于最低点
global K
for i in range(time):
# 一次迭代过程中代价函数对系数k的导数数组
dL_Karr = dL_K()
# 同时变化,减法原因是正斜率使得O更小,负斜率使得O更大,不断往低处移动即代价函数最小
K = K - A * dL_Karr
if (i % 10000 == 0): # 每100次输出一次
print(f"迭代了{i}次,变量的系数矩阵K为{K}")
if __name__ == "__main__":
print("X",X)
print("Y",Y)
itreation(time)
print('归一化系数(第一个是常数)', K, )
# 注意归一化所求的系数矩阵K是(X-U)/S的系数,真正系数,需要将x参数前面的系数合并
#计算真正的X
X[:,1:]=(X[:,1:]+U)*S
# 忽略前一位常数,计算真正系数
K[1:] = K[1:] / s
# 利用真正系数,计算真正常数
K[0] = K[0] - np.sum(K[1:] * u)
print('真正系数矩阵', K)
#绘图,注意x轴是确定参数x1,y轴是确定参数x2
x1=X[:, 1]
x2=X[:, 2]
#画出决策界线,分界线是x2作为y轴,x1作为x轴,KX=0的线
#构造网络
x=np.linspace(-1,5,1000)
y = np.linspace(-1, 5, 1000)
x,y=np.meshgrid(x,y)
#每个k对应的规则在28行输出可以看出来,第一二三行已经确定
z=K[0]+K[1]*x+K[2]*y+K[3]*np.power(y,2)+K[4]*np.power(y,3)+K[5]*x*y+K[6]*x*np.power(y,2)+K[7]*np.power(x,2)+K[8]*np.power(x,2)*y+K[9]*np.power(x,3)
plt.contour(x,y,z,0)
plt.scatter(x1[Y==0], x2[Y==0],c='r',marker='x')
plt.scatter(x1[Y==1], x2[Y==1],c='g',marker='o')
plt.xlabel("x1")
plt.ylabel("x2")
plt.show()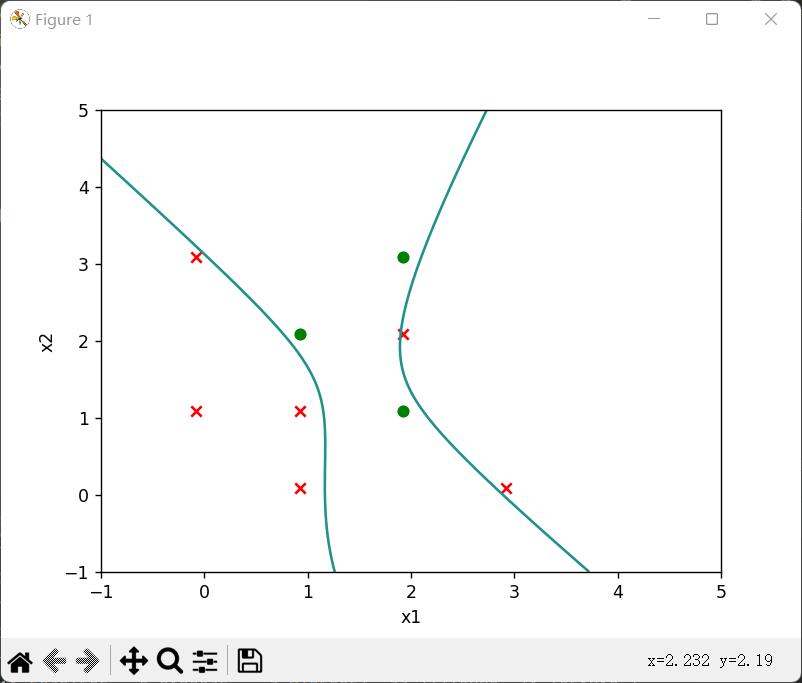
再给他加一个数据
import numpy as np
import matplotlib.pyplot as plt
# 全局变量
# 生成数据
#X每一行代表了x1,x2的值,并且相应对应下面y的分类
X =np.array([[0,1],
[1,1],
[1,0],
[1,2],
[2,1],
[3,0],
[0,3],
[2,2],
[2,3],
[3,2]])
# Y中的数据量等于X矩阵的行数,二分类,Y只能取0,1
Y = np.array([0,0,0,1,1,0,0,0,1,1])
#构造模拟的曲线次方
power=3
#获取变量默认为俩个变量
for i in range(power+1):
for j in range(power+1):
#通过俩个变量x1,x2构建高次函数
if(i+j<=power&i+j>1):
newX=np.power(X[:,0],i)*np.power(X[:,1],j)
print("x1次方",i,"x2次方",j)
X=np.append(X,np.array([newX]).T,axis=1)
# 开始
# 学习率,在代价函数斜率线上移动的距离步子大小
A = 0.1
# 迭代次数
time = 100000
# 进行归一化操作
# 获取每列平均值
u = np.average(X, axis=0)
# 获取没列的标准差
s = np.std(X, axis=0)
# 按行复制,构成X同形状矩阵
U = np.repeat([u], len(X), axis=0)
S = np.repeat([s], len(X), axis=0)
# 归一化,注意归一化所求的系数矩阵K是(X-U)/S的系数,真正系数,需要将x参数前面的系数合并
X= (X - U) / S
# X矩阵中第一列加入x0=1参数,便于构建常数项
X = np.insert(X, 0, np.ones((1, len(X))), axis=1)
# 数据个数
m = len(X)
# 参数个数
n = len(X[0])
# 系数变量K矩阵就是多元参数的系数,就是我们要递归的重点变量,先给这个矩阵的每个值都赋予初始值1
K = np.ones(n)
# 输出
print(f"有{n}个参数,就是X列数+常数项所乘的单位1")
print(f"有{m}条数据,就是加常数后X行数")
# 假设函数
# 在逻辑回归中我们设定的假设函数是H=1/(1+e^(-KX))这个值在0-1之间,可以当作概率
def H(Xi):
global K
y=np.dot(K, Xi.T)
if y>0:
return 1/(1+np.power(np.e,-y)) # xi需要转置,才能得到内积和
else:#为负数的时候,对sigmoid函数的优化,避免了出现极大的数据溢出
return np.power(np.e, y) / (1 + np.power(np.e, y))
# 代价函数L=求和((H(x)-y(x))^2),其中H是关于K矩阵中所有系数参数的函数
# 代价函数就是你估算的值与实际值的差的大小,使得代价函数最小,这样就能不断逼近结果
# 使得代价函数最小,就要使得初始点在斜率线上不断往低处移动,呈现出系数的不断微小移动
# 固定公式格式,推导原理看吴恩达P11
def dL_K(): # 代价函数对矩阵中系数参数k求导
global X, Y, K, m, n
dL_Karr = np.empty(n) # 数组用来存放L对每个k求导后的结果
for j in range(n):
ans = 0
for i in range(m):
ans += ((H(X[i]) - Y[i]) * X[i][j]) # 由于k的系数是x,所以求导后还要乘x
dL_Karr[j] = ans
return dL_Karr
def itreation(time): # 迭代,使O1,O2的代价函数趋于最低点
global K
for i in range(time):
# 一次迭代过程中代价函数对系数k的导数数组
dL_Karr = dL_K()
# 同时变化,减法原因是正斜率使得O更小,负斜率使得O更大,不断往低处移动即代价函数最小
K = K - A * dL_Karr
if (i % 10000 == 0): # 每100次输出一次
print(f"迭代了{i}次,变量的系数矩阵K为{K}")
if __name__ == "__main__":
print("X",X)
print("Y",Y)
itreation(time)
print('归一化系数(第一个是常数)', K, )
# 注意归一化所求的系数矩阵K是(X-U)/S的系数,真正系数,需要将x参数前面的系数合并
#计算真正的X
X[:,1:]=(X[:,1:]+U)*S
# 忽略前一位常数,计算真正系数
K[1:] = K[1:] / s
# 利用真正系数,计算真正常数
K[0] = K[0] - np.sum(K[1:] * u)
print('真正系数矩阵', K)
#绘图,注意x轴是确定参数x1,y轴是确定参数x2
x1=X[:, 1]
x2=X[:, 2]
#画出决策界线,分界线是x2作为y轴,x1作为x轴,KX=0的线
#构造网络
x=np.linspace(-1,5,1000)
y = np.linspace(-1, 5, 1000)
x,y=np.meshgrid(x,y)
#每个k对应的规则在28行输出可以看出来,第一二三行已经确定
z=K[0]+K[1]*x+K[2]*y+K[3]*np.power(y,2)+K[4]*np.power(y,3)+K[5]*x*y+K[6]*x*np.power(y,2)+K[7]*np.power(x,2)+K[8]*np.power(x,2)*y+K[9]*np.power(x,3)
plt.contour(x,y,z,0)
plt.scatter(x1[Y==0], x2[Y==0],c='r',marker='x')
plt.scatter(x1[Y==1], x2[Y==1],c='g',marker='o')
plt.xlabel("x1")
plt.ylabel("x2")
plt.show()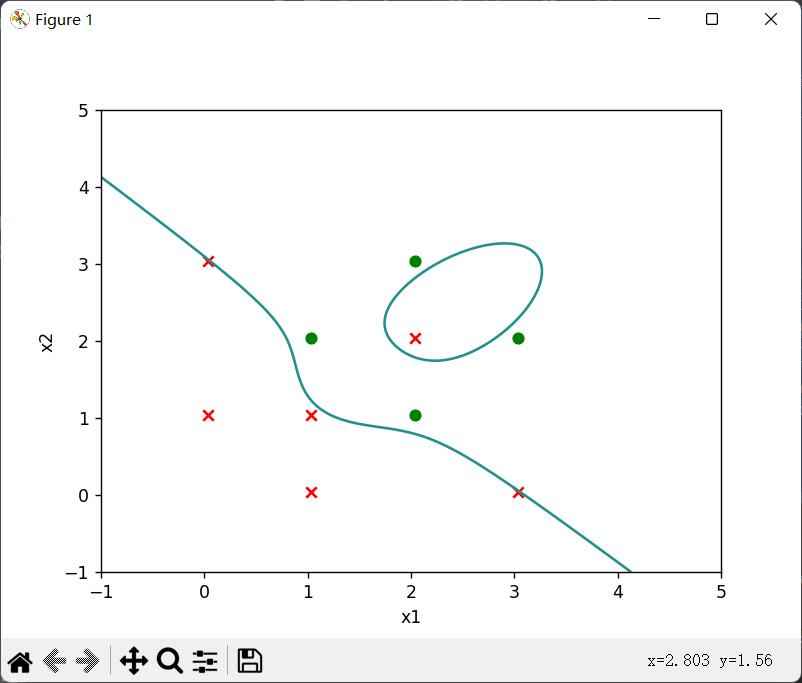























 600
600











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










