面向柔性作业车间动态调度的深度强化学习

姓名：Renke Liu, Rajesh Piplani & Carlos Toro (2022) 

题目：Deep reinforcement learning for dynamic scheduling of a flexible job shop

期刊：International Journal of Production Research, 60:13, 4049-4069

DOI: 10.1080/00207543.2022.2058432
文章结构：第二节综述了动态调度的发展和最新研究，以及强化学习在调度中的应用。

第3节明确了研究问题和研究目的。

第4节介绍了解决DFJSP的一种方法。

第5节给出了数值实验结果以及与基准解的比较。

第6节强调了我们的贡献，并讨论了未来的研究方向。

研究问题：

模型：动态（工件持续到达）柔性作业车间             算法：DDQN双深度Q网络

目标：最大限度地减少所有工件的累积延误

问题描述：一个柔性的作业车间包含多个工作中心，每个工作中心可能有多台机器。所有工件都必须按照预定的独特工序访问每个工作中心一次。在分层分布式调度系统中，调度决策由分别隶属于每个工作中心和机器的路由代理和排序代理做出；

 符号概念

(1) 工件jobs：J = {Ji : i = 1, ... , n} 是 n 项工作的集合。, n} 是 n 个工作的集合。
(2) 机器Machines：M = {Mk : k = 1, ... , m} 是 m 台机器的集合。, m} 是 m 台机器的集合。
(3) 工作中心 Work centres：W = {Wl : l = 1, ...Wl={Ma，...，Mz}。, Mz}；一台机器只能属于一个工作中心。
(4) 序列和操作：工作 Ji 需要 ni 个操作 OJi = [O1 i , ... , Oni i ]，由操作序列 Sqci = [W1 i , ... , Wni i ]的机器提供服务。
Wj i 表示需要处理操作 Oj i 的工作中心。完成率 Pi 是已处理操作数与 ni 的比率。
(5) 处理时间Processing time ：ti,k 表示 Ji 在机器 Mk 上的处理时间。tji表示 Oj i 的预期处理时间，计算公式为

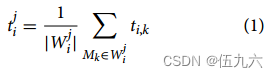
 PTJi = {t j i : j = 1, ... , ni} 是 Ji 的所有操作的预期处理时间集合。

 (6) 机器队列和可用时间：Jk = {Ja，......, Jz} 是机器 Mk 当前排队待处理或正在处理的作业集合，COk 表示 Mk 当前运行开始后的时间；AMk 是 Mk 的可用时间，AWl 是工作中心 Wl 的平均可用时间，计算公式为 

(7) 待处理时间（TTD）、剩余处理时间和松弛时间：NOW 表示系统当前时间；Di 表示作业 Ji 的到期日；作业的 TTD 是其到期日与 NOW 之间的差值。
然后，作业的松弛时间 Si 是其 TTDi 减去 Ri，即所有剩余作业的预计处理时间之和。这些值的计算公式为

其中，x 是 Ji 即将进行的操作的指数。TTDi、Ri 和 Si 的值随着生产的推进而变化 

(8) 绩效衡量：Ci 是 Ji 的完成时间，一项工作的迟到时间 Ti 的计算公式为

 总迟到时间 Tsum、最大迟到时间 Tmax 和迟到率的计算公式为

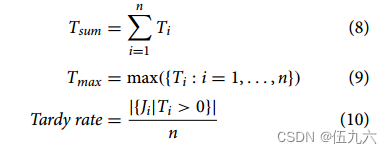
验证方案和目标

 影响生产性能的因素有三个。

(1) 作业到达率：作业到达率越高，机器利用率越高，系统拥塞越严重。

(2) 作业和机器的异质性（不均匀性）：作业在不同机器上的处理时间和截止日期的紧迫性各不相同。
此外，作业开始处理序列后，其剩余工作、松弛时间和到期时间也会随时间变化。机器的工作量和可用性也各不相同。

(3) 到期日紧张度：作业的 TTD 放宽会导致总延迟时间和平均延迟时间降低，因为作业在拥堵情况下有更多的松弛时间（平均）可以使用。此外，如果系统中作业的关键性不同，调度器可以利用一些作业的高松弛时间来保护更关键的作业。
基于这些观察结果，我们引入了三种场景进行训练和验证：

(1) 预期到达率/利用率：我们调整作业到达率，使其与系统的预期利用率相匹配。假设 E(t) 是所有机器上所有操作的预期处理时间，E(interval) 表示作业到达之间的预期时间间隔。假设 m 台机器均匀分布在所有 w 个工作中心，则系统的预期利用率可计算为 

在指定预期利用率之后，可以计算到达之间的预期时间。让我们假设随机变量X表示作业到达之间的时间间隔遵循指数分布:X ~ Exp(β)， β = E(间隔)。
值得一提的是，预期利用率的计算是基于恒定和平稳到达的假设，以及相同的工作。在实际操作中，由于机器的到达间隔时间、操作顺序和处理时间的随机性，一些闲置的能力是不可避免的。本研究假设预期利用率为90%，以近似于繁忙工厂的生产。

加工时间的异质性（不均匀性）:加工时间ti,k取自均匀分布:ti,k ~ U[Low, High]。我们考虑了两种平均处理时间相同的场景:(1)高异质性场景:ti,k ~ U[5,25]，其中最大时间是最小时间的5倍;(2)低异质性情景:ti,k ~ U[10,20]，其中最大时间仅为最小时间的两倍。

 截止日期紧度:在创建作业Ji时，分配一个与预期总处理时间成比例的原始TTD。原TTD、原闲置时间和到期日计算为

比值αi表示作业Ji的到期日紧度。
      我们考虑两种紧密度情景:(1)高到期日期紧密度:αi ~ U[1,2]，其中作业的平均原始松弛时间为其总加工时间的一半;(2)交货期紧度低:αi ~ U[1,3]，平均原始松弛时间等于作业的总加工时间。
       使用四种场景组合:(1)高非均质性和高密性:HH([5,25]/[1,2]);(2)高非均质性、低密性:HL([5,25]/[1,3]);(3)低非均质性、高密闭性:LH([10,20]/ [1,2]);(4)低非均质性和低密性:LL([10,20]/[1,3])。

       最小化所有工作的累积延迟是本研究的主要目标;此外，还在附录中提出了延迟率和最大延迟率，以对该方法进行全面评估。

 解决方法

双 DQN 被用作系统中两类智能体的学习器：(1) 路由代理，连接到每个工作中心，在作业到达时为其选择机器；(2) 排序代理，连接到每台机器，在机器闲置且发现队列中有多个作业时选择一个作业进行处理。

状态表示

 本研究关注的是一个随着时间推移而大量未知工作到达的制造系统。

       我们使用抽象信息而不是特定于工作的特征来构建状态空间。作业的数量只影响计算，而不影响产生的抽象数据的维度。下面介绍一些相关的符号:

(1)JNOW = {Ji|Ri > 0}是当前系统中存在的作业的集合，可以用来衡量系统中的拥塞情况;

(2) AJl是当前正在被其他机器处理并将到达工作中心的作业集合，这些作业的到达时间集合为ATl;

(3)对于Jk中的工作，其后续工作中心的集合记为SWk 

RA的状态空间由三类特征组成:

(1)工作中心内的机器信息;

(2)拟派遣工作的情况;

(3)即将到达的工作信息。

状态特征详情见表1; 为工作中心的每台机器收集三种类型的特征(标记为“*”)。对于控制工作中心Wl的RA，其状态空间大小为|Wl| × 3 + 3。

SA的状态空间：作业的到达和离开会不断改变 SA 的队列规模。因此，收集所有作业的某些类别信息会产生一个维度可变的状态空间。在这项工作中，我们使用抽象化和通道化的数据来总结排队作业和系统的信息，从而创建一个稳定的状态空间。
二十五个特征按其类型和大小分为六个通道，详情见表 2。

 动作表示

 RA 而言，可用的行动简单地对应于在工作中心内选择机器。

 SA 来说，不断变化的队列使得直接选择作业变得不可行，因此我们选择了四条排序规则作为行动空间的构建模块，以实现间接作业选择：

(1)最短加工时间(SPT):选择迫在眉睫的加工时间最短的作业。
(2)排队作业(WINQ):选择其后续生产阶段排队作业处理时间总和最小的作业。WINQ规则倾向于均匀分配系统中的作业
(3)临界比(Critical Ratio, CR):选择TTD与剩余加工时间之比最小的作业。CR规则的缺点是其不一致性。当可用作业尚未延迟时，CR规则倾向于TTD较小且剩余处理时间较长的作业。
另一方面，如果可用作业已经延迟，则CR规则优先考虑延迟时间最高(TTD最小)和剩余处理时间最短的作业。
(4)最小松弛(Minimum Slack, MS):选择松弛时间最小的作业。如果作业尚未过期，则此规则的行为类似于CR规则，优先考虑TTD较短且剩余处理时间较长的作业(因此较短的松弛时间)，并在作业延迟时保持一致。

奖励函数

以延迟最小化为调度目标，自然的奖励机制是使用已实现的工作延迟作为该工作所经历的所有ra和sa的联合奖励信号。然而，多智能体强化学习的研究表明，尽管智能体可以从联合奖励中学习以实现共同目标，但它们可能会收到来自队友行为的虚假奖励信号(Sunehag et al . 2017);这种挑战被称为多智能体信用分配问题。取而代之的，开发了一种替代方法，奖励智能体对作业排队的贡献.

图2显示了一个包含三个操作的作业的生产历史示例。作业到达车间时的初始持续时间TTD大于其操作时间的总和，这就留下了一些空闲时间作为排队缓冲。空闲时间随着作业排队等待处理而逐渐消耗;如果一个作业在其处理完成之前消耗了所有空闲时间，则会导致延迟。

 

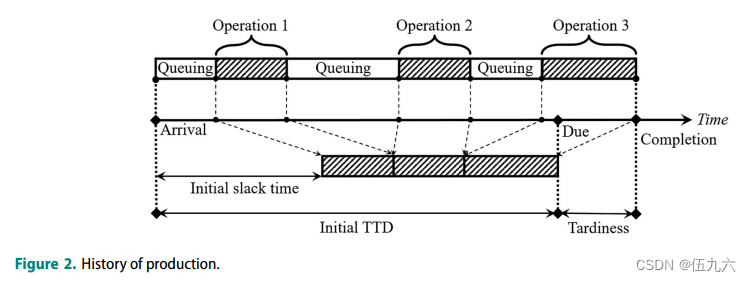
 预防和减少拖延就等于在生产的各个阶段都节约了空闲时间。然而，奖励临时目标并不总是可取的，因为代理可能会学习一种最大化奖励而忽略实际目标的策略(Kuhnle, Schafer et al 2019)。为了确保训练的成功，必须考虑几个方面。

首先，奖励功能需要平衡相互冲突的目标，因为追求不同的延迟相关目标可能会导致不希望的结果。例如，当系统被大量到期日很紧的新到达作业所淹没时，与其他规则相比，SPT规则显著减少了延迟作业的总和和延迟作业的比例，但以最大延迟为代价，因为它“牺牲”了处理时间长的作业，而优先考虑时间较短的作业，而不考虑其重要性。为了提高绩效，必须给予一个公正的奖励，在本研究中，这个奖励是累积延迟。 

 其次，奖励必须与系统级绩效保持一致。为了避免信用分配问题，RA 和 SA 在训练时主要根据本地信息做出决策；奖励也是根据单个操作而不是最终的延迟情况来计算的。训练成功的关键在于确保奖励与整体绩效之间的一致性，即通过追求短期奖励来提高系统级绩效

此外，保留所有作业的空闲时间是非常困难的，尤其是在系统拥挤或截止日期紧迫的情况下。考虑到这一点，更合理的做法是量化作业迟到的可能性，并将这一因素纳入奖励计算。对于作业 Ji，我们使用一个 sigmoid 函数将其松弛时间 Si 转换为临界系数 Fi，以消除异常值（过大的值）：

 Fi ∈ (0, 2)，其中 β 是用户指定的系数，用于调整 sigmoid 函数的曲率；随着 β 值的增大，sigmoid 函数会变得更加平滑。

基于上述考虑，我们提出了两种松弛驱动的奖励函数

RA 的替代奖励函数：RA 需要评估所有机器的可用性和适用性，并将作业分配给一台能最大限度减少长期累计延迟的机器。当作业 Ji 到达工作中心 Wl 完成第 x 个作业时，可以计算出作业完成后（时间步长 t + 1）的估计松弛时间，即 E(St+1 i )，它是剩余处理时间和机器可用时间的函数。

 实际松弛时间 St+1 i 在操作完成后实现：

 奖励的计算方法是，与估计的松弛时间相比，实际松弛时间的增减，并根据工件的关键系数进行调整。

 SA 的替代奖励函数：SA 需要对排队作业进行优先排序，并选择一个能将长期累积延迟时间降至最低的作业。奖励可以从排队暴露的角度来解释：当机器 Mk 及其队列 Jk 的 SA 选择一项作业 Js 时，它以延长其他作业的排队时间为代价结束所选作业的等待，同时将所选作业暴露在其后续工作中心 Ws 的排队中。
我们将节省或延长的排队时间称为空闲时间的增减。对所选工件松弛时间的增减定义为其他工作的平均处理时间（按 Js 临界系数调整）减去后继工作中心调整后的可用时间：

未被选中的工件的平均空闲时间损益等于 Js 的处理时间（根据其关键度系数的平均值进行调整）减去其后续工作中心的调整后平均可用时间。 

 δ 是一个调整可用时间大小的系数，因为它通常比处理时间大几倍；如果不做这一调整，代理就会过度关注后继工作中心的工作量。最终奖励的计算公式为

 为奖励计算选择一个合适的 β 和 δ 值对训练的成功至关重要。通过粗略搜索，我们发现 40 <β< 60 和 δ = 0.2；一般来说，在异质性较低的情况下，使用较小的β来训练的代理表现更好。

状态转移

我们提出了一种异步过渡方法，以配合替代奖励塑造函数。如图 3 所示，过渡从时间步骤 t 的决策点开始，到时间步骤 t + 1 的操作完成时结束。时间步长 t + 1 不一定与下一个决策点重合。 

 

 参数及训练

分布式调度体系结构本质上是一个多智能体系统。在本研究中，我们采用参数共享技术和集中训练和分散执行训练方案(Gupta, Egorov, and Kochenderfer 2017)，在训练阶段将多智能体问题简化为单智能体问题。具有相似范围和目标的智能体共享神经网络参数，并从公共经验池中学习，从而产生相似和合作行为。其他drl相关参数如表3所示。

两种类型的智能体都在由三个工作中心（每个工作中心有两台机器）组成的柔性作业车间中接受训练。RA 和 SA 的训练是分开进行的，以避免非平稳性。训练过程模拟了 100,000 个时间单位的生产，期间约有 12,400 个工作到达车间。模拟和训练过程如图 4 所示

 许多特征的值，尤其是与工作数量和时间相关的特征，远远超出了普通激活函数能够产生平滑且可区分梯度的范围。我们使用实例归一化技术（Ulyanov、Vedaldi 和 Lempitsky，2016 年）来处理数据，以避免梯度消失问题。至于神经元，由于负值在状态空间中很常见，因此使用 tanh（双曲正切）函数作为激活函数。采用 Huber 损失作为损失函数。学习率从 10-2 衰减到 10-3。随机梯度下降（SGD）被用作 ANN 的优化器，动量设置为 0.9。表 3 列出了网络的超参数。

 用于 RA 和 SA 的 ANN 架构如图 5 所示。在 SA 的双分支结构中，由于通道 5 和 6 中的抽象数据具有合适的大小，因此实例归一化层只处理通道 1 至 4 中的数据。

 制造系统的仿真模型由开源 Python 离散事件仿真库 SimPy（Matloff，2008 年）实现。ANN由Python机器学习库PyTorch（Paszke等人，2019年）实现。训练在配备英特尔酷睿 i5-4210H 2.90 GHz CPU 和 12 GB 内存的个人电脑上进行。RA 和 SA 的训练损失记录分别见图 A-11 和 A-12。

实验

实验分为三个阶段:

(1)独立效用测试，测试SA和RA在指定场景下的独立效用，并根据基准规则在累积延迟(主要目标)上的表现确定进入第二阶段实验的基准规则。

(2) 基于第一阶段结果的综合 DRL 测试，使用若干排序和路由规则组合来验证综合 SA 和 RA 的性能。此外，还比较了近期基于 DRL 的 DFJSP 解决方案和基于 GP 的 DFJSP 解决方案。

(3) 可扩展性测试：研究 RA 和 SA 在更大规模系统中的性能，并验证其可扩展性。

      在每个验证方案下，通过 100 次模拟运行（每次运行包含多次迭代）测试优先级规则和算法的性能。每次运行都会创建一个唯一的生产事件；作业到达之间的时间间隔、每台机器上的处理时间以及作业的到期日紧迫性都是从各自的统计分布中得出的。为了进行公平比较，生产事件会反复应用于由 DRL 代理或基准规则控制的系统。每次迭代持续 1000 个单位时间，平均有 124 个作业到达 。使用以下性能指标对性能进行评估：

(1) 归一化性能（NP）：以优先规则为基线，规则或算法在运行中的归一化性能计算公式为

 NP 衡量性能增益；正值意味着性能优于基线，越高越好。NP 在下面各图的".1 "面板中显示；提出的DRL方法的均值用绿点线表示。

 (2) 成功率：规则或算法导致累计迟到时间最少的运行百分比。
它衡量了调度策略对各种生产事故的适应性，以及与其他策略相比的优越性。为了更好地展示所提出的 DRL 方法相对于基准规则的性能，我们在下图中分别在 "2 "和 "3 "面板中显示了使用和未使用 DRL 代理的成功率。

独立效用实验

路由智能体

本节以表 4 中列出的六种著名路由规则为基准，测试了 RA（DRL-RA）的独立效用。它们都与先进先出（FIFO）排序规则相结合，以最大限度地减少排序决策的影响；最早可用（EA）路由规则是基准规则。

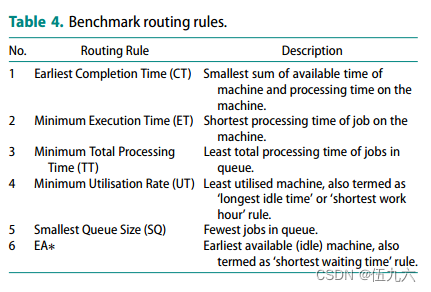
 图 6 总结了数值实验的结果。在每个方案中，排名前两的基准规则（基准线除外）用星号标出；性能低于基准线的规则用叉号标出。

 路由策略之间的差异是决定性的，提出的 DRL-RA 严格优于所有基准路由规则。一个有趣的现象是，作为主动作业分配效应最小的基准规则，EA 规则的性能优于大多数路由规则，在进入 DRL 综合实验阶段的两个低异质性场景中，成为第二好的基准规则。更详细的结果见表 A-6。

 排序智能体

在本节中，SA（DRL-SA）和其他排序规则与 EA 路由规则相结合。除了用于构建行动空间的四种规则外，我们还在基准池中加入了其他九种著名的排序规则，这些规则旨在改善与延迟相关的目标，还有六种复合规则在最大限度减少迟到方面表现出色。完整列表如表 5 所示；FIFO 规则是基准规则。数值实验结果如图 7 所示。在每种情况下，前五条基准规则用星号标出；性能低于基准的规则用叉号标出。

 

 规则的排名在四种情况下有所不同，这表明合理排序决策的属性在不同环境下会发生变化；利用有限车间信息的排序策略无法适应所有情况。另一方面，归一化性能的差异很小；即使是最好的规则或算法，其性能比基线提高的幅度也不到 30%，因此胜率分布相当均匀。即使是性能中等的规则，也能在某些运行中获胜。

另一个跨场景的观察结果是，参数化更复杂的奇异规则和 MOD、PTWINQS 和 DPTLWKRS 等复合规则的性能更优，这一点是一致的。

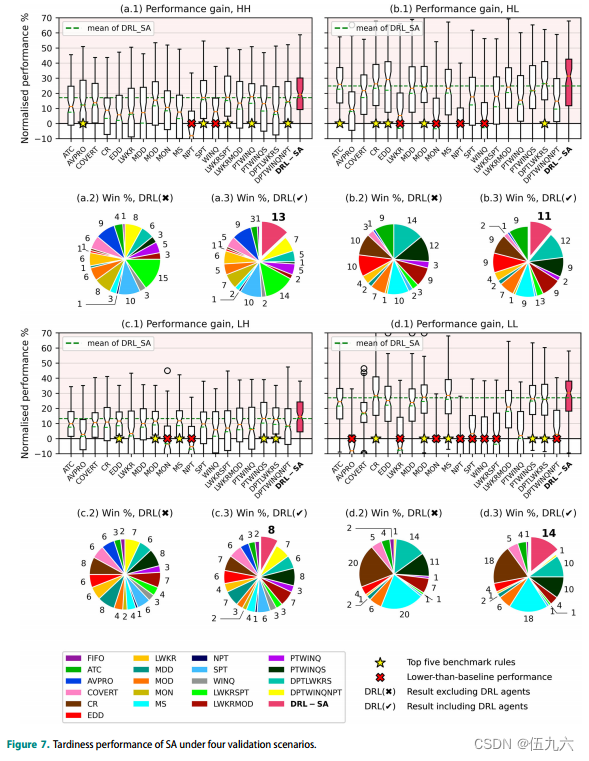
在所有场景中，提出的的 DRL-SA 都优于大多数规则；在每个场景中，它都比最佳基准规则高出约 4% 的性能。有 DRL 代理和无 DRL 代理的胜率比较表明，提出的方法并不是简单地模仿特定规则的行为，而是在所有验证实例中都保持良好的性能，并持续击败其他规则。更详细的结果见表 A-7。 

集成DRL验证

在这个部分，训练有素的RA和SA被整合到一起，以控制所有的工作中心和机器来解决DFJSP。为了验证它们之间的协同效应，我们还让RA和SA独立并行运行。

根据前一节的结果，我们选择了前两个路由规则和前五个排序规则，创建了十个基准组合，其中 FIFO+EA 为基准。此外，还包括两个由 GP 生成的新规则组合，分别称为 GP1（Zhang, Mei, and Zhang 2019）和 GP2（Zhang et al 2020a）。

鉴于 DRL 算法的决定性优势，与基于表格 RL 的方法进行比较是不公平的，因此基准范围仅限于基于 DRL 的 DFJSP 解决方案，这使得可与之进行比较的研究寥寥无几。其中包括两种同行方法作为基准，分别称为 Lang 2020（Lang et al 2020）和 Luo 2020（Luo 2020）。

基于元启发式的方法不用于比较，因为它们缺乏处理动态作业到达的能力，不能应用于实时调度。
结果如图8所示;具体结果如表A-8所示。

 路由决策比排序决策对系统性能的影响更大，调度策略之间的差异受组成路由规则的影响比受排序规则的影响更大。

这种现象一方面与调度代理参与决策的频率有关：在分层调度架构下，一项作业必须分配给一台机器，但可以在没有排序决策的情况下进行处理。此外，路由决策可以更好地利用处理时间和工作量的异质性。好的路由决策可以避免过长的操作和排队时间，而排序决策只能在不可改变的容量和需求的限制下重新安排作业顺序。

在四种情况下，集成 DRL 优于所有基准规则组合、基于 DRL 的同行解决方案和基于 GP 的解决方案。并行独立运行的 RA 和 SA 的性能也验证了它们作为集成方法组成部分的实用性；虽然 SA 的优势不如 RA 那么明显，但它们都有助于提高集成 DRL 的性能；缺少其中任何一个，性能都会下降。

可扩展性

 在本节中，测试了所提出的方法对配置更改的敏感性。RA和SA分别在两个可伸缩性测试中运行。

 更高柔性测试

在柔性测试中，每个工作中心的机器数量都有所增加。由于工作中心的配置发生了变化，输入/输出规模也发生了变化，因此对 RA 进行了重新训练；训练损失记录分别如图 A-13 和 A-14 所示。为简化演示，只比较了 5.1.1 节中每个验证方案下的前两个基准规则和基线（EA 规则）。每个工作中心 3 台机器的测试结果（平均 180 个作业到达）如图 9（a）至（d）所示；每个工作中心 4 台机器的测试结果（平均 240 个作业到达）如图 9（e）至（h）所示。

柔性扩大了路由规则之间的差异，表明作业分配的替代方案既可能是优势，也可能是劣势。利用作业处理时间和机器工作量信息的 CT 规则得益于灵活性的提高，即使有更多的作业到达，也能获得更好的归一化性能和更低的累计迟到率。DRL-RA 和 CT 规则的优越性在柔性系统中更加明显；它们都能在处理时间高度异构的情况下将累计延误时间降至极低水平，尤其是当工作中心的机器数量达到四台时。表 A-9 显示了更多有关累计迟到时间结果的信息。

然而，柔性系统的性能提升是以降低DRL-RA的胜率为代价的。当系统柔性的开发超过了高利用率时，延迟的发生更多地是由于作业到达率的波动，而不是由于路由决策的质量。

 更长序列测试

为了测试更长的工艺序列，操作(工作中心)的数量增加到6个和9个。
由于输入/输出大小的同质性，我们导入5.1.2节中训练好的模型作为初始参数(而不是随机初始化)来加速学习。然后对SA进行再训练以适应新环境;培训损失记录分别如图A-15和图A-16所示。在每个验证场景下，只比较5.1.2节中的前五个基准规则和基线(FIFO规则)。图10 (a)至(d)栏中显示了6道工序试验的结果，图10 (e)至(h)栏中显示了9道工序试验的结果。

 

 当操作次数增加时，所有排序规则的性能增益都略有增加；SA 的性能仍然优于或至少与最强基准规则的性能相匹配。另一方面，SA 与强基准规则之间的差异对配置变化不敏感；这一现象与 Holthaus 和 Rajendran（1997 年）的观点一致，即排序规则的相对性能不受制造系统规模的显著影响。表 A-10 提供了更详细的结果。

结论

 用双DQN算法训练的两类调度代理，无论是作为独立组件还是以集成方式部署，都优于现有的调度策略;调度代理提供的优势即使在系统配置发生变化时也能保持。除了提高绩效外，本研究的主要贡献还包括:

(1)特殊化表示:动态调度面临规范不断变化的问题，现有机器学习(ML)算法的静态架构无法处理。目前的研究大多是假设将调度问题限制在一个固定的规模。本研究提出抽象状态特征和间接动作表示来解决这一问题。由此产生的方法可以管理长时间和大量作业的调度问题。
(2)基于知识的奖励塑造:与DRL取得巨大成功的通常任务(如桌面游戏和电子游戏)不同，大多数生产计划和控制问题不能被制定为“获胜”或“生存”的任务，而是专注于本质上复杂的目标的约束优化。基于领域知识的奖励形成对于在解决方案质量和实现成本之间取得平衡至关重要。
为了提高训练效率，鼓励调度代理之间的合作，本研究开发了一种替代奖励塑造技术。它比简单的联合奖励方法提供更高的稳定性和性能，使我们的工作具有良好的可重复性。
(3)高效的训练和应用:轻量级神经网络保证了毫秒级延迟的快速决策，使实时控制成为可能。我们提出的架构也显示出良好的训练效率:100,000个单位的模拟时间(训练)最多需要20分钟才能完成，这使得快速迭代能够适应动态环境。调度代理可以通过整合新的体验来重放记忆或调整参数，从而快速获得新的行为。尽管所提出的体系结构在小型制造系统中得到了验证，但在更强大的计算能力的支持下，其效率有望在更大规模的系统中保持不变。

      将 DRL 研究成果应用于生产领域既是挑战也是机遇：与 DRL 取得巨大成功的应用中的表格或图形状态表示法不同，工业数据是杂乱无章和非结构化的。特征的选择、抽象和预处理仍然需要人类的专业知识。在 ML 研究中引入创新的数据解释技术可以促进这一过程。此外，车间是一个复杂的环境，考虑更多类型动态事件（如随机处理时间和机器故障）的研究将有助于使 DRL 更接近实际应用。
人工奖励塑造依赖于领域专业知识，需要花费大量精力进行设计和微调。此外，行动可能会产生持久而广泛的影响，这很难用标量奖励来评估。将因果学习和推理与 RL 结合起来，以确定行动及其影响之间的关系，是一个热门的研究课题，其在工业应用中的潜力令人期待。
网络物理制造系统中智能代理之间的合作行为还没有得到很好的研究。事实证明，合作多代理 RL 的其他流行技术，如代理之间的通信（Foerster 等人，2016 年）和自动值分解（Sunehag 等人，2017 年），在提高多代理系统的性能方面也很有价值；但它们在动态调度中的应用仍有待探索。

文献综述

 最近的数据驱动方法

传统方法面临着效率与质量的两难选择。在动态事件频繁发生的环境中，最优时间表的有效性可能会迅速下降，元启发式方法的高计算成本使其效用大打折扣。另一方面，基于规则的方法由于决策过程中涉及的信息类型有限且数学运算简单，因此能产生接近实时的解决方案，但却以质量为代价。
最近的研究旨在开发排程策略，通过将耗时的开发过程转移到离线状态，并将开发的策略应用于在线决策，从而利用全面的车间信息在接近实时的情况下做出高质量的排程决策。一些候选方法包括遗传编程（GP）、监督学习和 RL。
GP 可用于制定优先级规则。传统的人工设计优先级规则只能利用有限的工作或机器信息，相比之下，GP 提供了一种将各种实时信息纳入决策的方法；通过迭代、基于群体的随机进化，规则的制定实现了自动化。
早期的研究通过将排序规则与通用路由规则相结合，将 FJSP 简化为 JSP（Ho、Tay 和 Lai，2007 年；Pickardt 等人，2010 年）。最近，GP 也被用于路由和排序规则的共同演化。Yska、Mei 和 Zhang（2018）提出了合作协同进化 GP（CCGP）框架，用于在两个独立种群中进化路由和测序规则。

Zhang、Mei 和 Zhang（2018 年）提出了多树 GP（MTGP）架构，以利用路由和排序规则之间的相互作用。还有一些研究旨在通过特征选择提高性能（Zhang, Mei, and Zhang 2019; Zhang, Mei et al 2020）。基于 GP 的方法通过将更广泛的特征/信息作为输入，确实提高了所制定规则的有效性；但是，其决策仍然依赖于简单的计算和逻辑运。

替代方法是参数化复杂的技术，如监督学习算法。这些算法应用于调度的关键假设是，最佳调度知识可以通过人工神经网络（ANN）、支持向量机（SVM）和决策树等参数化算法学习到。监督学习算法通过分析优化或基于梯度的方法来提高解决方案的质量，与进化方法相比，能更快地收敛到令人满意的解决方案。
ANN 主要用于优先规则选择。Mouelhi-Chibani 和 Pierreval（2010）提出了一种由实时事件触发的动态规则选择机制，以解决动态流动车间调度问题；Guh、Shiue 和 Tseng（2011）提出了一种自适应规则选择机制，可定期为柔性制造系统中的不同工作中心分配不同的优先规则。

还有一些研究旨在寻找最佳工作顺序。Weckman、Ganduri 和 Koonce（2008 年）将 JSP 分解为一系列面向工作的分类问题，并使用 GA 生成的最佳时间表来训练 ANN。Zang 等人（2019 年）也将 JSP 分成几个子问题，由具有并行全连接层和卷积层的混合网络来解决。
Gupta、Majumder 和 Laha（2019 年）提出了一种方法，可以找到工作在最优计划中的相对位置，而不是直接制定最优序列。
其他监督学习应用包括使用决策树从最优日程表中学习策略（Olafsson 和 Li，2010 年；Jun、Lee 和 Chun，2019 年），以及使用 SVM 作为自适应规则选择器（Shiue，2009 年；Priore 等，2010 年）。 

基于强化学习的调度 

与其他主要为分类任务开发的监督学习算法相比，DRL 算法可以建立从环境观察到行动的直接映射；由于利用了人工神经网络（ANN）作为价值或策略表示，DRL 算法还具有处理复杂数据的能力。这两个特点使 DRL 成为数据密集型制造系统生产控制的理想候选方法。

此外，动态调度问题可以表述为符合马尔可夫决策过程（Markov Decision Process，MDP）定义的离散时间随机控制过程（Zhang、Xie 和 Rose，2017 年）。更具体地说，在分布式调度代理采取的反应策略下运行的车间，可以被模拟为一个分散的马尔可夫决策过程（DEC-MDP）（Bernstein 等人，2002 年）。动态调度问题的马尔可夫性质使 RL（MDP 中的一种顺序决策工具）适用于解决调度问题。
早期的研究使用表格 RL 算法来执行全系统调度（Wang 和 Usher，2005 年；Aissani、Beldjilali 和 Trentesaux，2008 年），其中状态空间包含抽象的系统信息；行动是在一组优先级规则中进行选择，以应用于系统中的所有机器。将调度问题分解为几个复杂度较低的子问题，并用独立的 RL 代理来解决每个问题也是可行的（Wang 等，2020 年）。
为了更好地处理高维输入空间，DRL 算法已被纳入全系统调度架构，例如使用 DQN（Lin 等人，2019 年）、DDPG（Liu、Chang 和 Tseng，2020 年）和 PPO（Park 等人，2021 年）来解决 JSP。
附属于每台机器或工作中心的 RL 算法也可以是分布式决策者。Gabel 和 Riedmiller（2012 年）将 JSP 描述为一个分散的马尔可夫决策过程，具有不断变化的行动集和部分有序的过渡依赖关系，并提出了一种策略梯度方法来解决它。Lang 等人的研究（2020 年）也采用了类似的方法，通过 DQN 训练的两类调度代理独立执行作业排序和机器选择，以管理灵活的作业车间。
为解决固定规模调度问题而开发的方法很难推广到不同类别的任务。此外，很少有动态调度研究不限制任务的规格。

一些研究针对特定环境下的调度，因此有专门的状态和动作表示。
Waschneck 等人（2018）提出了一种 DQN 方法，用于调度半导体制造设施中不同位置之间的批次移动。Qu、Wang和Jasperneite（2019）提出了一种去中心化的行为批判方法，用于向服务器分配作业。Kuhnle、Röhrig 和 Lanza（2019）在半导体生产设施中开发了基于 TRPO 的自主订单调度系统。Shi 等人（2020）提出了一种在离散制造系统中转移作业的 DQN 方法。Hubbs 等人（2020 年）提出了一种深度行为批判方法，用于在具有非确定处理时间的化学制造系统中进行调度；Malus、Kozjek 和 Vrabič（2020 年）提出了一种多代理方法，用于管理车间中的自主移动机器人。Yang 和 Xu（2021 年）提出了一种 A2C 方法，用于管理具有动态作业到达的可重构生产系统。
Luo 等人（2021 年）提出了一种 PPO 方法，用于解决受机器、工具和工人等多种资源限制的动态工作车间问题。
工作也可以是决策实体。Bouazza、Sallez 和 Beldjilali（2017）提出了一种 Q-learning 方法，让智能产品为其访问的每个工作中心和机器选择机器选择和作业排序规则。Baer 等人（2019）将柔性制造系统建模为一个 Petri 网（Zhou，2012 年），在这个 Petri 网中，附属于单个产品的 DQN 代理决定前往不同机器的路线。
基于 DRL 的动态调度仍是一个新颖的研究领域，发表的论文很少。本研究采用了最通用的情境--灵活的作业车间，以获得更好的可移植性和可比性。下一节将介绍问题的正式定义。