
算法基本复现了论文,也有自己的一些设计,希望有参考价值, 可自行修改数据进行新的算例测试,所有参数均可改
车间调度系列文章:
-
24、柔性车间调度丨论文复现:强化学习算法求解柔性车间问题
柔性车间调度问题
柔性车间调度问题可描述为:多个工件在多台机器上加工,工件安排加工时严格按照工序的先后顺序,至少有一道工序有多个可加工机器,在某些优化目标下安排生产。柔性车间调度问题的约束条件如下:
-
(1)同一台机器同一时刻只能加工一个工件;
-
(2)同一工件的同一道工序在同一时刻被加工的机器数是一;
-
(3)任意工序开始加工不能中断;
-
(4)各个工件之间不存在的优先级的差别;
-
(5)同一工件的工序之间存在先后约束,不同工件的工序之间不存在先后约束;
-
(6)所有工件在零时刻都可以被加工。
数学模型
数学模型参考文献:
[1]NAIMI R, NOUIRI M, CARDIN O. A Q-Learning Rescheduling Approach to the Flexible Job Shop Problem Combining Energy and Productivity Objectives[J]. Sustainability, 2021, 13(23)
本文的模型约束参考上面论文,目标函数修改为下面这个:

结果展示:
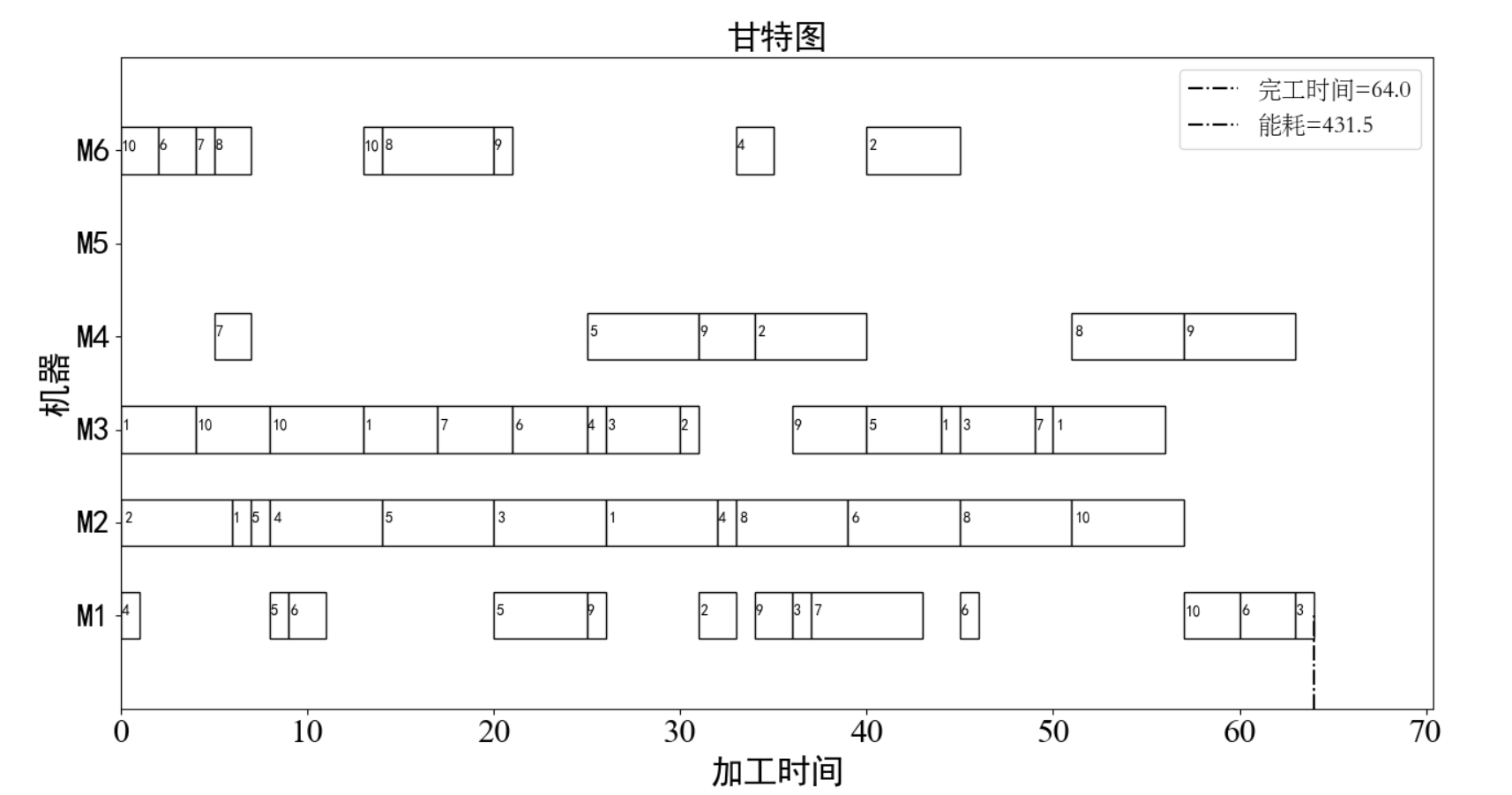
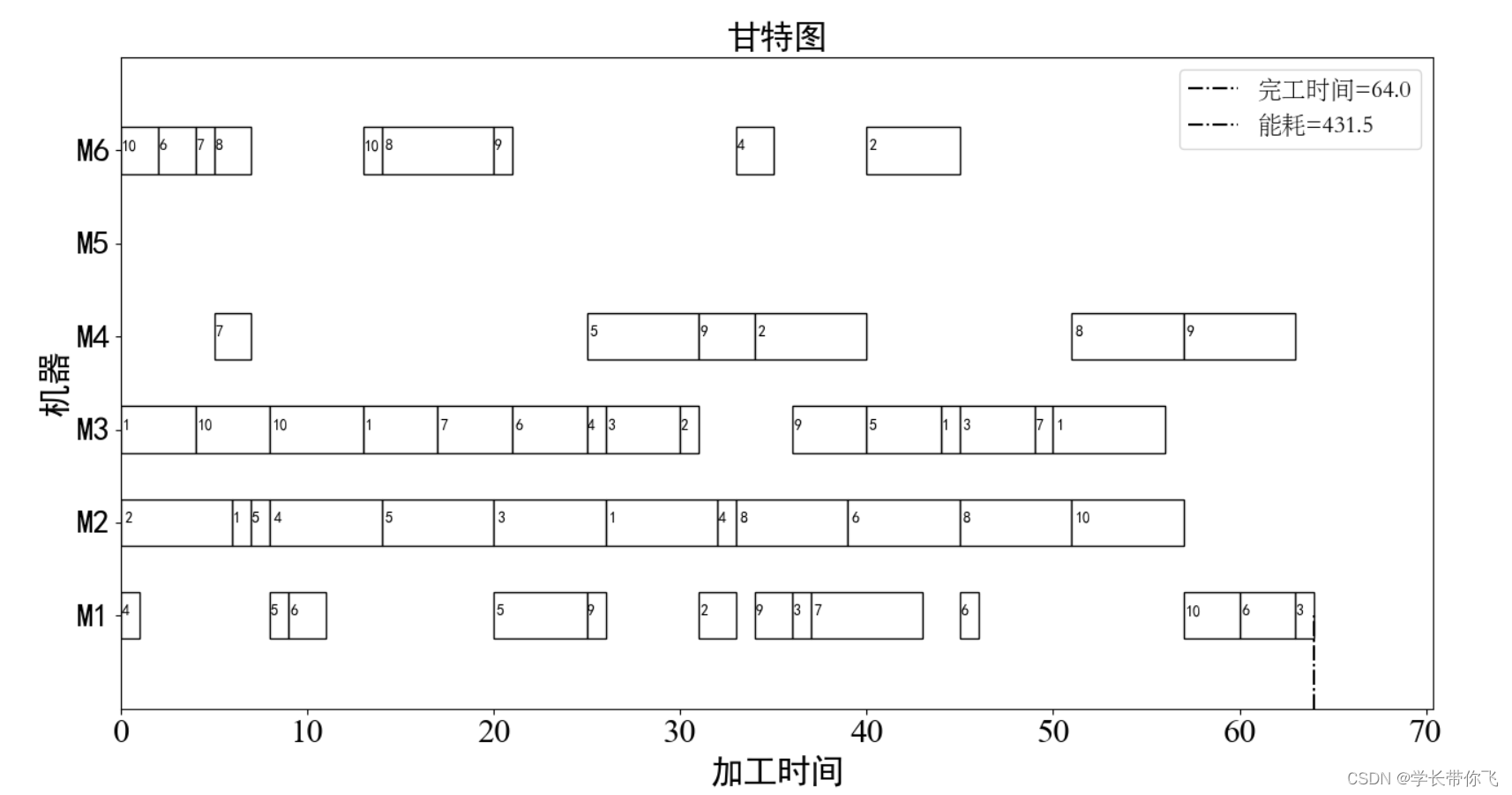
最优完工时间方案:
最优能耗方案:
完工时间迭代次数的变化图如下:
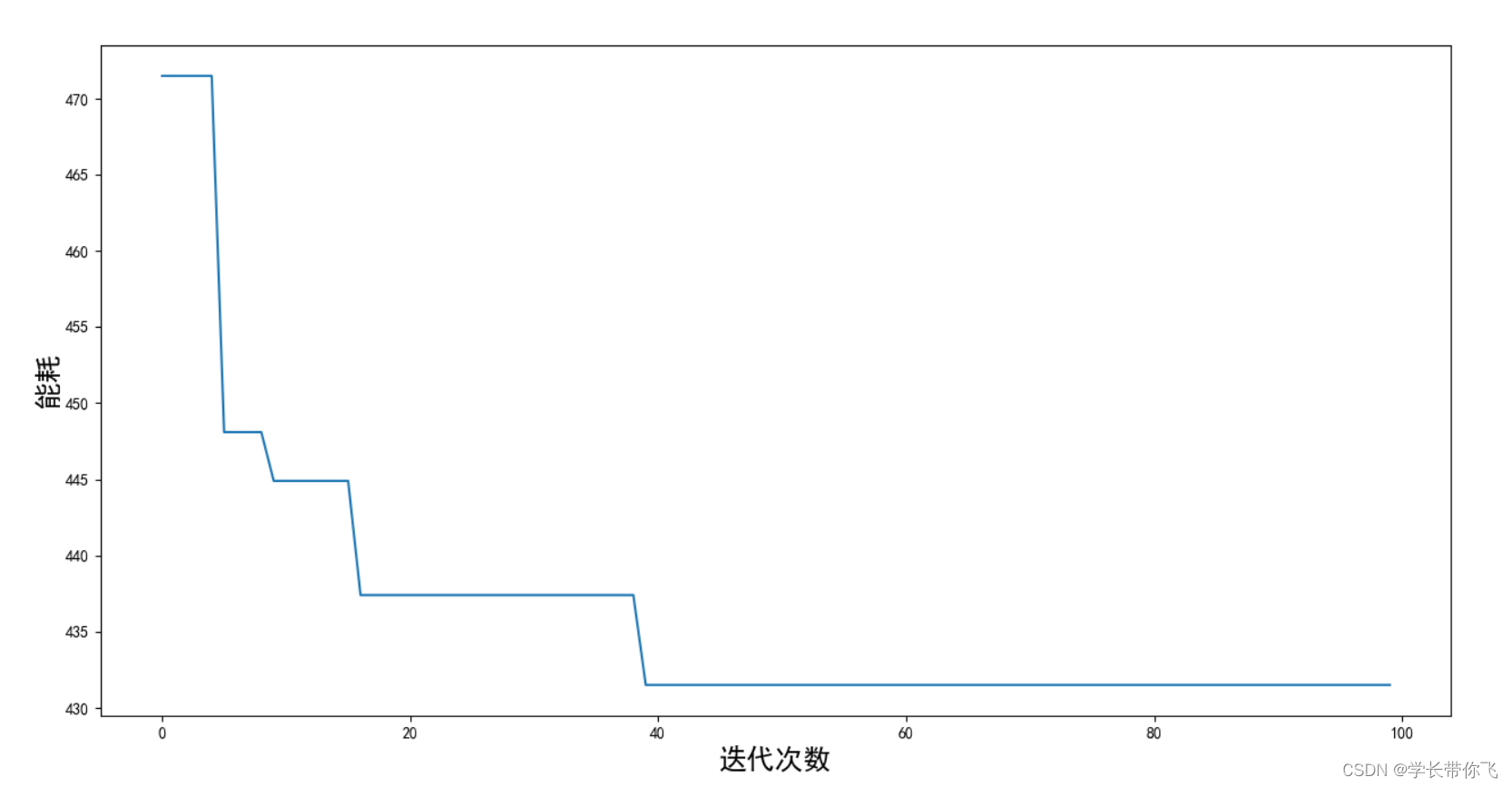
能耗迭代次数的变化图如下:
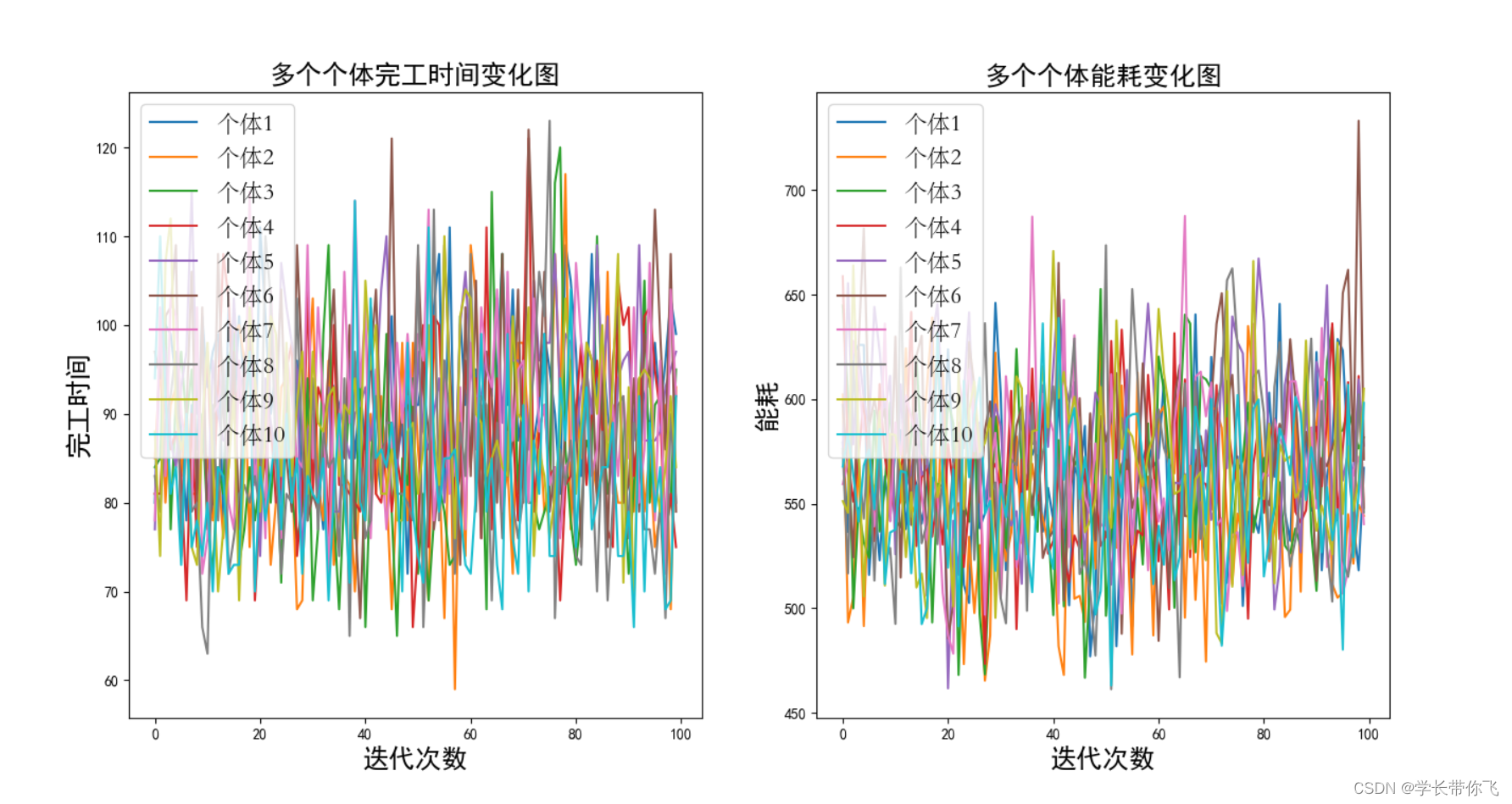
q学习对种群前10个体指标优化情况:
代码运行环境
windows系统,python3.6.0,第三方库及版本号如下:
pandas==0.25.3
numpy==1.18.5
matplotlib==3.2.1
第三方库需要在安装完python之后,额外安装,以前文章有讲述过安装第三方库的解决办法。
Q学习算法
Q学习算法是在价值行为算法,即通过每一步动作返回的价值指导下一步的动作。为避免算法出现局部最优,通常设置一个接近1贪婪选择概率,低于该概率在算法设置的策略进行动作选择,否则随机选择动作。对于存在环境与主体互动的问题,Q算法的求解就是把问题抽象成为一个马尔可夫决策过程。
文献的算法介绍及公式:
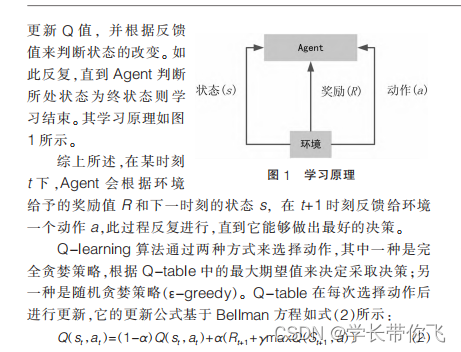
算法理解:
-
1)Q表初始化,行是状态,列是状态的动作,值是对应状态下的对应行为预估的奖励。
-
2)每次更新智能体状态时,一定概率下选择最大奖励的动作,否则随机选取动作。
-
3)动作选择完后根据奖励更新Q表(估计值)
参考博客:https://blog.csdn.net/qq_35164554/article/details/106620571
Q学习算法详解
数据处理:
文章以mk01为例,主要是提取出excel表格工件的加工信息和和生成按顺序排列的初始工序编码:
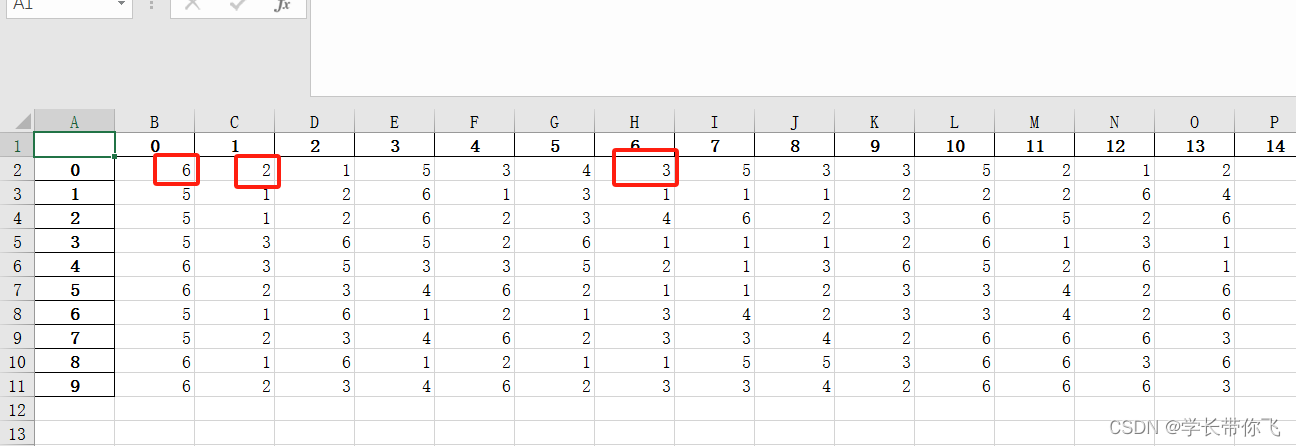
6表示工件1有6道工序,2表示工件1的第一道工序有2个可加工机器,是1和3,加工时间是5和4, 同理:3表示工件1的第二道工序有3个可加工机器,是5、3、2,加工时间是3、5、1。其余工件工序依次类推。
提取编码:
import re
def deal(df):
work = []
Tmachinetime = []
for i in range(len(df)):
row = [int(re.findall(r'[0-9]+',str(df.iloc[i,j]))[0]) for j in range(df.shape[1]) # 提取每一行的数字
if str(df.iloc[i,j]) != 'nan']
wor = [i+1 for w in range(row[1])] # 每一行是一个工件,对应row的第二个数是工序数
work += wor # 记录工序
row1 = row[2:] # 第三个数开始提取工序加工信息
while row1:
signal = row1[0] # 第一个数是工序的可加工机器数
Tmachinetime.append([])
for j in range(signal): # 提取对应工序的加工机器和加工时间
mt = row1[2*j+1:2*j+3]
Tmachinetime[-1] += mt
row1 = row1[2*signal+1:] # row1提取完的信息截取掉,都提完后,row1变为[],跳出循环
return [work, Tmachinetime]
按顺序排列的初始工序编码结果:
work = [1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 9, 10, 10, 10, 10, 10, 10]
所有工件工序加工情况:
Tmachinetime = [[1, 5, 3, 4], [5, 3, 3, 5, 2, 1], [3, 4, 6, 2], [6, 5, 2, 6, 1, 1], [3, 1], [6, 6, 3, 6, 4, 3], [2, 6], [3, 1], [1, 2], [2, 6, 4, 6], [6, 5, 2, 6, 1, 1], [2, 6], [3, 4, 6, 2], [6, 5, 2, 6, 1, 1], [3, 4, 2, 6, 6, 6], [1, 1, 5, 5], [6, 5, 2, 6, 1, 1], [2, 6], [3, 1], [5, 3, 3, 5, 2, 1], [3, 4, 6, 2], [5, 3, 3, 5, 2, 1], [6, 5, 2, 6, 1, 1], [2, 6], [1, 5, 3, 4], [2, 6, 4, 6], [3, 4, 2, 6, 6, 6], [3, 4, 6, 2], [1, 2], [3, 4, 2, 6, 6, 6], [2, 6], [6, 5, 2, 6, 1, 1], [1, 3, 4, 2], [6, 1], [1, 3, 4, 2], [3, 4, 2, 6, 6, 6], [2, 6, 5, 1, 1, 6], [3, 1], [3, 4, 6, 2], [3, 4, 2, 6, 6, 6], [6, 5, 2, 6, 1, 1], [2, 6], [2, 6, 4, 6], [6, 1], [1, 1, 5, 5], [6, 6, 3, 6, 4, 3], [1, 2], [3, 4, 2, 6, 6, 6], [2, 6, 4, 6], [3, 4, 6, 2], [3, 4, 2, 6, 6, 6], [5, 3, 3, 5, 2, 1], [6, 1], [2, 6, 4, 6], [1, 3, 4, 2]]
第一个[1, 5, 3, 4]是工件1第一道工序的加工情况,[5, 3, 3, 5, 2, 1]是第二道工序,具体的数字意义上面已经介绍。因为工件1是6道工序,所以第7个[2, 6]是工件2的第一道工序加工情况,其余依次类推。
工序编码生成:
文献是以随机生成的工序编码为先验知识:

对于本文,随机打乱上面的work即可:
def create_job(self):
job =np.copy(self.work)
np.random.shuffle(job) # 随机打乱固定初始工序编码
job = job.tolist()
return job
初始q表生成:
初始Q表生成,长度和工序编码一样,宽度是各个工序对应的可加工机器数,Q表初始值都是0,同时提取工序的对应加工机器和时间。
def create_Qtable(self):
qtable = []
m_all = []
t_all = []
for i in range(len(self.work)):
P = self.Tmachinetime[i] # 一行对应一个工序的加工信息
n_machine = [P[j] for j in range(0, len(P), 2)] # 偶数项取加工机器
n_time= [P[j] for j in range(1, len(P), 2)] # 奇数项取加工时间
m_all.append(n_machine)
t_all.append(n_time)
qtable.append([0 for j in range(len(n_machine))]) # 初始q表值都是0
return qtable, m_all, t_all
机器加工时间编码生成:
以工序编码为先验知识,q学习的状态是每一道工序,动作是对应工序的可加工机器的选择,一定概率下选择q值最大的动作(加工机器),否则随机选择动作。



def mt_choce(self,qtable, m_all, t_all):
machine, machinetime = [], []
choice_id = []
for i in range(len(self.work)):
q = qtable[i]
n_machine = m_all[i]
n_time = t_all[i]
if np.random.rand() > 1- self.ε: # 一定概率下选择最大q值对应的动作(加工机器)
idx = np.argmax(q)
else:
idx = np.random.randint(0,len(q),1)[0] # 否则随机选择动作
choice_id.append(idx)
machine.append(n_machine[idx]) # 提取对应时间的机器
machinetime.append(n_time[idx]) # 提取加工时间
return machine, machinetime, choice_id
q表更新:
奖励是总能耗分之一与完工时间分之一之和。

按照文献给的公式更新q表。
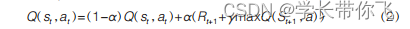
def q_renew(self, r, qtable, choice_id):
for i in range(len(choice_id)):
if i == len(choice_id)-1:
q_t1 = [0] # 最后一步设为0
else:
q_t1 = qtable[i+1] # 下一步的q值
idx = choice_id[i] # 动作索引
qtable[i][idx] = (1 - self.α)*qtable[i][idx] + self.α*(r + self.γ*max(q_t1))
# 更新
return qtable
解码:
每次安排工序加工必须考虑2个条件:
1、该工序的上一道工序是否完成
2、工序选择的机器是否空闲
步骤:
1、初始各个工件、各台机器的时间都是0;
2、读取一个加工工序和对应机器,取该工件的上一道工序结束时间(工件的第一道工序认为结束时间是0),该机器的上一道工序结束时间(机器的第一次加工工序认为结束时间是0)
3、取上一道工序结束时间,机器的上一道工序结束时间的最大值作为本工序的开工时间;
4、根据工序在机器的加工时间:更新对应工序的完工时间、机器的工序结束时间;
5、不断重复2、3、4,直到遍历到最后一个工序和机器编码,结束;
代码:
def caculate(self,job,machine,machine_time):
job_num = max(job)
machine_num = max(machine)
count = np.zeros((1, job_num),dtype=np.int)
jobtime=np.zeros((1, job_num))
tmm=np.zeros((1, machine_num))
tmmw=np.zeros((1, machine_num))
startime=0
list_M,list_S,list_W=[],[],[]
for i in range(len(job)):
svg = job[i] - 1
idx = self.work.index(svg + 1) + count[0, svg] # 读取对应工序的机器编码位置
sig = machine[idx]-1 # 取机器号
startime=max(jobtime[0,svg],tmm[0,sig]) # 工序结束时间,机器上一道工序结束时间的最大值
tmm[0,sig]=startime+machine_time[idx] # 更新对应工序的完工时间
jobtime[0,svg]=startime+machine_time[idx] # 更新机器的工序结束时间
tmmw[0,sig]+=machine_time[idx]
list_M.append(machine[idx])
list_S.append(startime)
list_W.append(machine_time[idx])
count[0, svg] += 1
tmax=np.argmax(tmm[0])+1 #结束最晚的机器
C_finish=max(tmm[0]) #最晚完工时间
trest=tmm-tmmw #空闲时间
E_all=sum((tmmw*self.p1)[0])+sum((trest*self.p2)[0]) #能耗计算
return C_finish, E_all,list_M,list_S,list_W,tmax
迭代设计:
Q学习是优化每个先验工序编码的机器选择。因为存在随机性,所以下次迭代的指标不一定优于上一次。记录每次迭代种群的最优个体,同时记录每个个体每次迭代的完工时间和能耗。
核心代码:
r = 1/E_all + 1/C_finish # 奖励
qtable = self.q_renew(r, qtable1, choice_id) # q值更新
Q_t[i] = qtable
work_job[i] = job
answer[-2].append(C_finish) # 记录每个个体的完工时间
answer[-1].append(E_all) # 记录每个个体的能耗
if C_finish < best_finish: # 如果完工时间低于最优完工时间
best_plan_finish = [job, machine, machinetime] # 更新最优完工时间方案
best_finish = C_finish # 更新最优完工时间
if E_all < best_Eall: # 如果能耗低于最优能耗
best_plan_Eall = [job, machine, machinetime] # 更新最优能耗方案
best_Eall = E_all # 更新最优能耗
结果
主函数:
import numpy as np
import pandas as pd
import data
from RL import rl_learn
import paint
df = pd.read_excel(f'./mk01.xlsx', sheet_name = 'Sheet1') # 打开mk01
parm_data = data.deal(df) # 处理表格得到的数据
parm_p = [[2, 1.7, 1.6,2.1, 2.4,4.1], [0.4,0.6,0.5,0.4,0.4,0.6]] # 负载功率和空载功率,可修改
ε = .5
α = 1
γ = .8
popsize = 100 # 种群规模
episode = 100 # 迭代次数
parm_rl = [ε, α, γ, popsize, episode] # 强化学习参数,可修改
rl = rl_learn(parm_data, parm_p, parm_rl)
best_plan_finish, best_plan_Eall, result_finish, result_Eall, answer = rl.total() # 强化学习结果
job, machine, machinetime = best_plan_finish[0], best_plan_finish[1], best_plan_finish[2] # 最优完工时间编码
C_finish, E_all,list_M,list_S,list_W,tmax = rl.caculate(job,machine,machinetime)
print('\n最优完工时间:', C_finish)
paint.draw_gantt(job, machine, machinetime, rl) # 画甘特图
job, machine, machinetime = best_plan_Eall[0], best_plan_Eall[1], best_plan_Eall[2] # 最优能耗编码
C_finish, E_all,list_M,list_S,list_W,tmax = rl.caculate(job,machine,machinetime)
print('最优能耗:', E_all)
paint.draw_gantt(job, machine, machinetime, rl) # 画甘特图
paint.draw_finsh(result_finish) # 最优完工时间迭代图
paint.draw_Eall(result_Eall) # 最优能耗迭代图
num = 10 # 种群的前num个体,num应小于popsize
paint.draw_change_finish(num, answer) # 记录q学习对各个个体的指标优化情况
结论
推文的算法的关键是,q学习对先验工序机器选择的优化。因为先验工序导致工序的解空间缩小,和q学习算法的一定随机性,指标不够优秀,q学习不够收敛,结果可能不太好。可以从增加种群个体数,增加迭代次数等方式进行优化,或者对q学习收敛图进行优化(只显示优于上次迭代的个体)。
组合优化问题,本质也是对最优组合进行寻找,算法收敛有时也不显得那么重要。不过也可能是q学习的参数问题,算法流程问题,或者q学习这种方式求解问题不太可行,需要更多测试和研究。
算法基本复现了论文,也有自己的一些设计,希望有参考价值, 可自行修改数据进行测试,所有参数均可改。
参考文献:基于Q-learning算…多目标柔性作业车间调度问题_李雅明
演示视频:
视频
柔性车间问题丨复现论文:强化学习求解柔性车间调度问题
完整算法+数据:
完整算法源码+数据:见下方微信公众号:关注后回复:调度

# 微信公众号:学长带你飞
# 主要更新方向:1、柔性车间调度问题求解算法
# 2、学术写作技巧
# 3、读书感悟
# @Author : Jack Hao
























 1076
1076

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








