有关皮卡序列中的一个理解小错误

有关皮卡序列中的一个理解小错误

前言

皮卡序列的迭代式如下：
$$y_{n+1}\left(x\right)=y_0+{\int }_{x_0}^{x}f\left(x,y_n\left(x\right)\right)dx$$
看似很容易实现，我有一个朋友，但是下面一串代码写的时候就没有注意，还想不明白！！！！！

问题代码

t=0;
for i=1:1:num
    y1(i)=integral(@(x) f(x,y0(i)),0,t);
    t=t+h;
end
t=0;
for i=1:1:num
    y2(i)=integral(@(x) f(x,y1(i)),0,t);
    t=t+h;
end
t=0;
for i=1:1:num
    y3(i)=integral(@(x) f(x,y2(i)),0,t);
    t=t+h;
end
t=0;
for i=1:1:num
    y4(i)=integral(@(x) f(x,y3(i)),0,t);
    t=t+h;
end
t=0;

问题原因

看似没有问题，但是其实后面是将y的部分直接乘以了积分区间，而非做积分。关键就在直接使用了y（i）上。

解决思路

这里写了一个新的数值积分函数，思路是在计算第一个皮卡序列的时候，已经确定了区间的长度，每一次迭代的次数其实也就对应着积分区间的数量，然后利用梯形积分即可得出结果：

function v=specialintegral(f,y,a,i,h)
    x=zeros(i,1);
    x(1)=a;
    ytemp=x;
    for j=2:1:i
        x(j)=h*j;
        ytemp(j)=f(x(j),y(j));
    end
    v=h/2*(ytemp(1)+ytemp(i));
    for j=2:1:i-1
        v=v+h/2*2*ytemp(j);
    end
end

最后得到的图像

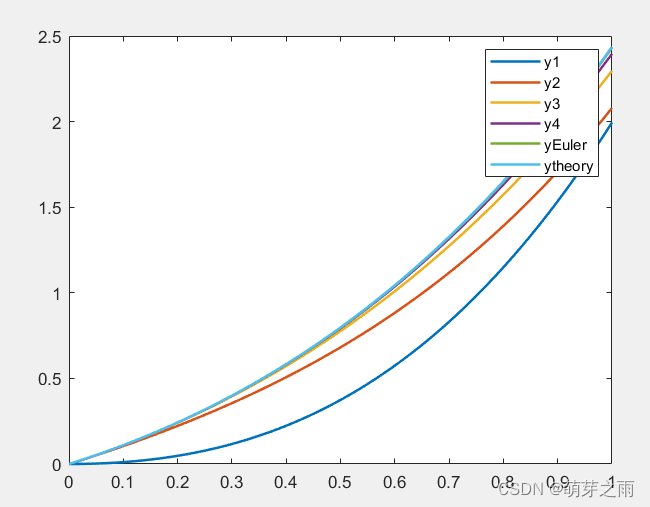
题目完整代码

整个题目完整的代码：

clear;
clc;
close all;

f=@(x,y) x+y+1; 
h=0.001;
num=1/h;
y0=zeros(num,1);
x=linspace(0,1,num);
x=x';
y1=zeros(num,1);
y2=zeros(num,1);
y3=zeros(num,1);
y4=zeros(num,1);


t=0;
for i=1:1:num
    y1(i)=integral2(f,0,t,0,t);
    t=t+h;
end
for i=2:1:num
    y2(i)=specialintegral(f,y1,0,i,h);
end
for i=2:1:num
    y3(i)=specialintegral(f,y2,0,i,h);
end
for i=2:1:num
    y4(i)=specialintegral(f,y3,0,i,h);
end

plot(x,y1,LineWidth=1.5);
hold on;
plot(x,y2,LineWidth=1.5);
hold on;
plot(x,y3,LineWidth=1.5);
hold on;
plot(x,y4,LineWidth=1.5);
hold on;


ytemp=zeros(num,1);
ytemp(1)=0;
a=0;
for i=2:1:num
    a=a+h;
    ytemp(i)=ytemp(i-1)+h*f(a,ytemp(i-1));
end
plot(x,ytemp,LineWidth=1.5);
hold on
funthe=@(x) 2*exp(x)-x-2;
ythe=funthe(x);
plot(x,ythe,LineWidth=1.5);

legend('y1','y2','y3','y4','yEuler','ytheory');

%% speicial integral
function v=specialintegral(f,y,a,i,h)
    x=zeros(i,1);
    x(1)=a;
    ytemp=x;
    for j=2:1:i
        x(j)=h*j;
        ytemp(j)=f(x(j),y(j));
    end
    v=h/2*(ytemp(1)+ytemp(i));
    for j=2:1:i-1
        v=v+h/2*2*ytemp(j);
    end
end

题目：

写在最后

真服了，这一个bug折腾了快一个小时。。。。。。。。。。，写在这里，愿有缘人可以不被折磨