捷联惯导基础知识之一（姿态更新的毕卡算法、龙格库塔算法、及精确数值解法）

一、介绍旋转矢量以及由旋转矢量更新四元数

• 等效旋转矢量微分方程(Bortz方程)：

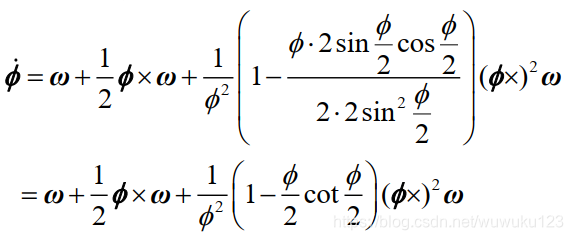
• 经过理论和近似推导：

• 单位四元数与旋转矢量关系：

• 单位四元数与三角函数的关系：

• 四元数更新方程：利用旋转矢量，考虑了不可交换性误差

其中四元数乘法表示为：

二、介绍毕卡级数，无限重积分项以及闭合解（定轴运动下）

以方向余弦矩阵的求解为例，介绍皮卡迭代法及毕卡级数；

• 1、定轴转动：两个坐标系相对转动，转动角速度方向始终不变；

因此，方向余弦矩阵离散化更新如下(满足定轴转动条件下):

假设IMU的运动是角运动，用一个多项式进行表示(常值、线性、抛物线、三次、四次角速度等)，并且根据陀螺仪角增量的输出，确定多项式的系数；

• 2、如果是非定轴运动，怎么求解毕卡算法？基于角运动假设的，有限项积分项的毕卡算法！

具体如何求解，就是下面将要说到的：“姿态更新的毕卡算法”

三、姿态更新算法：

1、姿态更新的毕卡算法

基本原理就是：先假定载体的角运动方式（如：常值、线性、抛物线、三次、四次角速度等），然后，再将

以四元数微分方程和毕卡级数解求解为例：

毕卡级数解：

然后根据假定的角运动形式，忽略毕卡级数解中的几重积分项；

习惯上：

• 一阶毕卡算法为常值角速度假设下的一阶级数展开算法；
• 二阶毕卡算法为线性角速度假设下的二阶级数展开算法；
• 三阶毕卡算法为抛物线角速度假设下的三阶级数展开算法；
• 四阶毕卡算法为三次曲线角速度假设下的四阶级数展开算法。
   

以线性角速度运动形式为例，得到二阶级数，四元数更新方程如下：

2、姿态更新的四阶龙格-库塔算法

标准四阶龙格-库塔算法求解，以四元数微分方程为例：

四阶龙格-库塔：

为了避免出现归一化误差(保证四元数是严格的单位四元数)，通常采取的方法是：

• 先求解等效旋转矢量的四阶龙格-库塔解，再利用旋转矢量进行四元数更新；
• 先求解等效旋转矢量的毕卡解，再利用旋转矢量进行四元数更新；

以等效旋转矢量的四阶龙格-库塔解为例子：

更新如下：

3、姿态更新的精确数值解法

前提是：角速度为多项式假设条件下获得姿态更新的精确数值解，在求解过程中隐含了对不可交换误差的精确补偿，姿态更新精度仅受限于计算机的数值解算精度。

 

四、总结：

从上面可以看出，上述的分析基于两点：

1、Bortz的等效旋转矢量微分方程（简化版）；

首先是Bortz提出了能够补偿不可交换性误差的等效旋转矢量微分方程；

然后假定IMU的运动为多项式角运动，也就得出旋转矢量的泰勒级数解；

然后根据圆锥运动的背景，得到圆锥误差补偿多字样算法；

泰勒级数解和圆锥误差补偿多字样算法：

圆锥误差补偿多子样算法与 基于泰勒级数展开的多子样算法， 理论上， 前者比后者更适合应用于圆锥运动环境， 而后者比前者更适合应用于多项式角运动环境。对于实际系统， 在角运动过程中， 通常认为多项式角运动只会短暂出现， 而更容易激发的是较长时间的周期性振动，它可近似为圆锥运动，因此实际中一般优先考虑采用基于圆锥误差补偿的多子样算法。 在圆锥运动假设条件下获得的圆锥误差补偿算法也常常称为多子样优化算法。

2、四元数或方向余弦矩阵微分方程的数值解，即微分方程左右两边积分；

在实际惯导系统中，任何连续且光滑的角运动，总可以用多项式进行近似描述。

（1）然后是假设角速度为不同形式的角运动(常值、线性、抛物线、三次、四次角速度等)，并忽略毕卡级数的几重积分项（根据假定的角运动进行裁剪），得到几阶毕卡算法；

习惯上所指的一阶毕卡算法为常值角速度假设下的一阶级数展开算法、 二阶毕卡算法为线性角速度假设下的二阶级数展开算法、三阶毕卡算法为抛物线角速度假设下的三阶级数展开算法、四阶毕卡算法为三次曲线角速度假设下的四阶级数展开算法。

（2）然后是四阶龙格-库塔算法:前提是角运动为 w=a+2*b*t 线性形式，且利用前一周期和当前周期，即【-T T】，

（3）然后是精确数值解法：首先假设不同形式的角运动，然后根据矩阵运算、卷积运算得到精确的数值解，精度取决于计算机数值解算精度。