目录
3) 齐次坐标(Homogeneous coordinates)
Lecture 04 • Transformation Cont.
1) Viewing Transformation(视图变换)
2) Projection Transformation(投影变换)
a) Orthographic projection(正交投影)
b) Perspective projection(透视投影)
Lecture 03 • Transformation
1) 为什么学习变换
变换可以使静态的物体平滑的运动起来,在动画、游戏等很多方面得到了广泛的应用
a) Modeling
变换包含物体自身的缩放、旋转、平移

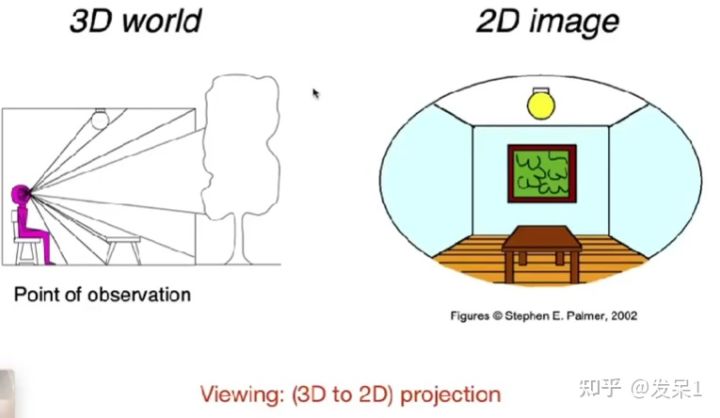
b) Viewing
变换还包含三维世界到一幅二维图像的投影(视口变换)
2) 二维变换
a) Scale(缩放)
通过一个对角矩阵可以将物体的x和y都缩放为原来的一半
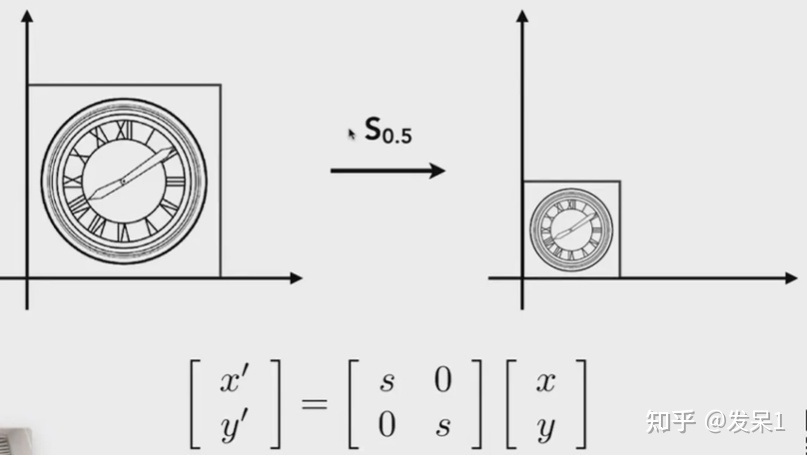
x和y也可以进行不均匀的缩放

我们还可以巧妙的实现“镜像”等效果

保持垂直方向不做变换,根据y值的不同,使点在水平方向变换的距离(在0和a之间)不同,可以做到切变(Shear)的效果

b) Rotate(旋转)
在未设定旋转轴和旋转方向时,旋转默认是绕原点逆时针旋转
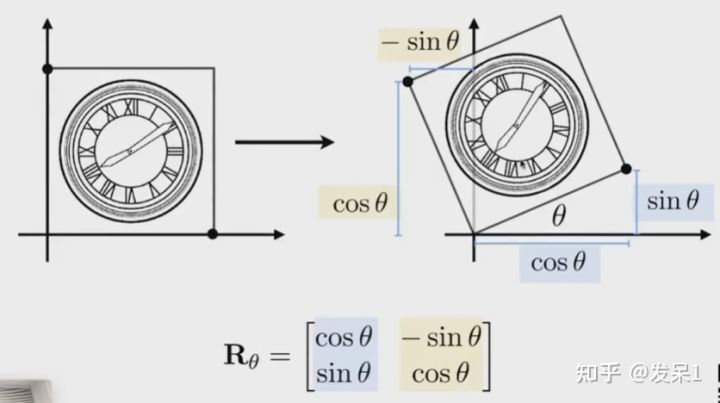
因为旋转矩阵对任一点都满足条件,所以我们可以取左上角和右下角这两特殊点的坐标,对它们的变换列方程组求解出矩阵公式
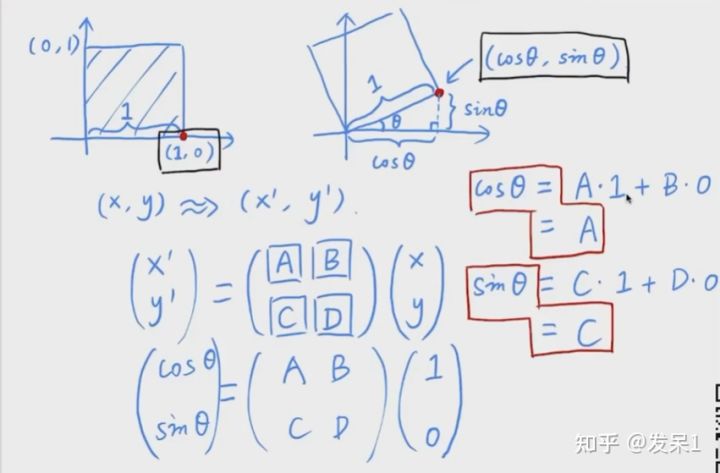
到这里我们可以发现,对一个坐标进行线性变换可以表示为坐标左乘一个同维矩阵
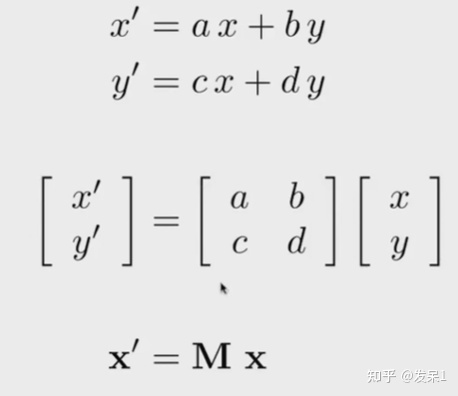
3) 齐次坐标(Homogeneous coordinates)
a) 为什么要引入齐次坐标
平移变换无法同旋转和缩放一起在一个变换矩阵中表示,只能单独补充(平移变换并不是线性变换),所以我们想设计一种方法使得三种变换在同一个矩阵中实现,而这一方法则通过齐次坐标完成

b) 齐次坐标的使用
通过增加一个w分量,我们便可以将三种变换在一个矩阵中实现,但应当注意的是,二维的点和二维的向量之间,w分量是有差异的

因为向量具有平移不变性,我们希望它的其它分量不会受到平移变换的影响,所以向量的w分量被定义为0。plus,将点和向量的w分量分别定义为1和0,使得我们做点和点之间,向量和向量之间,点和向量之间的运算时,w分量的运算也是有意义的(如一个点加上一个向量,结果仍是一个点,对应w分量为1+0=1,所得结果为1符合定义)
需要注意的是,从我们的经验看,点和点的相加是没有意义的(它们的w分量相加也不是1和0了),但是我们对此给出了定义:在齐次坐标的表示下,将一个点的所有分量同时除以w分量的值(w不为0)便可得到该点对应在笛卡尔坐标中的表示。这时,点和点相加获得的坐标在同时除以w分量的值后也就有了意义,即指两个点的中点(点和点相加可以指多个点)

结合前面所述,我们可以得到三种变换在齐次坐标下的表示

4) 逆变换(Inverse Transform)
逆变换指一个变换的逆过程,在数学上是乘以变换矩阵的逆矩阵

5) 变换的顺序
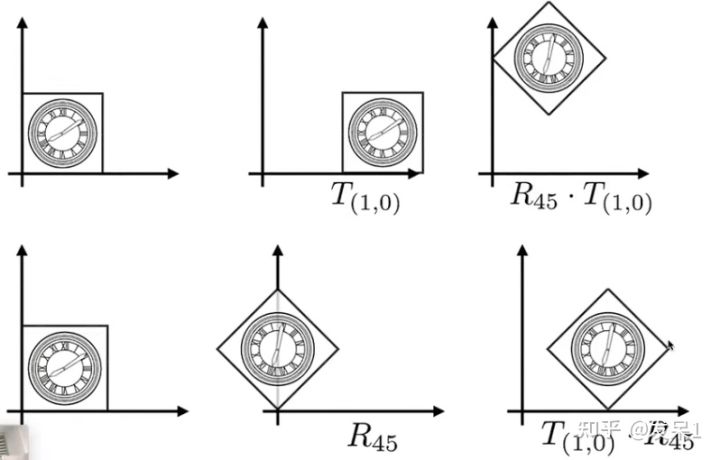
由上图我们可以看出,变化的顺序不同,得到的结果是不同的。这一点也和矩阵的乘法有关(矩阵乘法不满足交换律)

因为我们一般使用的是列向量,所以矩阵需要左乘列向量,则我们在乘上变换矩阵时应当从右向左依次相乘(如下图)

对于一些复杂的变换,我们可以将其拆解,比如使得物体绕一个给定点c旋转:先将物体平移至原点,绕原点旋转,再逆变换平移回去
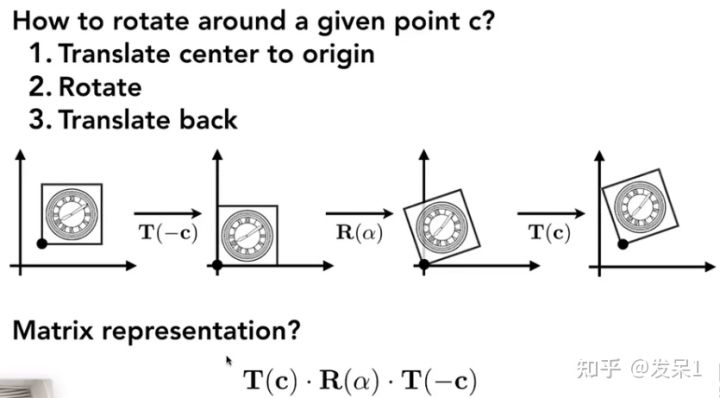
6) 三维变换
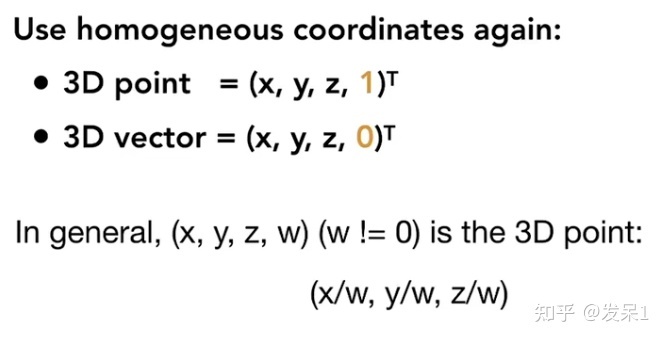

三维变换同二维变换很像,只是多了一个z分量
a) 变换公式
缩放和平移
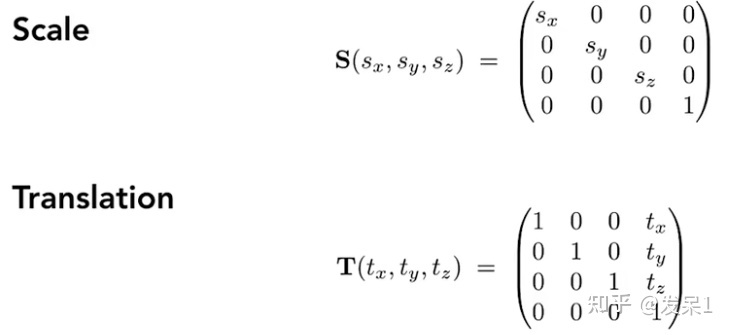
绕不同轴旋转(我们可以发现公式中的规律:矩阵中旋转轴对应的行和列不变,绕y轴的旋转矩阵因叉乘的方向会和其他两个有所差异)

b) 三维的旋转
三维空间中旋转的任一角度都可以用三个参数roll、pitch、yaw来表示
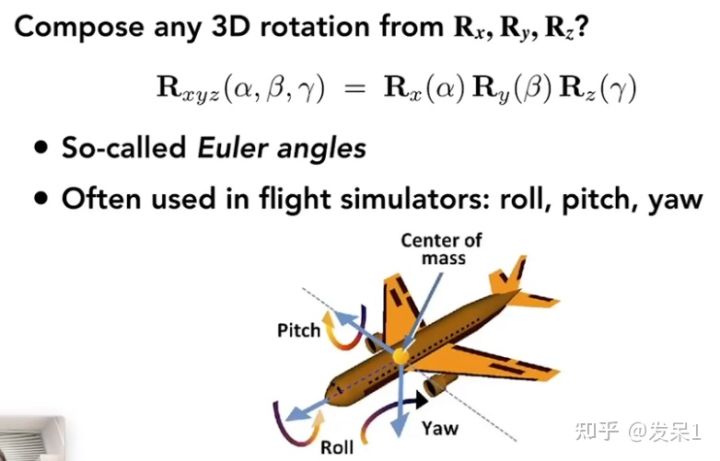
这里引入了Rodrigues Rotation Formula(罗德里格旋转公式)表示绕任一旋转轴n旋转ɑ角度的矩阵(旋转轴n未过原点时可以先将其起点平移到原点)
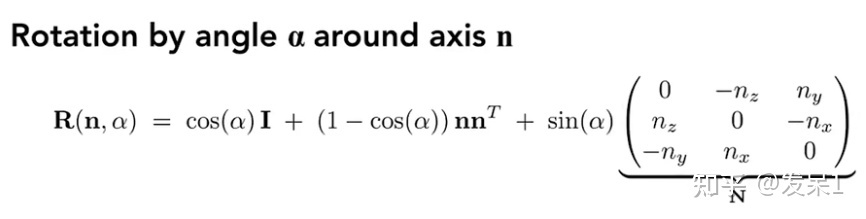
Lecture 04 • Transformation Cont.
补充
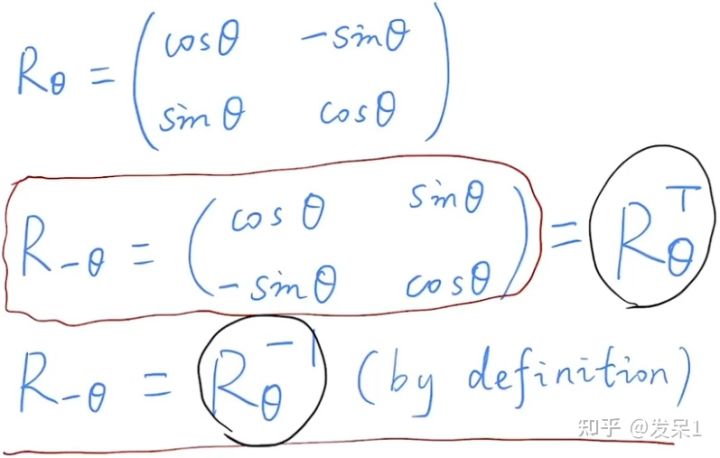
对于上一节二维变换中的旋转矩阵,作出了以下补充:旋转-θ角度的矩阵与旋转θ角度的转置相同,而旋转-θ角度又与旋转θ角度互为逆过程,所以我们可以得到旋转矩阵的转置等于它的逆矩阵,即旋转矩阵是正交的
1) Viewing Transformation(视图变换)
a) 什么是视图变换
一个三维虚拟世界,如何呈现在二维平面中?这一过程就是通过视图变换实现的
b) 如何表现视图变换
首先我们需要定义相机的位置、相机的朝向、以及相机朝向的正交方向

如果让相机和物体同步变换,那么我们得到的二维画面将是相同的。我们可以将相机始终放置在原点,朝向-Z方向,这时再对物体进行变换就可以得到我们需要的画面
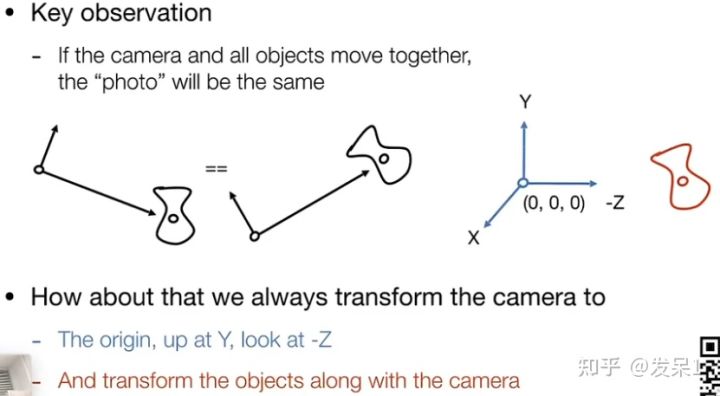
要使相机位置满足上述条件,我们需要使用如下变换
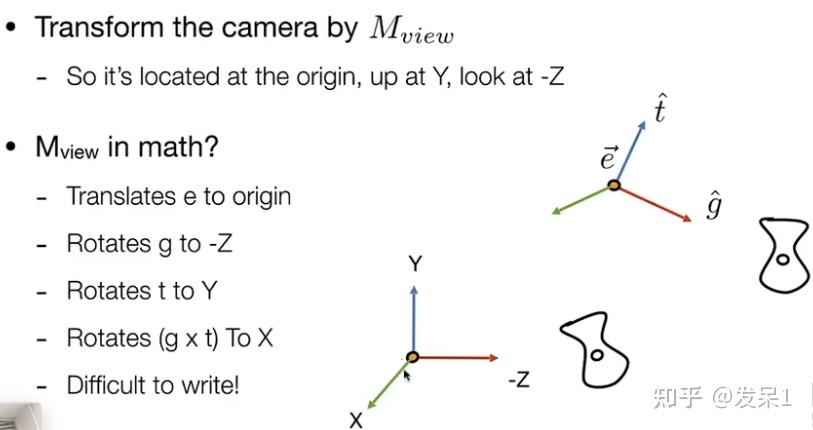
用矩阵的形式表示如下,需要注意的是在进行旋转变换时,将一个特定的方向旋转到一个规范化方向,如(0, 0, 1)比较困难,因此我们可以使用其逆变换,将一个规范化方向旋转到我们需要的方向,这样会使我们的计算方便许多,又因为旋转矩阵是正交的,我们再将所得矩阵求转置,就可得到我们需要的变换矩阵

c) 总结
视图变换也被称为模型视角变换,我们将相机移动到满足条件的位置后,再对物体和相机一同变换,就可以使物体达到我们需要的位置

2) Projection Transformation(投影变换)
a) Orthographic projection(正交投影)
正交投影可以简单的理解为:先将相机移到原点并使其满足条件,舍弃z坐标,然后将物体的坐标通过平移和缩放变换到单位坐标系中

一般来说,我们会将需要投影的长方体(相机的视野范围)映射到一个标准立方体中(先平移到原点,再进行缩放)
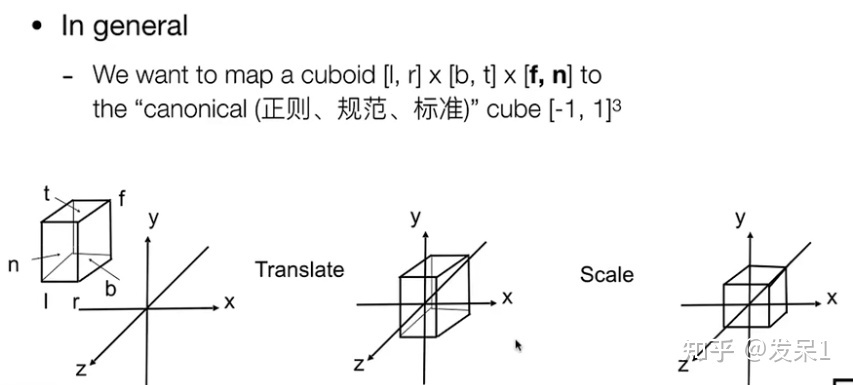
数学方式表示如下

值得注意的是,因为我们使用的是右手坐标系,由近到远是沿着-z的方向移动的,所以近处的z值会大于远处的z值,这一点同OpenGl等使用左手系不同
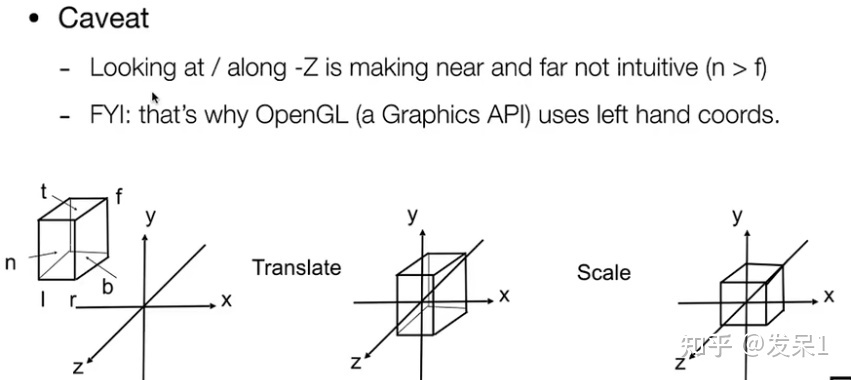
b) Perspective projection(透视投影)
透视投影中相机的视野范围是由远近平面围成的四棱台(远平面大于近平面),我们先将四棱台“挤压”成标准立方体(这一过程需要保持近平面不变,远平面z坐标不变),再进行正交投影即可
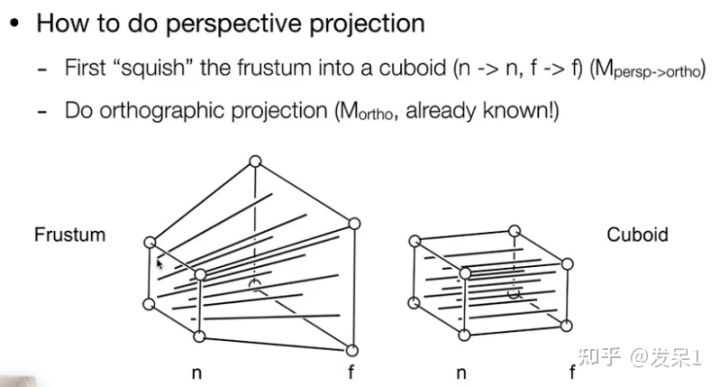
我们如何实现透视投影到正交投影的“挤压”呢?首先我们从侧面观察视锥体,可以发现远平面上的点与近平面上的点的y坐标存在一个相似三角形的关系(x坐标同理)

此时我们已经可以将变换后的坐标大概表示出来了,但是z坐标还没法得到

我们也可以大概写出这个“挤压”矩阵了,但我们仍需要求出对于z坐标的变换

思考前面提到的变换的要求:在近平面和远平面上的点在变换后z坐标均不会改变。利用这个条件我们可以对远近平面分别列出一个方程


将两个方程组成的方程组解出,我们就可以得到变换矩阵的第三行。到此,我们就完成了透视投影的推导:先通过“挤压”矩阵将视锥体变换成可以用于正交投影的标准立方体,再进行正交投影即可

至此Transformation的部分就暂时告一段落了
课程传送门:






















 6461
6461











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








