注:mubu文档转存,自学用
目录
计算方式 (从右往左) ---- right to left
-
2维变换
-
Scale
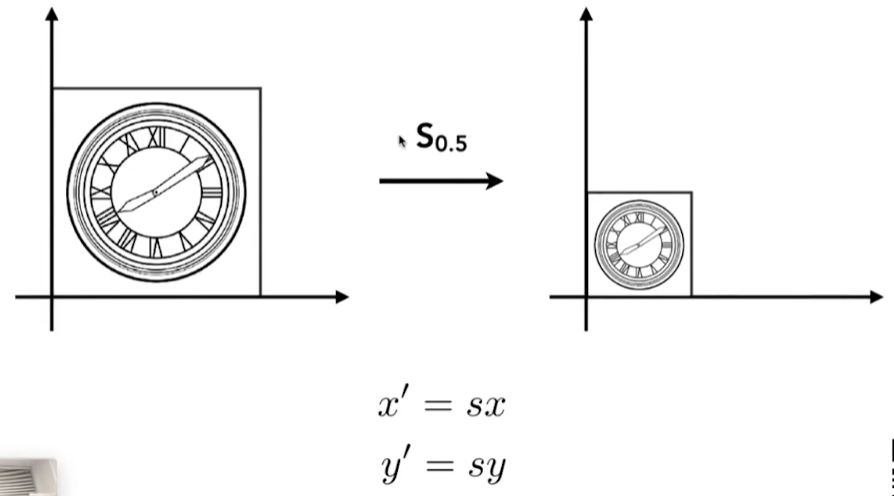
- x' - x prime
-
矩阵形式
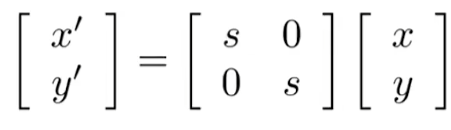
- s 为缩放矩阵
-
不均匀缩放
-
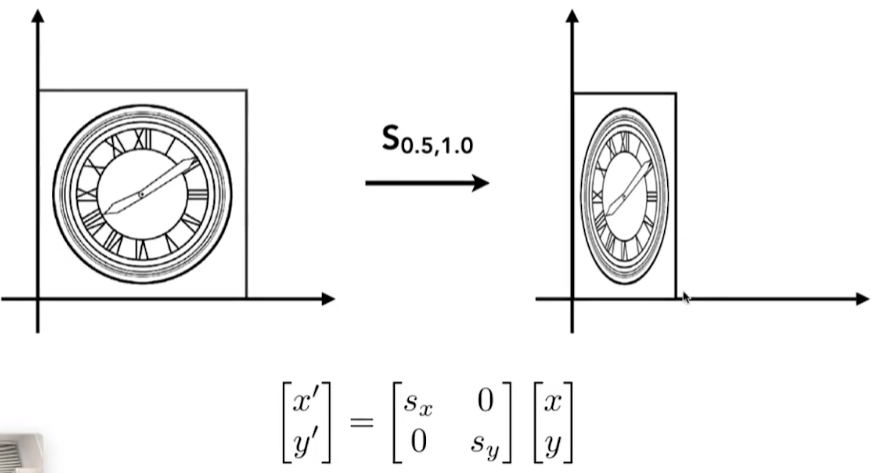
Reflection
-
Shear - 切变
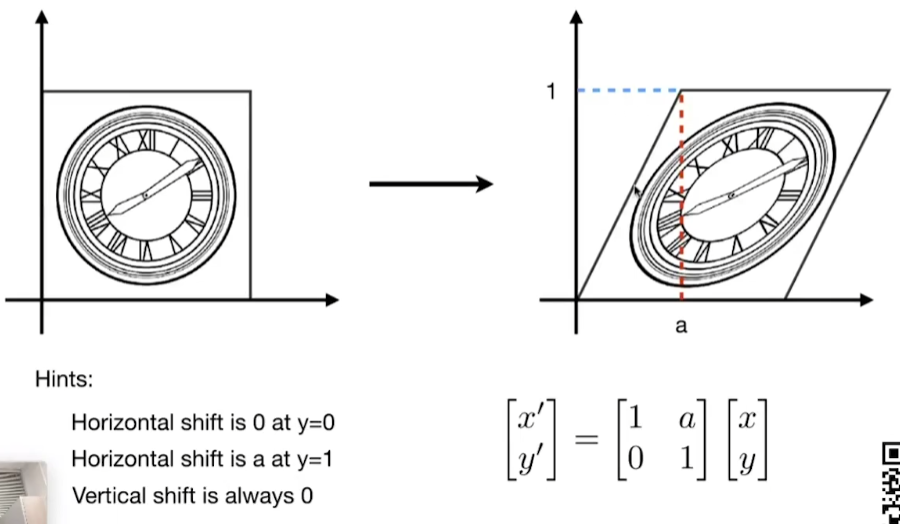
- y 不发生变化
- x 移动了 x + ay
-
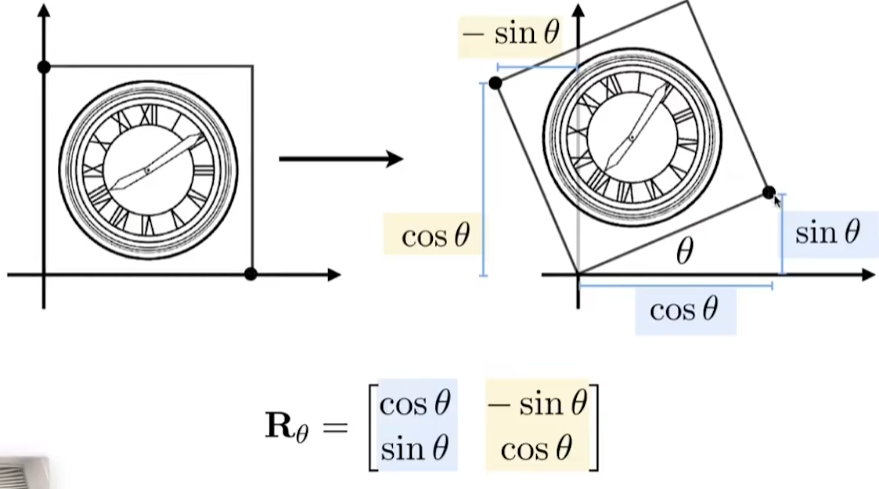
Rotate
- 默认 绕原点(0,0)进行 逆时针方向旋转
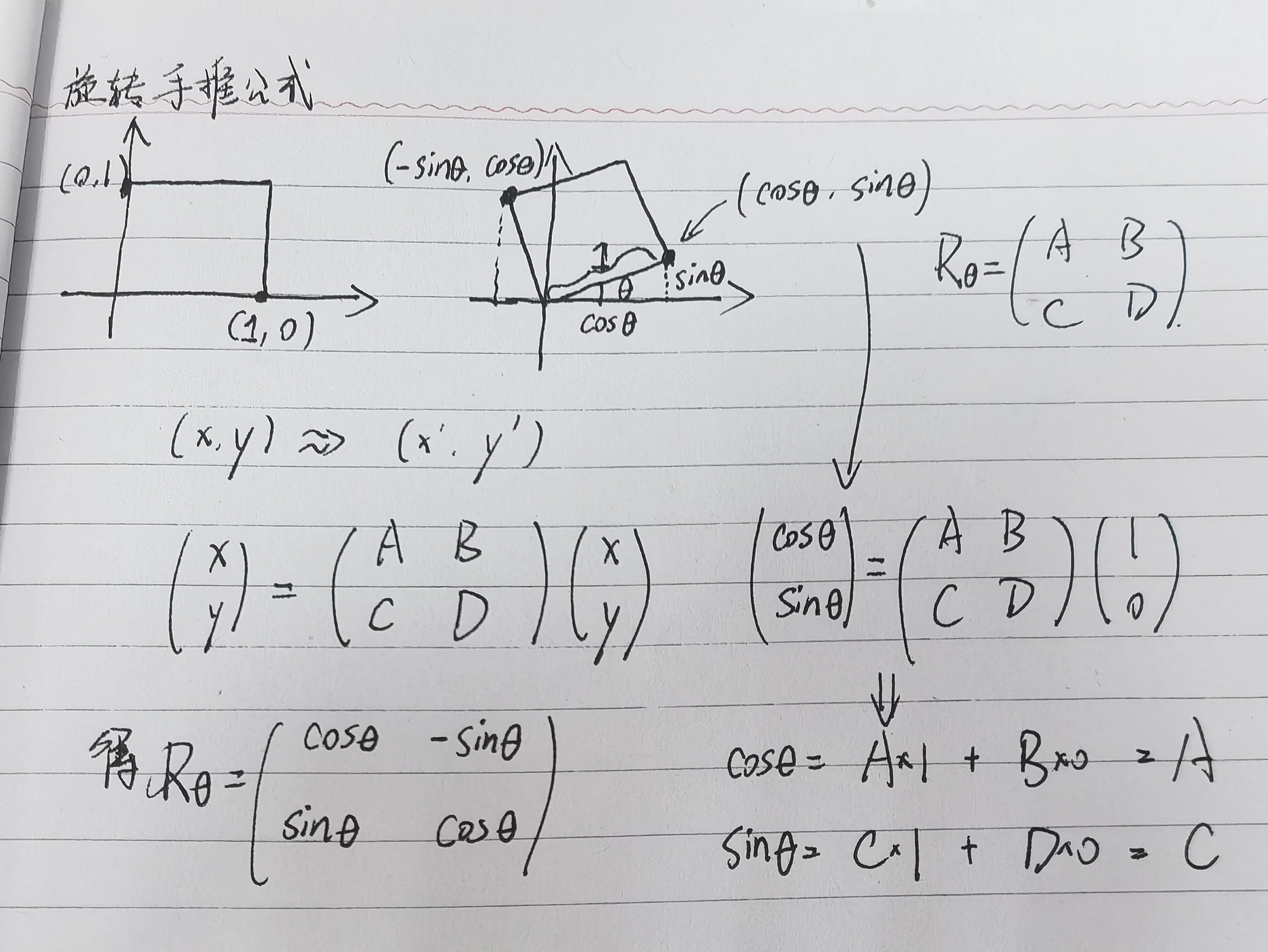
- 手推公式(2个特殊点)
- 默认 绕原点(0,0)进行 逆时针方向旋转
-
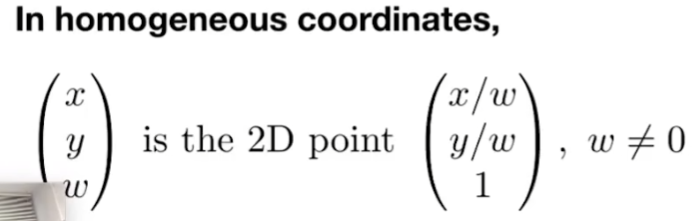
引入齐次坐标
-
线性变换
- 遵循

- 遵循
-
平移变换

- 将二维的点和向量增加了一个维度
- 向量具有平移不变性
- 同理Blender四元数运算
- 将二维的点和向量增加了一个维度
-
向量与点

- 点 + 点 = 2点的中点
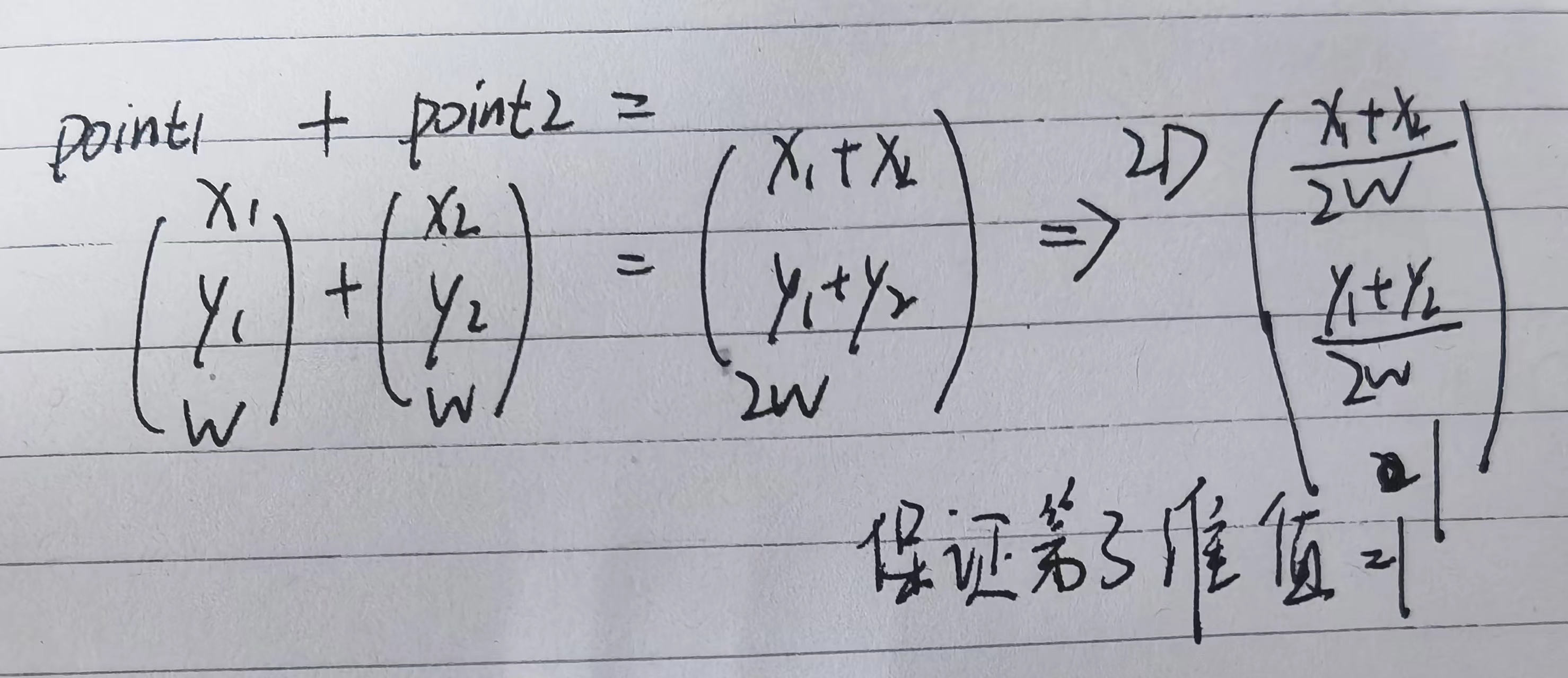
- 点 + 点 = 2点的中点
-
仿射变换
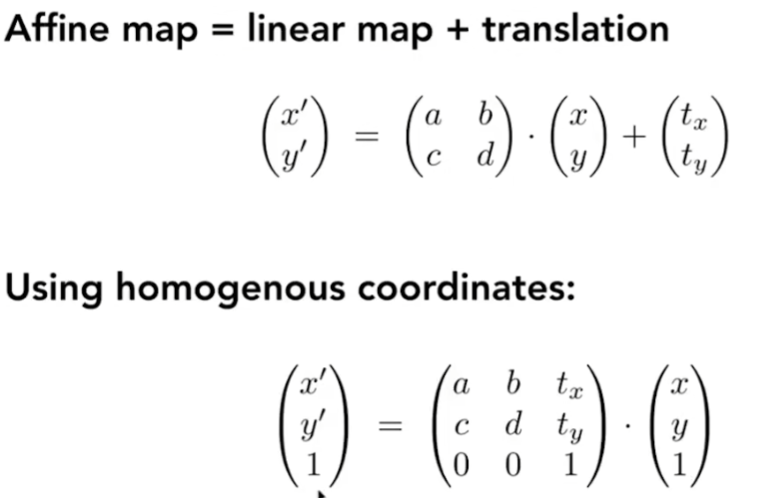
- 坐标向量化
- 矩阵最后一行的值永远是 0 0 1
- 注意点:对于 ( x , y ) 来说,变换顺序为先应用了线性变换,再应用 tx ty 的平移变换
- 在三维空间中顺序也是一样
- 缩放
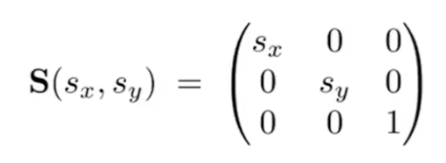
- 旋转
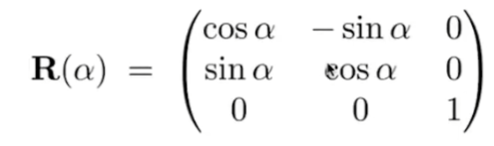
- 平移
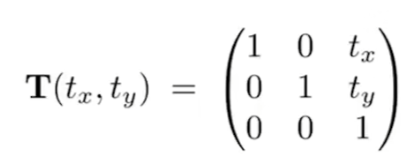
-
-
逆变换
- 定义:变换的反向操作
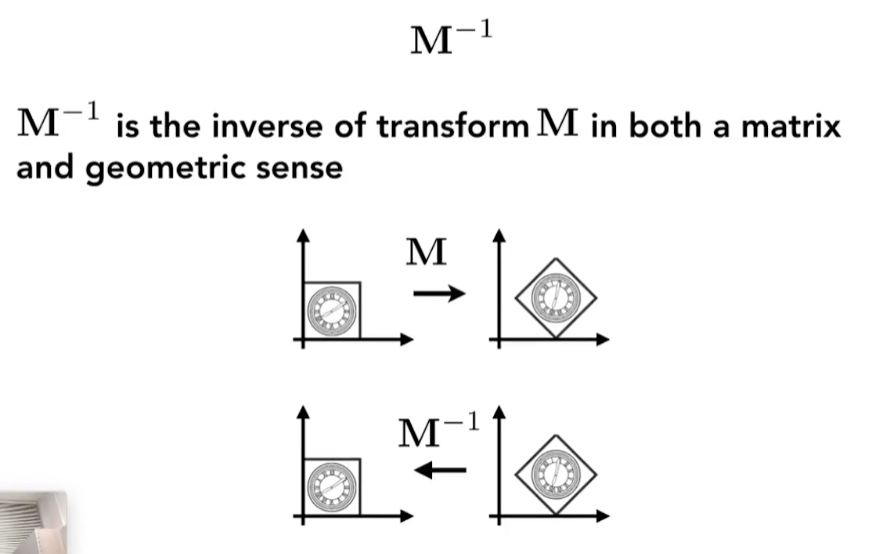
- 即是乘 逆矩阵
- 定义:变换的反向操作
-
组合变换
-
这个变换是怎么得到的?
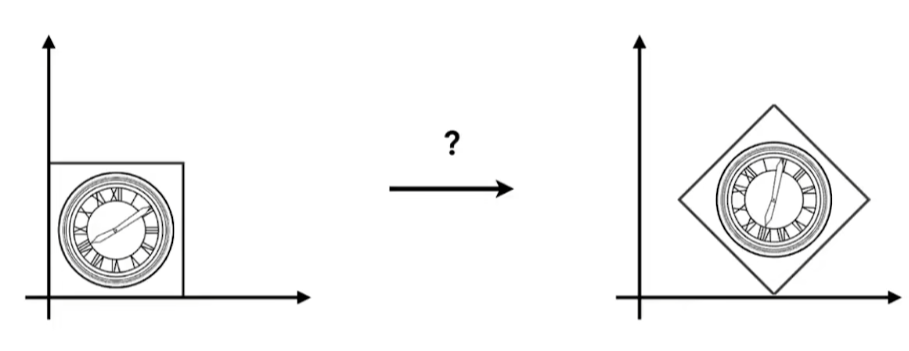
- 尝试1 ----- T(1.0) R45 为简记形式
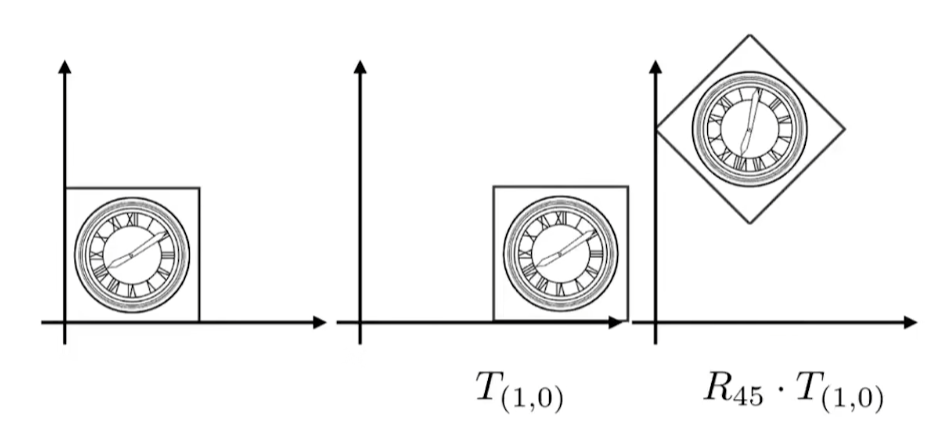
- 先平移,再默认旋转 显然不成功
- 尝试2 ---- 先旋转,再平移
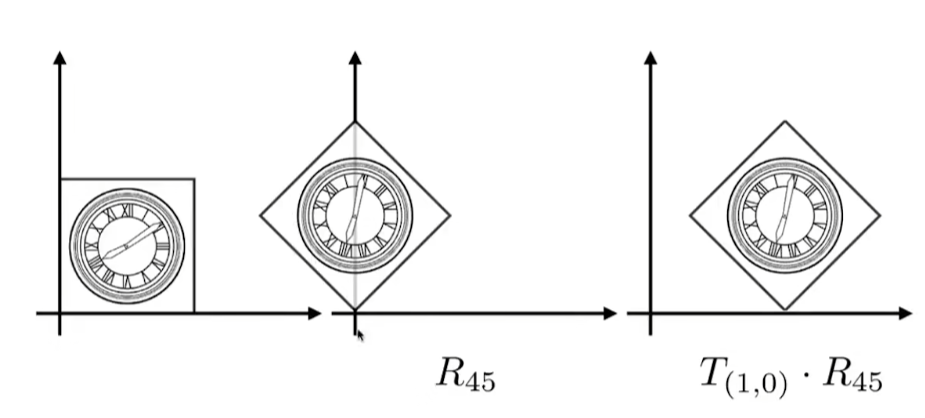
- 得到
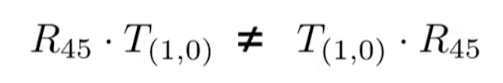
- 尝试1 ----- T(1.0) R45 为简记形式
-
结论:
- 1.复杂变换都是通过简单变换得到的
- 2.注意变换的顺序
- 理解:矩阵乘法---不满足交换律
-
计算方式 (从右往左) ---- right to left

- 先写出矩阵 [ x , y , 1 ]
- 先旋转 --- 左侧写出 R45
- 等旋转结束之后,在旋转的整体上做平移 --- 再往左边写一个 T(1,0)
-
公式性质
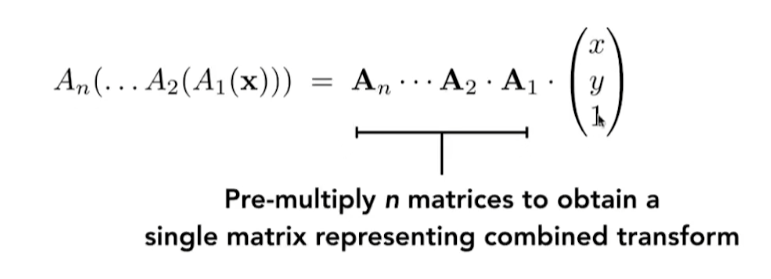
- 可以通过 结合律 节省计算量
- 3x3 的矩阵 A1.....An 相乘,最后得到的结果仍然是一个 3x3 矩阵
-
-
变换分解
- 怎样围绕 点 c 旋转,而不是默认围绕原点旋转?
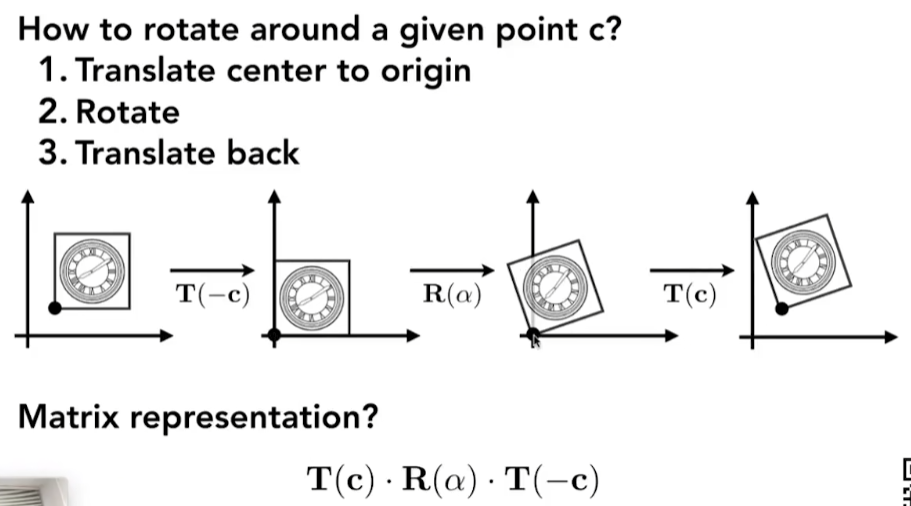
- 先将 c 点移动到原点
- 再进行 旋转操作
- 移回 c 点
- 怎样围绕 点 c 旋转,而不是默认围绕原点旋转?
-
-
3维变换
-
类比二维
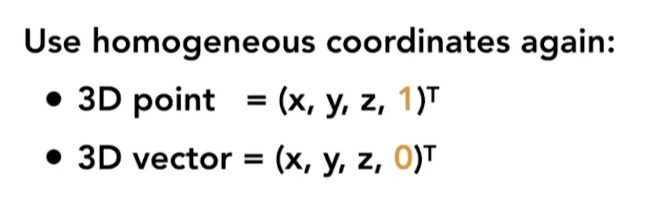
- 点 1
- 向量 0
-
齐次坐标表示
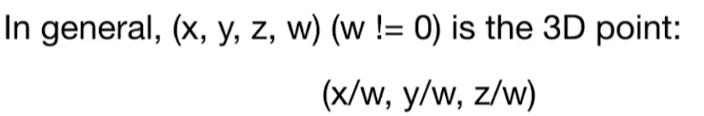
-
仿射

- 仍然是 最后一列 tx ty tz 1
- 最后一行 0 0 0 1
-
Question
- 3维变换中 先进行 线性变换 还是 先进行 平移变换?(答案在上文中)

- 3维变换中 先进行 线性变换 还是 先进行 平移变换?(答案在上文中)
-
























 579
579

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








