1️⃣ k -Means k\text{-Means} k-Means分簇方法
-
含义:一种无监督学习,用于将数据集分为 k k k个簇(每簇一个质心),使同簇点靠近/异簇点远离
-
流程:
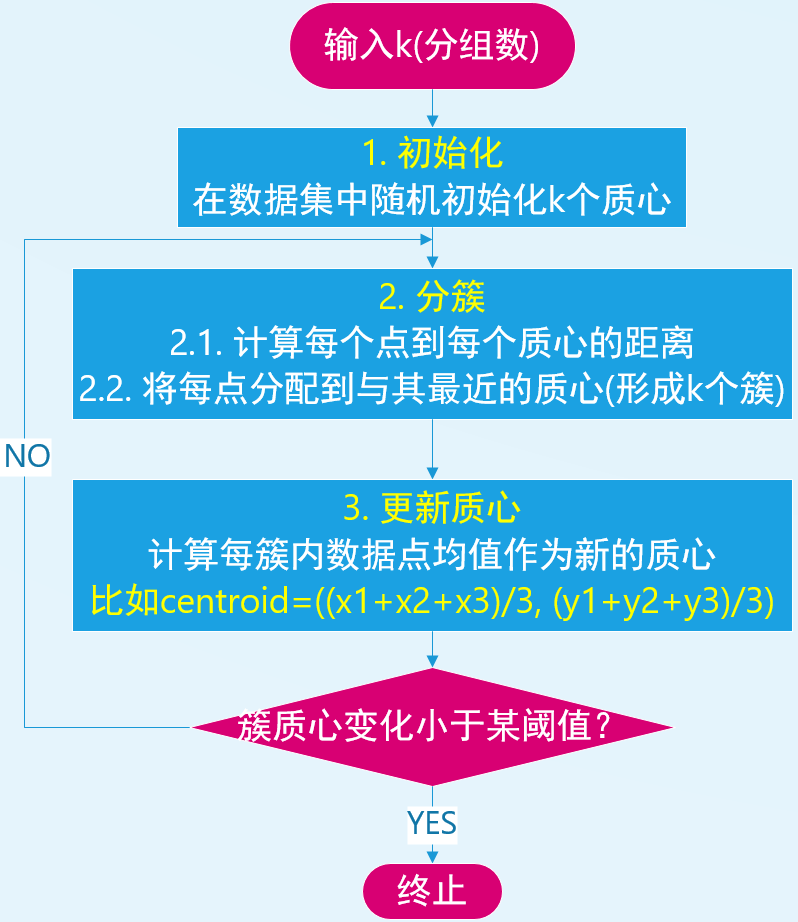
2️⃣ PQ \text{PQ} PQ算法流程
-
给定 k k k个 D D D维向量
{ v 1 = [ x 11 , x 12 , x 13 , x 14 , . . . , x 1 D ] v 2 = [ x 21 , x 22 , x 23 , x 24 , . . . , x 2 D ] . . . . . . . . . v k = [ x k 1 , x k 2 , x k 3 , x k 4 , . . . , x a D ] ↔ { v 1 = { [ x 11 , x 12 , x 13 ] , [ x 14 , x 15 , x 16 ] , . . . , [ x 1 ( D − 1 ) , x 1 ( D − 1 ) , x 1 D ] } v 2 = { [ x 21 , x 22 , x 23 ] , [ x 24 , x 25 , x 26 ] , . . . , [ x 2 ( D − 1 ) , x 2 ( D − 1 ) , x 2 D ] } . . . . . . . . . v k = { [ x k 1 , x k 2 , x k 3 ] , [ x k 4 , x k 5 , x k 6 ] , . . . , [ x k ( D − 1 ) , x k ( D − 1 ) , x k D ] } \small\begin{cases} \textbf{v}_1=[x_{11},x_{12},x_{13},x_{14},...,x_{1D}]\\\\ \textbf{v}_2=[x_{21},x_{22},x_{23},x_{24},...,x_{2D}]\\\\ \,\,\,\,\,\,\,\,\,\,\,\,.........\\\\ \textbf{v}_k=[x_{k1},x_{k2},x_{k3},x_{k4},...,x_{aD}] \end{cases}\xleftrightarrow{} \begin{cases} \textbf{v}_{1}=\{[x_{11},x_{12},x_{13}],[x_{14},x_{15},x_{16}],...,[x_{1(D-1)},x_{1(D-1)},x_{1D}]\}\\\\ \textbf{v}_{2}=\{[x_{21},x_{22},x_{23}],[x_{24},x_{25},x_{26}],...,[x_{2(D-1)},x_{2(D-1)},x_{2D}]\}\\\\ \,\,\,\,\,\,\,\,\,\,\,\,.........\\\\ \textbf{v}_{k}=\{[x_{k1},x_{k2},x_{k3}],[x_{k4},x_{k5},x_{k6}],...,[x_{k(D-1)},x_{k(D-1)},x_{kD}]\} \end{cases} ⎩ ⎨ ⎧v1=[x11,x12,x13,x14,...,x1D]v2=[x21,x22,x23,x24,...,x2D].........vk=[xk1,xk2,xk3,xk4,...,xaD] ⎩ ⎨ ⎧v1={[x11,x12,x13],[x14,x15,x16],...,[x1(D−1),x1(D−1),x1D]}v2={[x21,x22,x23],[x24,x25,x26],...,[x2(D−1),x2(D−1),x2D]}.........vk={[xk1,xk2,xk3],[xk4,xk5,xk6],...,[xk(D−1),xk(D−1),xkD]}
-
分割子空间:将 D D D维向量分为 M M M个 D M \cfrac{D}{M} MD维向量
子空间 1 { v 11 = [ x 11 , x 12 , x 13 ] v 21 = [ x 21 , x 22 , x 23 ] . . . . . . . . . v k 1 = [ x k 1 , x k 2 , x k 3 ] & 子空间 2 { v 12 = [ x 14 , x 15 , x 16 ] v 22 = [ x 24 , x 25 , x 26 ] . . . . . . . . . v k 2 = [ x k 4 , x k 5 , x k 6 ] & . . . & 子空间 M { v 1 M = [ x 1 ( D − 1 ) , x 1 ( D − 1 ) , x 1 D ] v 2 M = [ x 2 ( D − 1 ) , x 2 ( D − 1 ) , x 2 D ] . . . . . . . . . v k M = [ x k ( D − 1 ) , x k ( D − 1 ) , x k D ] \small子空间1\begin{cases} \textbf{v}_{11}=[x_{11},x_{12},x_{13}]\\\\ \textbf{v}_{21}=[x_{21},x_{22},x_{23}]\\\\ \,\,\,\,\,\,\,\,\,\,\,\,.........\\\\ \textbf{v}_{k1}=[x_{k1},x_{k2},x_{k3}] \end{cases}\&子空间2 \begin{cases} \textbf{v}_{12}=[x_{14},x_{15},x_{16}]\\\\ \textbf{v}_{22}=[x_{24},x_{25},x_{26}]\\\\ \,\,\,\,\,\,\,\,\,\,\,\,.........\\\\ \textbf{v}_{k2}=[x_{k4},x_{k5},x_{k6}] \end{cases}\&...\&子空间M \begin{cases} \textbf{v}_{1M}=[x_{1(D-1)},x_{1(D-1)},x_{1D}]\\\\ \textbf{v}_{2M}=[x_{2(D-1)},x_{2(D-1)},x_{2D}]\\\\ \,\,\,\,\,\,\,\,\,\,\,\,.........\\\\ \textbf{v}_{kM}=[x_{k(D-1)},x_{k(D-1)},x_{kD}] \end{cases} 子空间1⎩ ⎨ ⎧v11=[x11,x12,x13]v21=[x21,x22,x23].........vk1=[xk1,xk2,xk3]&子空间2⎩ ⎨ ⎧v12=[x14,x15,x16]v22=[x24,x25,x26].........vk2=[xk4,xk5,xk6]&...&子空间M⎩ ⎨ ⎧v1M=[x1(D−1),x1(D−1),x1D]v2M=[x2(D−1),x2(D−1),x2D].........vkM=[xk(D−1),xk(D−1),xkD]
-
生成 PQ \text{PQ} PQ编码:
子空间 1 { v 11 ← 替代 Centriod 11 v 21 ← 替代 Centriod 21 . . . . . . . . . v k 1 ← 替代 Centriod k 1 & 子空间 2 { v 12 ← 替代 Centriod 12 v 22 ← 替代 Centriod 22 . . . . . . . . . v k 2 ← 替代 Centriod k 2 & . . . & 子空间 M { v 1 M ← 替代 Centriod 1 M v 2 M ← 替代 Centriod 2 M . . . . . . . . . v k M ← 替代 Centriod k M \small子空间1\begin{cases} \textbf{v}_{11}\xleftarrow{替代}\text{Centriod}_{11}\\\\ \textbf{v}_{21}\xleftarrow{替代}\text{Centriod}_{21}\\\\ \,\,\,\,\,\,\,\,\,\,\,\,.........\\\\ \textbf{v}_{k1}\xleftarrow{替代}\text{Centriod}_{k1} \end{cases}\&子空间2 \begin{cases} \textbf{v}_{12}\xleftarrow{替代}\text{Centriod}_{12}\\\\ \textbf{v}_{22}\xleftarrow{替代}\text{Centriod}_{22}\\\\ \,\,\,\,\,\,\,\,\,\,\,\,.........\\\\ \textbf{v}_{k2}\xleftarrow{替代}\text{Centriod}_{k2} \end{cases}\&...\&子空间M \begin{cases} \textbf{v}_{1M}\xleftarrow{替代}\text{Centriod}_{1M}\\\\ \textbf{v}_{2M}\xleftarrow{替代}\text{Centriod}_{2M}\\\\ \,\,\,\,\,\,\,\,\,\,\,\,.........\\\\ \textbf{v}_{kM}\xleftarrow{替代}\text{Centriod}_{kM} \end{cases} 子空间1⎩ ⎨ ⎧v11替代Centriod11v21替代Centriod21.........vk1替代Centriodk1&子空间2⎩ ⎨ ⎧v12替代Centriod12v22替代Centriod22.........vk2替代Centriodk2&...&子空间M⎩ ⎨ ⎧v1M替代Centriod1Mv2M替代Centriod2M.........vkM替代CentriodkM
-
聚类:在每个子空间上运行 k -Means k\text{-Means} k-Means算法(一般 k = 256 k\text{=}256 k=256) → \to →每个 v i j \textbf{v}_{ij} vij都会分到一个 D M \cfrac{D}{M} MD维的质心
-
编码:将每个子向量 v i j \textbf{v}_{ij} vij所属质心的索引作为其 PQ \text{PQ} PQ编码,并替代原有子向量
-
-
生成最终的压缩向量 → { v 1 ~ = { Centriod 11 , Centriod 12 , . . . , Centriod 1 M } v 2 ~ = { Centriod 21 , Centriod 22 , . . . , Centriod 2 M } . . . . . . . . . v k ~ = { Centriod k 1 , Centriod k 2 , . . . , Centriod k M } \small\to\begin{cases} \widetilde{\textbf{v}_{1}}=\{\text{Centriod}_{11},\text{Centriod}_{12},...,\text{Centriod}_{1M}\}\\\\ \widetilde{\textbf{v}_{2}}=\{\text{Centriod}_{21},\text{Centriod}_{22},...,\text{Centriod}_{2M}\}\\\\ \,\,\,\,\,\,\,\,\,\,\,\,.........\\\\ \widetilde{\textbf{v}_{k}}=\{\text{Centriod}_{k1},\text{Centriod}_{k2},...,\text{Centriod}_{kM}\} \end{cases} →⎩ ⎨ ⎧v1 ={Centriod11,Centriod12,...,Centriod1M}v2 ={Centriod21,Centriod22,...,Centriod2M}.........vk ={Centriodk1,Centriodk2,...,CentriodkM}
- 存储阶段:存储的内容实质上是质心索引,每个向量只占用 M M M维
- 使用阶段:所有的质心索引被解压为质心,每个向量维度又恢复 M × D M = D M\text{×}\cfrac{D}{M}\text{=}D M×MD=D维
3️⃣ IVF+PQ \text{IVF+PQ} IVF+PQ原理
- 离线索引阶段:
- 构建 IVF \text{IVF} IVF:使用 K-Menas \text{K-Menas} K-Menas将原始向量集合划分为 n n n簇(即 n n n个质心)
- 簇内压缩:对每个簇执行 PQ \text{PQ} PQ压缩,即将每个簇内向量替换为质心索引
- 在线查询阶段:
- IVF \text{IVF} IVF部分:计算与查询 q q q与所有簇质心的距离,由此选定前 n probe n_{\text{probe}} nprobe个簇的所有向量
- PQ \text{PQ} PQ部分:由质心索引还原选定向量 → \text{→} →计算 q q q之的距离(遍历子空间) dist ( q , v ) ≈ ∑ i = 1 M dist ( q i , c j i ) → \displaystyle{}\text{dist}(q, v) \text{≈} \sum_{i=1}^M \text{dist}\left(q_i, c_{j i}\right)\text{→} dist(q,v)≈i=1∑Mdist(qi,cji)→返回最近邻























 725
725

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








